Основные сведения из термодинамики

Как было сказано выше, выстрел представляет собой сложный термодинамический и газодинамический процесс очень быстрого превращения химической энергии пороха сначала в тепловую, а затем в механическую работу перемещенbz снаряда, откатных частей орудия и заряда. Орудие можно рассматривать как тепловую машину. Ниже приводятся основные сведения из термодинамики применительно к выстрелу.

Энергией тела называется его способность совершать работу.

Термодинамика – наука, занимающаяся изучением законов превращения энергии, при котором происходит изменение температуры участвующих в процессе тел, обмен тепла между ними и совершение механической работы.

Превращение тепловой энергии в механическую в тепловой машине (двигателе) совершается при помощи промежуточного тела, которое называется рабочим телом. Большей частью рабочим телом служит газ, например, пороховые газы.

Газ характеризуется величинами, которые носят название параметров состояния. К параметрам состояния относятся: давление, удельный объем, удельный вес и температура.

Давление – р – сила, действующая по нормали со стороны газа на единицу площади поверхности оболочки. Согласно кинетической теории вещества давление газа р численно равно 2/3 кинетической энергии поступательного движения молекул, заключенных в единице объема.

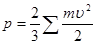(2.1.)

где m – масса газов, v скорость молекул газов.

В артиллерийской технике давление газа измеряется в кг/см² или кг/дм².

Удельный объем – w - объем, занимаемый единицей веса вещества.

, дм³/ кг (2.2.)

где W – объем, ω – вес вещества

Удельный вес – γ – вес единицы объема. Величина его обратна удельному объему.

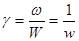, кг/дм³ (2.3.)

Иногда вместо удельного веса γ пользуются массовой плотностью газа, она равна

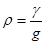(2.4.)

где g – ускорение силы тяжести, равное 98,1 дм/сек².

Температура представляет собой степень нагретости тела и выражается в градусах или по стоградусной шкале Цельсия (t ºC) или по абсолютной шкале (Т К), связь между ними имеет вид

Т К = 273 º + t ºC (2.5.)

За рубежом используется шкала Фаренгейта (F). Перевод температуры по шкале Фаренгейта (Цельсия (t ºф) в температуру по шкале Цельсия (t ºС) осуществляется по формуле

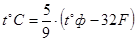(2.6.)

Термическое уравнение состояния газа – это фундаментальная связь между параметрами состояния газа. Оно имеет вид:

F = (р, w, Т) = 0 или р = ƒ₁ (w, Т), Т = ƒ₂ (р₁ w), w = ƒ₃ (р₁ Т)

Как известно, в физике различают два вида газов: идеальные и реальные

Идеальным называют газ, молекулы которого не имеют объема и лишены сил взаимодействия. Для него уравнение состояния имеет вид:

р · w = R T (2.7.)

Которое называется уравнением Клайперона и где R – газовая постоянная. Для произвольного объема уравнение (2.7.) имеет вид

p W = ω R T (2.8.)

Газовую постоянную R можно определить , зная удельный объем w, при атмосферном давлении и 0 ºС

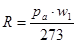
где p_a = 103,3 кг/дм²

Для пороховых газов, имеющих w₁ = 800 – 1000 дм³/кг

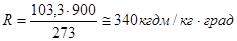
Газовая постоянная R представляет собой работу, совершаемую 1 кг данного газа, расширяющегося под постоянным давлением при нагревании на 1 ºС.

Если в уравнении (2.8.) принять вес газа ω равным молекулярному весу – μ, уравнение примет вид:

p ·W_μ = μ R T = R_μ · Т (2.9.)

Где W_μ объем 1 моля газа

R_μ = μ · R – универсальная газовая постоянная

Согласно закона Авогадро объем молей всех идеальных газов W_μ при одинаковых температурах и давлениях одинаковы. При р = р_а и Т = 273 К, W_μ = 22,4 г/дм³ = 22400 кг/дм³. Тогда

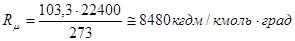
Ввиду того, что R_μ = μ · R, значение R для данного газа можно получить, зная молекулярный вес газа.

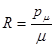
Практика показала, что связь между параметрами состояния реальных газов уклоняется от уравнения состояния идеальных газов. Имеется много различных формул для учета взаимодействия молекул и их собственного объема, например, уравнение Ван дер Ваальса:

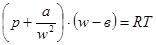(2.10.)

где: “а” и “в” – постоянные для данного газа;

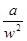– поправка, учитывающая силы взаимодействия молекул;

в – поправка, учитывающая собственный объем молекул. Во внутренней баллистики она носит название коволюма и обозначается буквой α.

При высоких температурах газа, например, при выстреле, величина 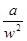мала и ею можно пренебречь.

В таком случае уравнение состояния реального газа можно представить в виде:

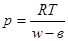(2.11.)

Газ, подчиняющийся этому состоянию носит название газ Дюпре.