Додавання і віднімання синусоїдних функцій часу на комплексній площині

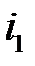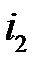Припустимо, що необхідно додати два струми ( і ) однакової частоти. Сума їх дає деякий струм з тією ж частотою:

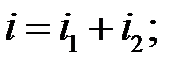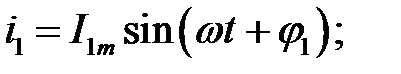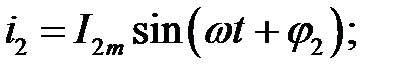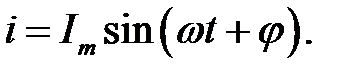Необхідно знайти амплітуду 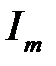і початкову фазу 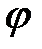струму 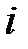. З цією ціллю струм 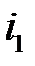зобразимо на комплексній площині (рис. 25.1) вектором 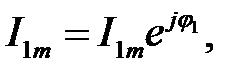а струм 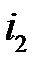– вектором 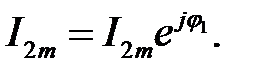Геометрична сума векторів 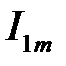і 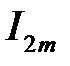дає комплексну амплітуду сумарного струму 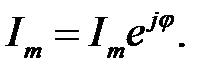Амплітуда струму 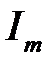знаходиться за довжиною сумарного вектора, а початкова фаза – кутом, утвореним цим вектором і віссю +1.

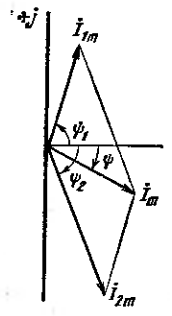
Рис. 25.1

Для знаходження різниці двох струмів (е.р.с., напруги) необхідно навколо початку координат провезти не додавання, а віднімання відповідних векторів.

Звернемо увагу на те, що якби вектори 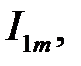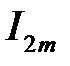і 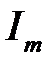стали обертатися довкола початку координат з кутовою швидкістю 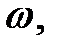то взаємне розташування векторів по відношенню одне до одного залишилось би без змін.

Векторна діаграма

Векторною діаграмою називається сукупність векторів на комплексній площині, що зображують синусоїдально змінні функції часу однієї і тієї ж частоти і побудовані з дотриманням правильної орієнтації їх одна відносно іншої по фазі. Приклад векторної діаграми даний на рис. 26.1.

Рис. 26.1

Миттєва потужність в колах синусоїдного струму

Протікання синусоїдальних струмів по ділянках електричного кола супроводжується споживанням енергії від джерел. Швидкість надходження енергії характеризується потужністю. Під миттєвим значенням потужності, або під миттєвою потужністю, розуміють добуток миттєвого значення напруги 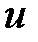на ділянці кола на миттєве значення струму 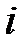, що протікає по цій ділянці:

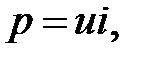(27.1)

де 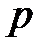– функція часу.

Резистор в колі синусоїдного струму.

На рис. 28.1, а зображено активний опір 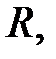по якому протікає струм 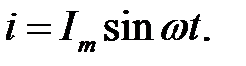За законом Ома, напруга

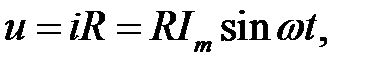або

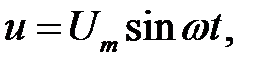(28.1)

де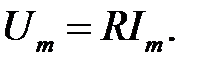

Комплекс струму 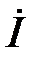і співпадаючий з ним по фазі комплекс напруги показані на векторній діаграмі рис. 28.1, б.

На рис. 28.1, в дані криві миттєвих значень струму 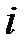, напруги 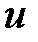і потужності

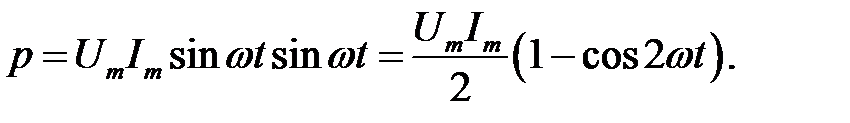Миттєва потужність має постійну складову 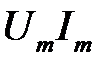і складову 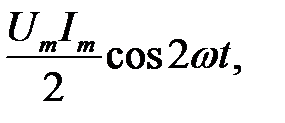яка змінюється з частотою 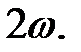Спожита від джерела живлення за час 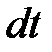енергія рівна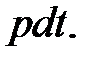

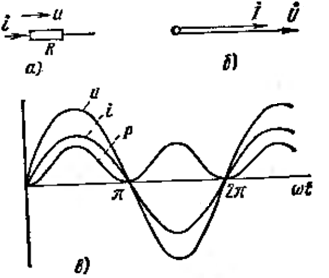
Рис. 28.1

Індуктивна котушка в колі синусоїдного струму

Практично будь-яка обмотка (котушка) володіє деякою індуктивністю 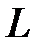і активним опором 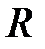. На схемі котушку можна представити у вигляді послідовного з’єднання індуктивності 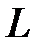і активного опору .

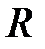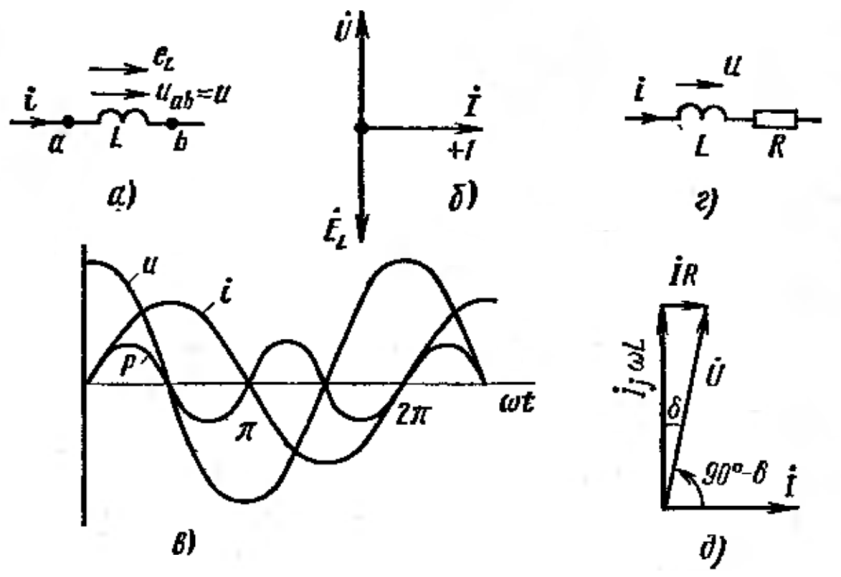
Рис. 29.1

Виділимо із схеми одну індуктивність 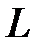(без активного опору) – рис. 29.1, а. Якщо через 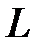протікає струм 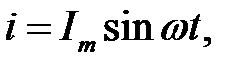тоді в котушці наводиться е.р.с. самоіндукції

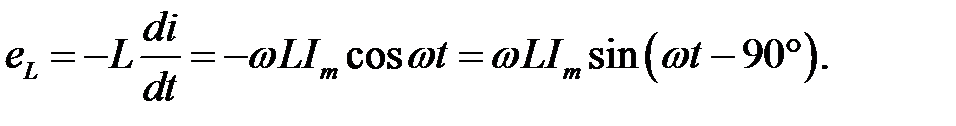Додатній напрям відліку для е.р.с. 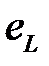на рис. 29.1, а позначено стрілкою, яка співпадає з додатнім напрямом відліку струму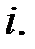

Знайдемо різницю потенціалів між точками а і b.

При переміщенні від точки b до точки а йдемо на зустріч е.р.с. 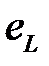, тому 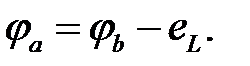Відповідно,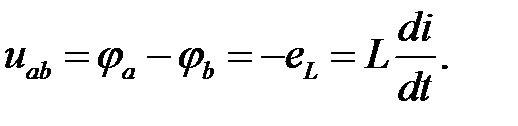

Додатній напрям напруги 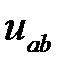співпадає з додатнім напрямом струму.

В подальшому індекси а і b коло напруги на індуктивності (спад напруги на індуктивності) ставити не будемо:

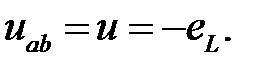(29.1)

Відповідно

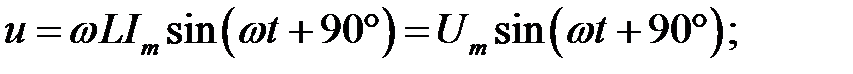(29.2)

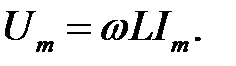Добуток 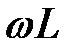позначається 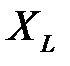і називається індуктивним опором:

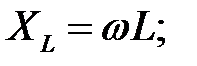(29.3)

його розмірність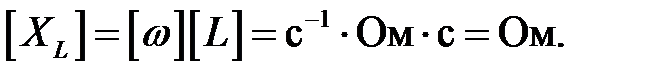

Таким чином, індуктивність створює змінному струму опір, модуль якого 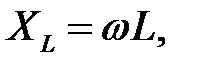прямо пропорційний частоті. Крім того, напруга на індуктивності випереджає струм по фазі на 90° – на рис. 29.1, б вектор напруги випереджає вектор струму 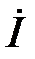на 90°. Комплекс е.р.с. самоіндукції 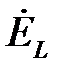знаходиться в протифазі з комплексом напруги .

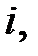
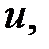
Графік миттєвих значень 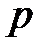зображені на рис. 29.1, в.

Миттєва потужність

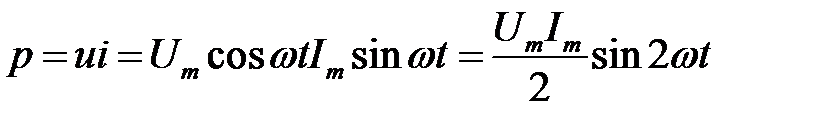(29.4)

Проходить через нульове значення, коли через нуль проходить 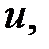або або 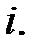За першу чверть періоду, коли 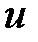і 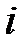додаткові, 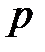також додаткова. Площа, що обмежена кривою 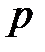і віссю абсцис за цей час, являє собою енергію, яка взята від джерела живлення на створення енергії магнітного поля в індуктивності. В другій четверті періоду, коли струм у колі зменшується від максимуму до нуля, енергія магнітного поля віддає назад джерелу живлення, при цьому миттєва потужність від’ємна. За третю чверть періоду в джерела живлення забирається енергія, за четверту віддається і так далі, тобто енергія періодично то забирається індуктивністю від джерела, то віддається йому назад.

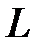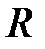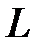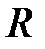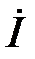Реальна індуктивна котушка крім індуктивності володіє і активним опором (рис. 29.1, г). Тому спад напруги на реальній індуктивній котушці рівний сумі напруг на і на (рис. 29.1, д). Як видно з цього рисунку, кут між напругою на котушці і струмом рівний 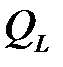причому 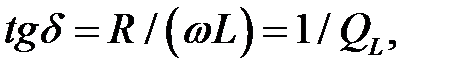де 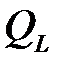– добротність реальної котушки. Чим більше 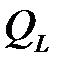, тим менший кут