Класифікація функцій одного аргументу

1. Ціла раціональна функція або многочлен.

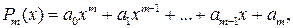
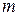–ціле, 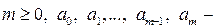сталі (дії, за допомогою яких формується многочлен: додавання, віднімання, множення, піднесення до цілого додатнього степеня).

2. Дробова-раціональна функція

.

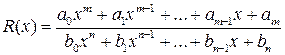(крім перелічених чотирьох дій при формуванні 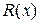, використовується дія ділення)

1.+ 2. 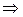раціональні функції.

3. Ірраціональна функція (при її формуванні до перелічених дій додається дія добування кореня).

Наприклад, .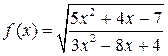

(1.+ 2.) + 3. 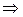явні алгебраїчні функції.

4. Трансцендентні функції – усякі неалгебраїчні функції.

Найпростіші (елементарні) трансцендентні функції:

а) показникова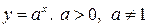

б) логарифмічна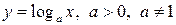

в) тригонометричні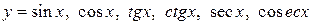

г) обернені тригонометричні функції .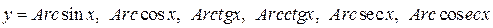

Функції алгебраїчні, елементарні трансцендентні і їх комбінації називаються елементарні функції.

Поняття зложеної (складеної) функції.

Нехай 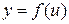, а аргумент 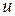у свою чергу є деяка функція від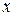 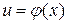. Тоді, зрештою, 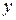буде функцією від 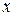, яка називається зложеною функцією, або складеною, або функцією від функції.

.

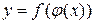Приклади: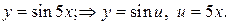

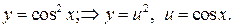
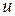– проміжний аргумент. Зложену функцію можна утворити не тільки з 2-х функцій:

,

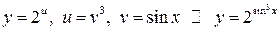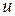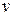і – проміжні аргументи.

Границя функції

Поняття границі функції – одне з найважливіших у вищій математиці.

Нехай на деякій множині Χ визначена функція .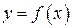

Означення. Число А називається границею функції 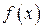при 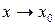(або у точці 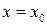), якщо для будь-якого ε > 0 можна знайти таке число 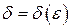> 0, що при всіх 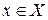, які задовольняють нерівність

0 < < ,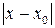

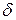виконується нерівність

< .

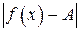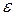Приклад 1. Покажемо, що функція 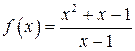має в точці 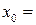0 границю, яка дорівнює 1.

Щоб це довести, ми повинні згідно з означенням для довільного ε > 0 вказати таке δ > 0, при якому із нерівності 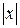< δ випливала б нерівність

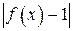< ε.

Розглянемо 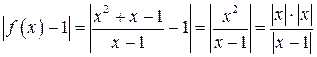< 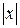, оскільки 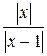<1.

Отже, оскільки 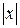< δ, то 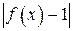буде менше, ніж будь-яке ε > 0, досить δ взяти меншим, ніж ε: 0 < δ < ε.

Таким чином нерівність

<

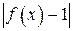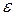
виконується завжди для δ < ε. Тоді згідно з означенням .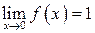

Насправді визначення границі рідко використовується при обчисленні границь.

Приклад 2. Знайти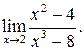

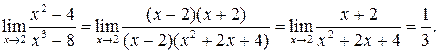
Приклад 3. Знайти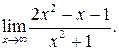

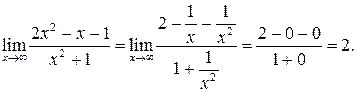
Існують дві визначальні границі:

1.

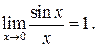
2.

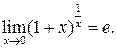
Приклад 4. Знайти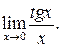

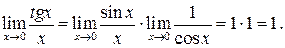
Приклад 5. Знайти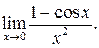

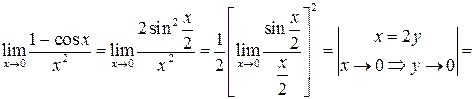
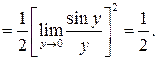
Приклад 6. Знайти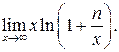

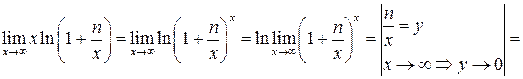
Функція 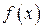називається неперервною в точці 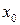, якщо границя функції дорівнює її значенню в цій точці, тобто:

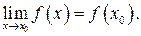(1)

Точка 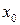називається точкою розриву функції 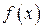, якщо 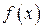у точці 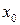не є неперервною. Таким чином, у точках розриву функція не визначена.

Якщо функція 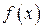неперервна на 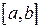, тоді вона досягає на цьому відрізку свого найбільшого і найменшого значення, тобто 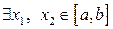, що (за теоремою Вейєрштрасса)

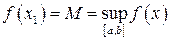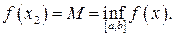і (2)