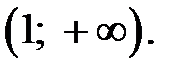Определение 15. Пусть функция 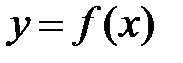 определена на множестве D. Если для любых значений аргументов
определена на множестве D. Если для любых значений аргументов 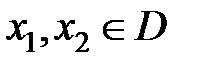 из неравенства
из неравенства 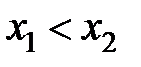 вытекает неравенство
вытекает неравенство 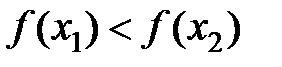 , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве
| Рис.7. Интервалы монотонности |
D; если
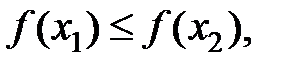
то функция называется неубывающей на множествеD; если
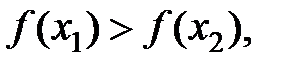
то функция называется убывающей на множествеD; при
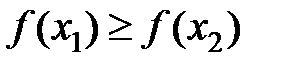
функция называется невозрастающей на множествеD.
Определение 16. Убывающие, возрастающие, невозрастающие, неубывающие функции на множестве D называются монотонными на этом множестве, а убывающие и возрастающие − строго монотонными.
Определение 17. Интервалы, в которых функция монотонна, называются интервалами монотонности.
Например, графически заданная функция 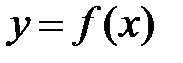 (рис. 7) убывает на интервале (-2;1) (строго монотонна), не убывает на интервале (1;5) (монотонна), возрастает на интервале (3;5) (строго монотонна).
(рис. 7) убывает на интервале (-2;1) (строго монотонна), не убывает на интервале (1;5) (монотонна), возрастает на интервале (3;5) (строго монотонна).
Теорема 5 (необходимые условия возрастания (убывания) функции). Если дифференцируемая на интервале 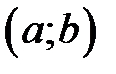 функция
функция 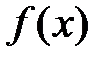 возрастает (убывает), то
возрастает (убывает), то 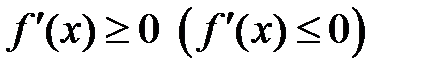 для любых
для любых 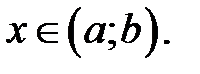
Теорема6 (достаточные условия возрастания (убывания) функции). Если функция 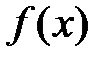 дифференцируема на интервале
дифференцируема на интервале 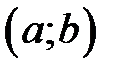 и
и 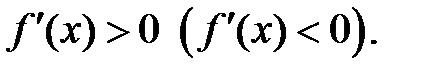 для любых
для любых 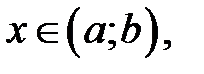 то эта функция возрастает (убывает) на интервале
то эта функция возрастает (убывает) на интервале 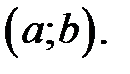
| Рис. 8. Касательные к графикам возрастающей и убывающей функций |
Геометрически условия монотонности означают: если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс, то функция возрастает (рис.8, а), если под тупыми, то убывает (рис.8, б).
Определение 18. Пусть функция 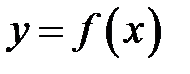 определена в точке
определена в точке 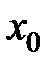 и в некоторой окрестности этой точки.Точка
и в некоторой окрестности этой точки.Точка 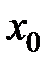 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 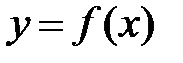 , если существует такая
, если существует такая 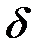 -окрестность точки
-окрестность точки 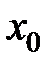 , что для всех
, что для всех 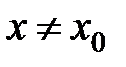 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 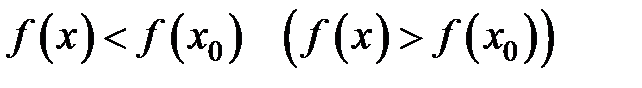 (рис. 9а, б; рис. 10).
(рис. 9а, б; рис. 10).
Определение 19. Точки максимума и минимума называются экстремальными точками (экстремумами).
Определение 20. Значение функции в точках максимума (минимума) называется максимумом (минимумом) функции − экстремумом функции.
Экстремумфункциичасто называют локальным экстремумом, подчеркивая тот факт, что понятие экстремумасвязано лишь с достаточно малой 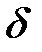 -окрестностью точки
-окрестностью точки 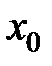 . Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой точке. Наличие максимума (минимума) в отдельной точке данного промежутка вовсе не означает, что в этой точке функция
. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой точке. Наличие максимума (минимума) в отдельной точке данного промежутка вовсе не означает, что в этой точке функция 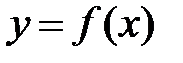 принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)). В данномучебно-методическом пособии мы будем рассматривать только локальные экстремумы.
принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)). В данномучебно-методическом пособии мы будем рассматривать только локальные экстремумы.
Теорема 7 (необходимое условие экстремума). Если
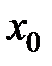
− точка локального экстремума для функции
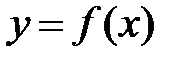
, то в этой точке производная функции либо равна (
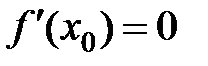
),либо не существует.
| Рис. 9. Касательная, параллельная Ох |
| Рис. 10. Касательная в точках экстремума |
Геометрически теорема означает, что в точках экстремума касательная к графику функции либо параллельна оси Ох (если
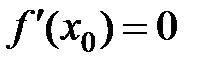
) (см. рис. 9,а, б), либо перпендикулярна оси Ох (если
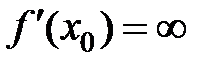
) (см. рис. 10,б, в), либо касательную провести невозможно (если
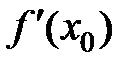
не существует)(см. рис. 10,а).
Определение 21. Критическими точками первого рода называются точки, в которых производная функции 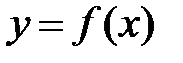 равна нулю либо равна бесконечности, либо не существует.
равна нулю либо равна бесконечности, либо не существует.
Критические точки должны входить в область определения функции.
Теорема 8 (достаточное условие экстремума). Если непрерывная функция 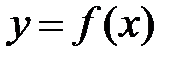 дифференцируема в некоторой
дифференцируема в некоторой 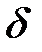 -окрестности критической точки
-окрестности критической точки 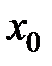 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 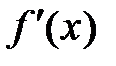 меняет свой знак с плюса на минус, то
меняет свой знак с плюса на минус, то 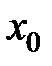 есть точка максимума; с минуса на плюс – точка минимума.
есть точка максимума; с минуса на плюс – точка минимума.
Экстремумы функции находятся среди критических точек первого рода, но критическая точка вовсе не обязательно является точкой экстремума. На рисунке 9,в точка 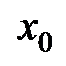 является критической,
является критической, 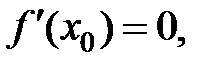 но не является точкой экстремума, так какпри переходе через нее производная
но не является точкой экстремума, так какпри переходе через нее производная 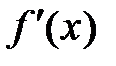 не меняет свой знак.
не меняет свой знак.
В точках экстремума меняется знак производной и вместе с ним меняется характер поведения функции. Таким образом, найдя точки экстремума функции, можно определить интервалы монотонности функции.
2.10.1.Алгоритм исследования функции на монотонность и экстремумы
1) Найти область определения функции 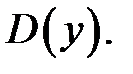
2) Найти производную функции 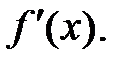
3) Найти критические точки первого рода, решив уравнение 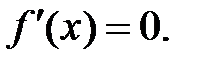
4) На числовую ось нанести область определения функции и критические точки первого рода. В полученных интервалах определить знак производной и поведение функции.
5) Определить, какие из критических точек являются точками экстремума, вычислить значения функции в точках экстремума.
6) Указать интервалы монотонности функции.
Пример 2.8. Найти экстремумы и интервалы монотонности функции:
а) 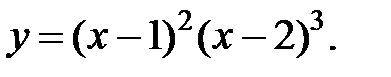
Решение.
1. Найдем область определения функции 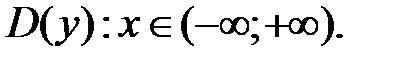
2. Найдем производную функции
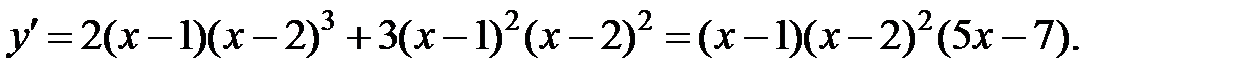
3. Найдем критические точки первого рода, решив уравнение 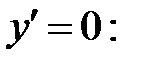
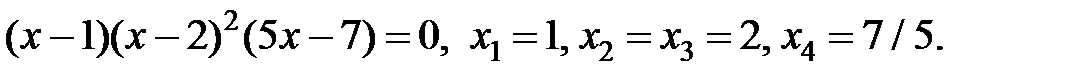 Все корни уравнения принадлежат
Все корни уравнения принадлежат 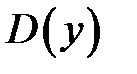 и являются критическими точками первого рода.
и являются критическими точками первого рода.
4. Отметим на числовой оси область определения функции и критические точки первого рода. Строим диаграмму исследования функции на экстремум и интервалы монотонности (рис. 11).
Рис. 11. Интервалы монотонности, точки экстремума
5. Точки экстремума: 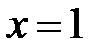 − точка максимума,
− точка максимума, 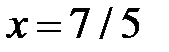 −точка минимума, в точке
−точка минимума, в точке 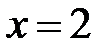 экстремума нет. Вычислим значения функции в точках экстремума:
экстремума нет. Вычислим значения функции в точках экстремума: 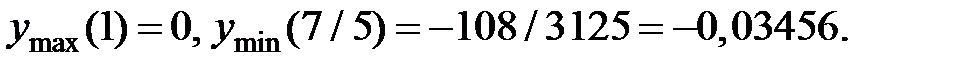 Таким образом,
Таким образом, 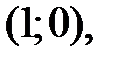
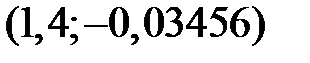 − точки экстремума графика функции.
− точки экстремума графика функции.
6. Интервалы возрастания: 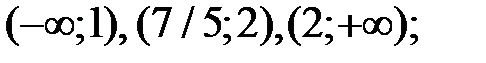 убывания:
убывания: 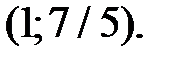
б) 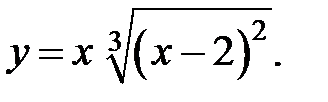
1. 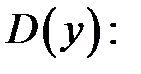
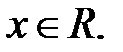
2. 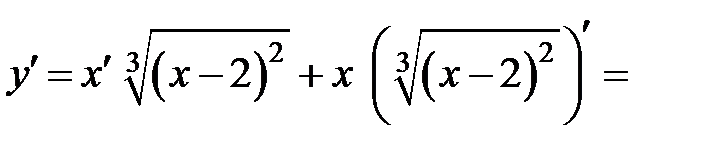
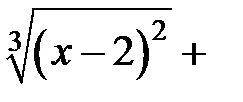
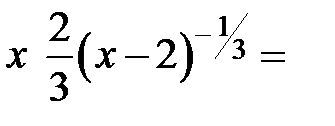
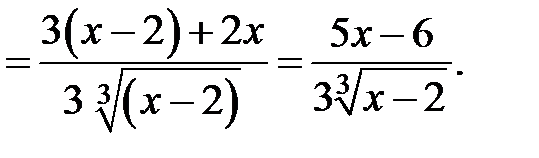
3. 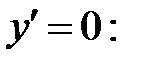
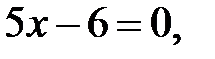
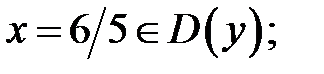
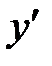 − не существует в точке
− не существует в точке 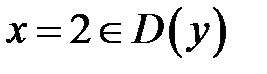
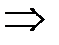
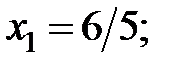
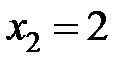 − критические точки первого рода.
− критические точки первого рода.
4. Результаты исследования нанесем на диаграмму (рис. 12).
Рис. 12. Интервалы монотонности, точки экстремума
5. Из диаграммы на рис. 12 видно, что функция имеет максимум в точке
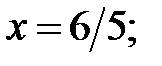 минимум − в точке
минимум − в точке 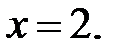
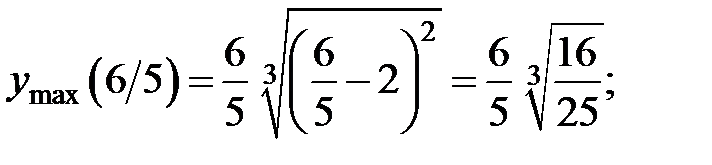
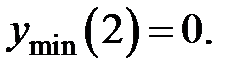 Таким образом,
Таким образом, 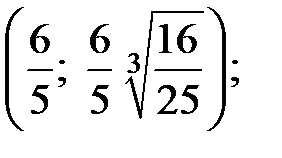
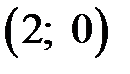 − точки экстремума графика функции.
− точки экстремума графика функции.
6. Интервалы возрастания функции: 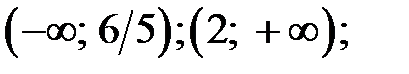 интервал убывания функции:
интервал убывания функции: 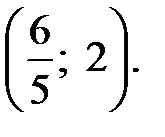
в) 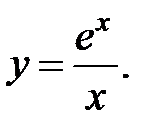
1. 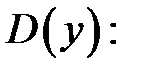
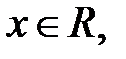
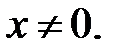
2. 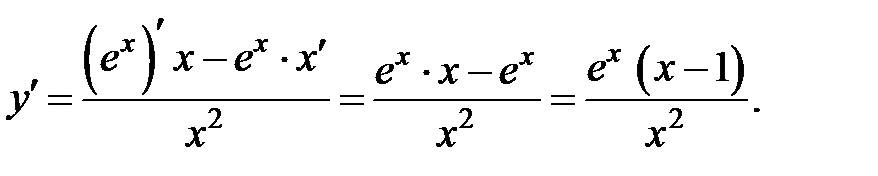
3. 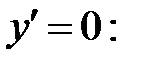
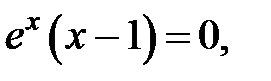
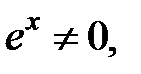
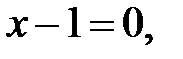
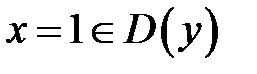 ,
, 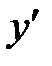 не существует, при
не существует, при 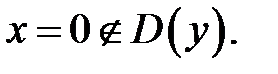 Следовательно,
Следовательно, 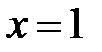 − критическая точка первого рода.
− критическая точка первого рода.
4. Строим диаграмму (рис.13).
Рис. 13. Интервалы монотонности, точки экстремума
5. Из диаграммы на рис. 13 видно, что функция имеет минимум в точке 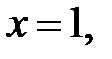
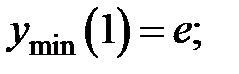
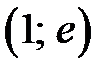 − точка минимума графика функции.
− точка минимума графика функции.
6. Интервалы убывания функции: 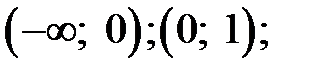 интервал возрастания функции:
интервал возрастания функции: 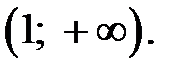
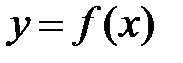 определена на множестве D. Если для любых значений аргументов
определена на множестве D. Если для любых значений аргументов 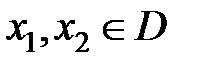 из неравенства
из неравенства 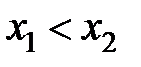 вытекает неравенство
вытекает неравенство 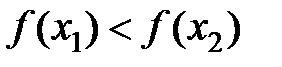 , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве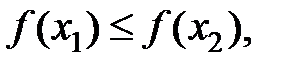 то функция называется неубывающей на множествеD; если
то функция называется неубывающей на множествеD; если 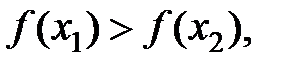 то функция называется убывающей на множествеD; при
то функция называется убывающей на множествеD; при 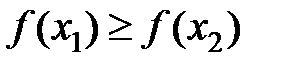 функция называется невозрастающей на множествеD.
функция называется невозрастающей на множествеD. 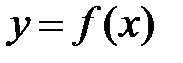 (рис. 7) убывает на интервале (-2;1) (строго монотонна), не убывает на интервале (1;5) (монотонна), возрастает на интервале (3;5) (строго монотонна).
(рис. 7) убывает на интервале (-2;1) (строго монотонна), не убывает на интервале (1;5) (монотонна), возрастает на интервале (3;5) (строго монотонна).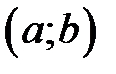 функция
функция 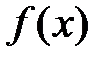 возрастает (убывает), то
возрастает (убывает), то 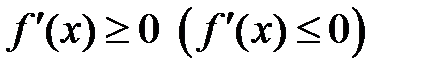 для любых
для любых 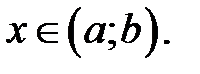
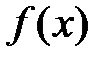 дифференцируема на интервале
дифференцируема на интервале 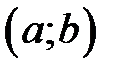 и
и 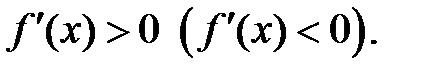 для любых
для любых 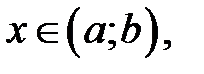 то эта функция возрастает (убывает) на интервале
то эта функция возрастает (убывает) на интервале 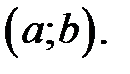
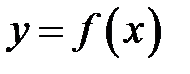 определена в точке
определена в точке 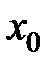 и в некоторой окрестности этой точки.Точка
и в некоторой окрестности этой точки.Точка 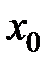 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 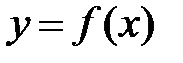 , если существует такая
, если существует такая 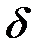 -окрестность точки
-окрестность точки 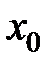 , что для всех
, что для всех 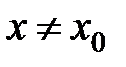 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 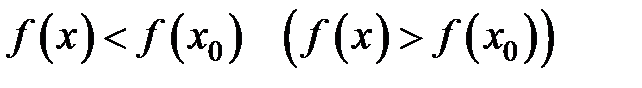 (рис. 9а, б; рис. 10).
(рис. 9а, б; рис. 10).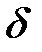 -окрестностью точки
-окрестностью точки 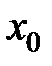 . Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой точке. Наличие максимума (минимума) в отдельной точке данного промежутка вовсе не означает, что в этой точке функция
. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой точке. Наличие максимума (минимума) в отдельной точке данного промежутка вовсе не означает, что в этой точке функция 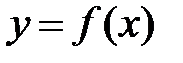 принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)). В данномучебно-методическом пособии мы будем рассматривать только локальные экстремумы.
принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)). В данномучебно-методическом пособии мы будем рассматривать только локальные экстремумы.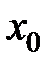
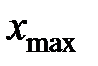
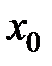 − точка локального экстремума для функции
− точка локального экстремума для функции 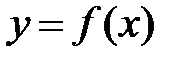 , то в этой точке производная функции либо равна (
, то в этой точке производная функции либо равна ( 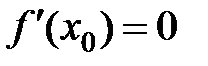 ),либо не существует.
),либо не существует. 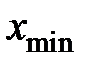
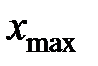
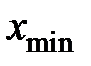
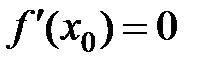 ) (см. рис. 9,а, б), либо перпендикулярна оси Ох (если
) (см. рис. 9,а, б), либо перпендикулярна оси Ох (если 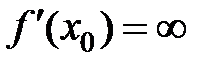 ) (см. рис. 10,б, в), либо касательную провести невозможно (если
) (см. рис. 10,б, в), либо касательную провести невозможно (если 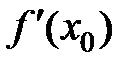 не существует)(см. рис. 10,а).
не существует)(см. рис. 10,а). 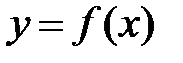 равна нулю либо равна бесконечности, либо не существует.
равна нулю либо равна бесконечности, либо не существует.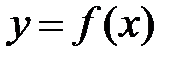 дифференцируема в некоторой
дифференцируема в некоторой 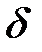 -окрестности критической точки
-окрестности критической точки 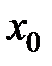 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 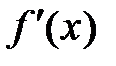 меняет свой знак с плюса на минус, то
меняет свой знак с плюса на минус, то 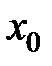 есть точка максимума; с минуса на плюс – точка минимума.
есть точка максимума; с минуса на плюс – точка минимума.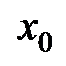 является критической,
является критической, 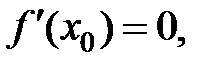 но не является точкой экстремума, так какпри переходе через нее производная
но не является точкой экстремума, так какпри переходе через нее производная 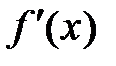 не меняет свой знак.
не меняет свой знак.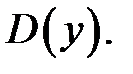
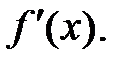
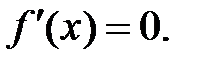
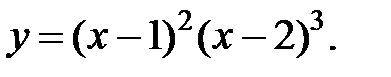
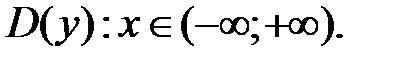
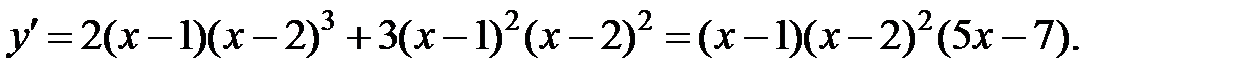
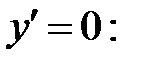
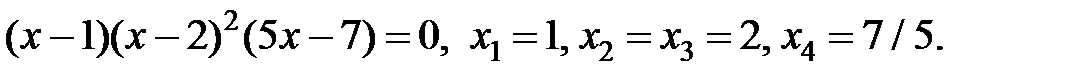 Все корни уравнения принадлежат
Все корни уравнения принадлежат 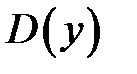 и являются критическими точками первого рода.
и являются критическими точками первого рода.


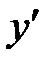
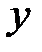
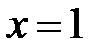 − точка максимума,
− точка максимума, 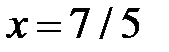 −точка минимума, в точке
−точка минимума, в точке 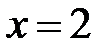 экстремума нет. Вычислим значения функции в точках экстремума:
экстремума нет. Вычислим значения функции в точках экстремума: 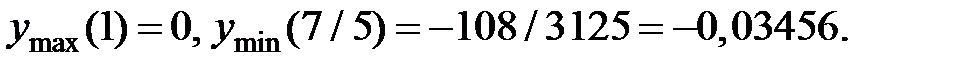 Таким образом,
Таким образом, 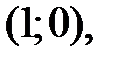
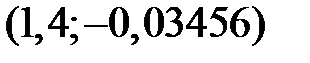 − точки экстремума графика функции.
− точки экстремума графика функции.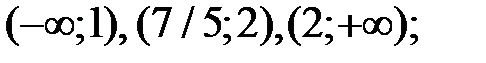 убывания:
убывания: 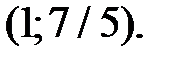
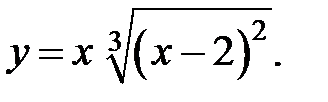
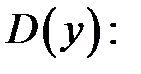
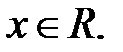
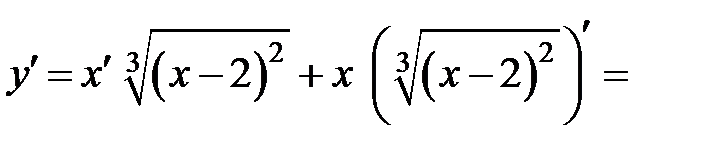
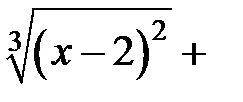
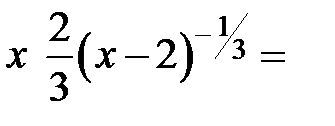
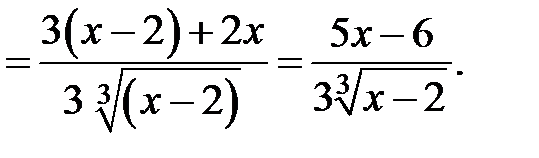
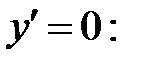
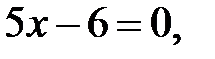
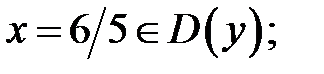
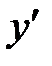 − не существует в точке
− не существует в точке 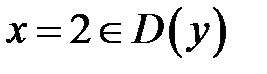
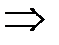
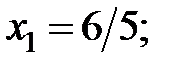
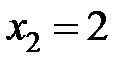 − критические точки первого рода.
− критические точки первого рода.

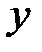
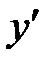
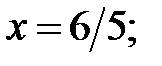 минимум − в точке
минимум − в точке 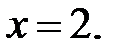
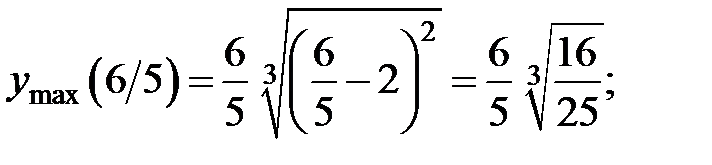
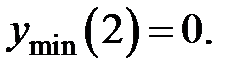 Таким образом,
Таким образом, 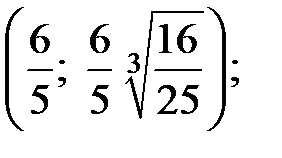
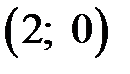 − точки экстремума графика функции.
− точки экстремума графика функции.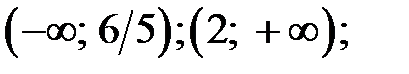 интервал убывания функции:
интервал убывания функции: 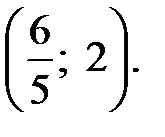
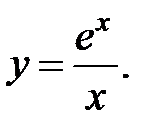
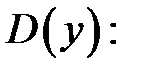
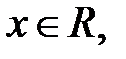
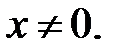
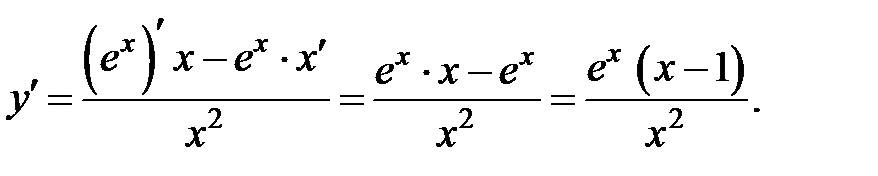
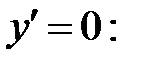
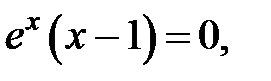
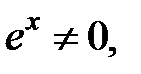
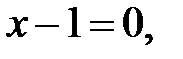
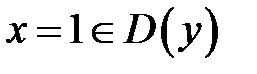 ,
, 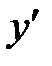 не существует, при
не существует, при 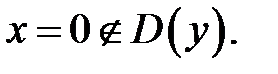 Следовательно,
Следовательно, 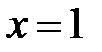 − критическая точка первого рода.
− критическая точка первого рода.

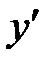
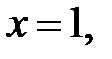
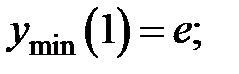
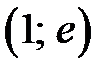 − точка минимума графика функции.
− точка минимума графика функции.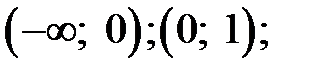 интервал возрастания функции:
интервал возрастания функции: