II. Система трех линейных уравнений с тремя неизвестными

Система трех линейных уравнений с тремя неизвестными имеет вид

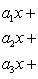
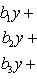
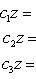
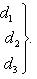(7)

Определитель

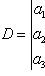
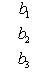
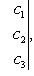(8)

составленный из коэффициентов при неизвестных, называется определителем системы.

1. Если определитель системы 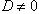, то система (7) имеет решение, и притом единственное. Это решение находится по формулам

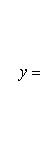
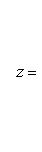
(9)

Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

Определители, стоящие в числителях дробей (9), будем обозначать соответственно через D_x, D_y, D_z.

2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей D_x, D_y и D_z не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если D = 0 и все определители, стоящие в числителях дробей (9), - D_x, D_y, D_z - равны нулю, т. е. если

D = D_x = D_y = D_z = 0,

но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.

4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей D_x, D_y, D_z не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.

5. Если в определителях D, D_x, D_y, D_z все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.

Векторная алгебра

Основные сведения из векторной алгебры. Различают два рода величин: скалярные и векторные.

1. Если некоторая величина вполне определяется ее числовым значением, то ее называют скалярной. Примерами скалярных величин могут служить: масса, плотность, работа, сила тока, температура. Скаляры являются алгебраическими величинами и с ними можно производить любые алгебраические действия: сложение, вычитание, умножение, деление, возведение в степень и т. д.

2. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или вектором. Примерами векторных величин являются скорость, ускорение, сила. Длина вектора называется также его модулем, или абсолютной величиной.

3. Вектор обозначается графически отрезком прямой, на котором ставится стрелка, указывающая направление вектора (см. рисунок).

Будем обозначать вектор одной буквой с черточкой над ней, например, 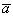, а модуль этого вектора - той же буквой, только без черточки над ней, т. е. a. Модуль вектора a часто обозначается .

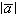Вектор будем также обозначать 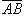, где A - начало и B - конец вектора, а его модуль - теми же буквами, но без черточки наверху.

4. Вектор равен нулю, если его модуль равен нулю. Такой вектор называется нулевым.

5. Два вектора и называются равными, если: 1) равны их модули, 2) они параллельны и 3) направлены в одну и ту же сторону.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными. Вектор, противоположный вектору , обозначается через .

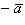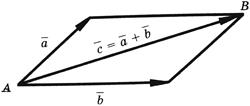
6. Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов и , приведенных к общему началу, есть третий вектор 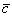, длина которого равна длине параллелограмма, построенного на векторах и , а направлен он от точки A к точке B (см. рисунок):

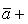
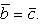
Модуль вектора 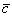вычисляется по формуле

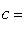
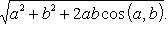(1)

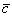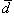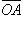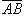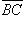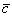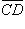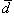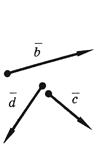
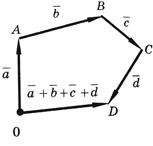
7. Сумму нескольких векторов, например , , и , строят так: берут произвольную точку O плоскости и из нее строят вектор , равный вектору ; из точки A проводят вектор , равный вектору , из точки B - вектор , равный вектору и, наконец, из точки C строят вектор , равный вектору . Вектор 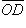, замыкающий полученную ломаную линию OABCD, и будет суммой векторов , , 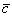и 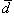(см. рисунок ниже):

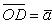
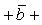
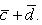
По такому же правилу строится и сумма любого числа векторов.

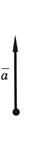
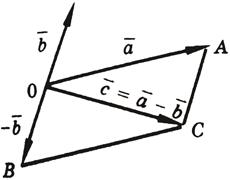
8. Разностью двух векторов и называется такой третий вектор 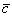, который равен сумме векторов и 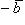(см. рисунок). Вектор 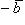параллелен вектору , равен ему по модулю, но противоположно направлен:

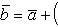
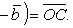
9. При умножении вектора на скаляр k получается вектор , модуль которого равен модулю вектора , умноженному на k, т. е. b = ak. Направления векторов и совпадают, если k > 0, и они противоположны, если k < 0. Имеем

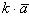
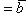, или .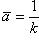

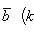
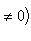10. Два вектора, лежащие на параллельных прямых, независимо от того, направлены они одинаково или противоположно, называются коллинеарными.

11. Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице.

12. Проекцией вектора на ось 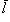называется длина отрезка A'B', заключенного между проекциями конца и начала вектора на эту ось. Этой длине приписывается знак плюс, если направление отрезка A'B' совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси.

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

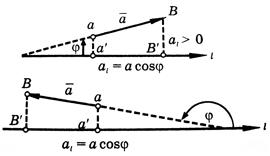
Проекция вектора 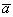на ось 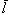обозначается через a_l или 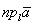, а угол между осью 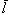и вектором 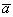будем обозначать так: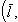 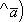. Таким образом,

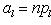
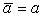
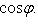(2)

Если 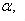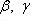- углы, образованные вектором с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора на координатные оси будут равны

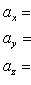
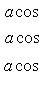
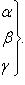(3)

В дальнейшем предполагается, что система координат - прямоугольная.

Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле

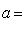
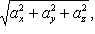(4)

т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.

Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).

Если векторы 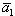и 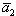равны, то равны и их проекции:

a_1x = a_2x; a_1y = a_2y; a_1z = a_2z. (5)

Если для вектора 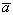известны координаты его начала A(x₁, y₁, z₁) и координаты его конца B(x₂, y₂, z₂), то проекции вектора 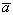на координатные оси определяются по формулам

a_x = x₂ - x₁; a_y = y₂ - y₁; a_z = z₂ - z₁, (6)

а модуль вектора в этом случае определится по формуле

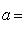
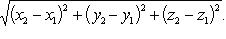(7)

Очевидно, что по формуле (7) следует вычислять и расстояние между точками A(x₁, y₁, z₁) и B(x₂, y₂, z₂).

13. Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось.

Из векторного равенства

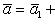
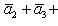
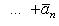(8)

следуют такие три скалярные равенства:

a_x = a_1x + a_2x + a_3x + ... + a_nx;
a_y = a_1y + a_2y + a_3y + ... + a_ny; (9)
a_z = a_1z + a_2z + a_3z + ... + a_nz.

14. Если 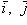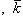- векторы, по модулю равные единице и направленные по координатным осям Ox, Oy и Oz, то разложение вектора по трем координатным осям выражается формулой

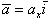
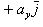
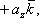(10)

где a_x, a_y и a_z - проекции вектора a на координатные оси - называются координатами вектора (если вектор 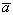имеет координаты a_x, a_y, a_z, то это обозначается так: 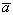{a_x, a_y, a_z}). Если вектор 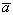имеет начало в начале координат, а его конец A имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

a_x = x; a_y = y; a_z = z.

В этом случае вектор называется радиусом-вектором точки A. Радиус-вектор точки обозначается обыкновенно через 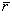(см. рисунок):

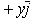
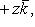(11)

а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле

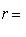
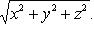(12)

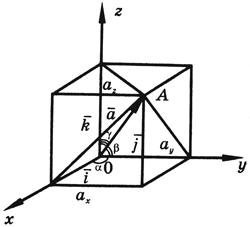
15. Углы, образуемые вектором с координатными осями Ox, Oy и Oz, определяются из формул (3) и (4):

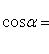
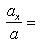
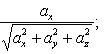
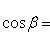
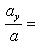
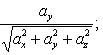(13)

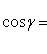
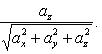
Косинусы, определяемые по этим формулам, называются направляющими косинусами вектора .

Для направляющих косинусов вектора имеет место формула

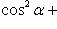
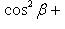
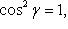(14)

т. е. сумма квадратов косинусов углов, образуемых вектором с тремя взаимно перпендикулярными осями, равна единице.

Если 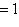, т. е. если - единичный вектор, обозначаемый обыкновенно 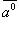, то его проекции на координатные оси вычисляются по формулам

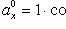
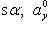
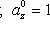
(15)

т. е. проекции единичного вектора 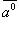на оси прямоугольной системы координат Ox, Oy и Oz равны соответственно направляющим косинусам этого вектора. Имеет место формула

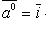
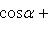
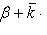
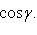(16)

16. Если даны два вектора

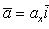
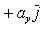
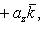
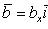
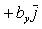
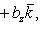
то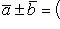

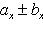
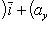
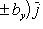
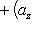
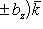
и

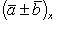
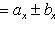
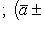
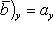
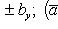
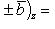
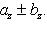(17)

17. Скалярным произведением двух векторов и называется число, равное произведению их модулей на косинус угла между ними. Скалярное произведение векторов и обозначается символом 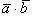. Если обозначить угол между векторами и через 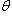, для скалярного произведения будем иметь

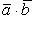
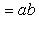
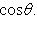(18)

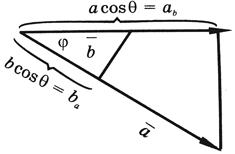
Из формулы (8) следует, что скалярное произведение двух векторов и - это произведение модуля одного из них на проекцию второго на направление первого вектора (см. рисунок):

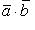
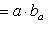
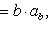(19)

откуда .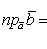

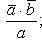
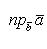
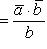Скалярное произведение двух перпендикулярных векторов равно нулю, так как в этом случае .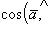

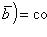
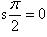Скалярное произведение имеет свойства, аналогичные свойствам произведений чисел:

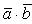
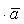
(переместительное свойство умножения);

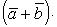
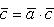
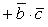
(распределительное, или дистрибутивное свойство произведения).

Если векторы и заданы проекциями на координатные оси

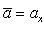
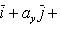
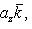
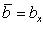
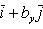
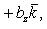
то их скалярное произведение вычисляется по формуле

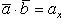
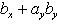
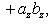(20)

а косинус угла 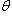между этими векторами определяется по формуле

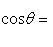
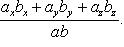(21)

Если углы, образуемые вектором с координатными осями, обозначить через 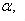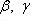, а углы, образуемые вектором с координатными осями, - через 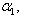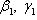, то косинус угла 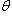между векторами и определяется по формуле

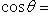
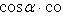
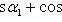
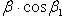
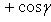
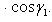(22)

Если векторы и перпендикулярны, то их скалярное произведение равно нулю, и тогда

a_xb_x + a_yb_y + a_zb_z = 0, (23)

или

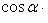
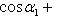
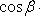
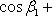
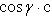
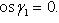(24)

18. Векторным произведением векторов и называется вектор 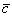, который определяется следующими условиями:

1) Его модуль равен 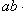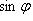где - угол между векторами и .

2) Вектор 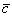перпендикулярен к плоскости, определяемой перемножаемыми векторами и .

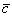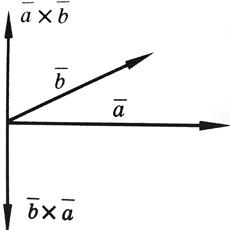
3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

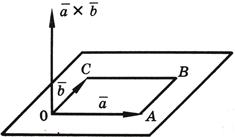
Векторное произведение векторов и обозначается символом :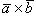

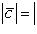
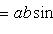
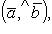(25)

или

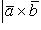
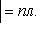
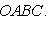(26)

Основные свойства векторного произведения:

1) Векторное произведение 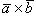равно нулю, если векторы и коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

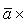
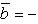
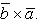
Векторное произведение не обладает свойством переместительности.

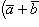
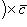
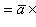
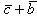
3) 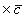(распределительное свойство).

Выражение векторного произведения 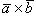через проекции векторов и на координатные оси прямоугольной системы координат дается формулой

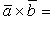
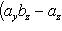
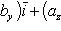
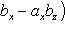
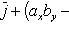
(27)

которую можно записать с помощью определителя

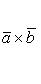
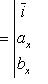
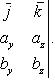(28)

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

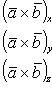
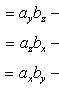
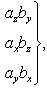(29)

и тогда на основании (4)

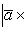
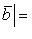
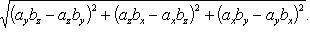(30)

Механический смысл векторного произведения состоит в следующем: если вектор 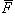- сила, а вектор 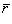есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы 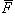относительно точки O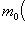 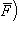есть вектор, равный векторному произведению радиуса-вектора 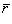точки приложения силы на силу 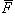, т. е.

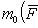
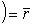
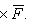
19. Векторно-скалярное произведение трех векторов , и 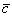или смешанное их произведение вычисляется по формуле

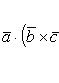
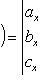
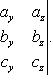(31)

Абсолютная величина векторно-скалярного произведения равна объему параллелепипеда, построенного на векторах , и 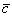. Объем пирамиды, построенной на векторах , и 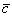, получим по формуле

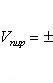
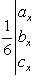
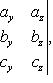(32)

причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы , и 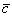не лежат в одной плоскости).

20. Три вектора , и 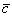называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.