Задача № 7. Расчёт разветвленной электрической цепи однофазного синусоидального тока
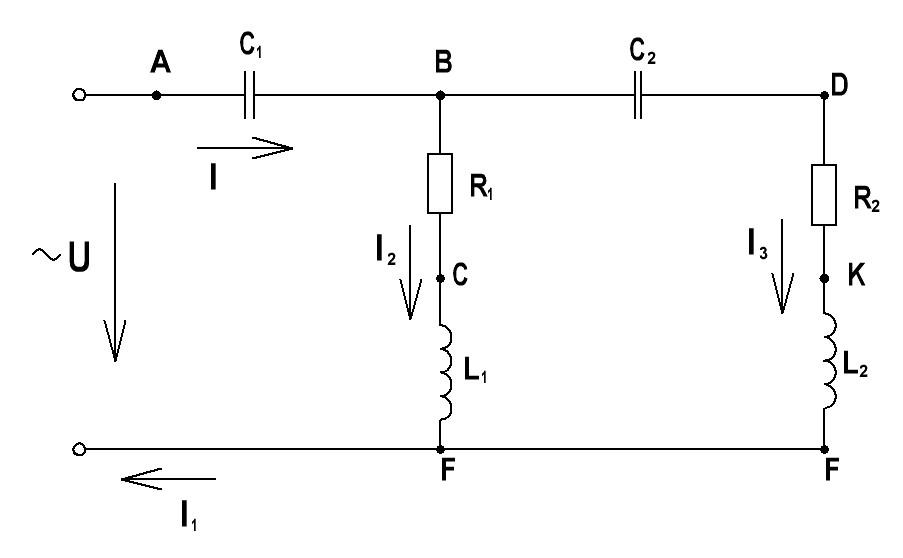
К зажимам электрической цепи подключен источник синусоидального напряжения и(t)=Um sin(ωt + φо) В, частотой f=50 Гц. Амплитуда, начальная фаза напряжения и параметры элементов цепи заданы в таблице. Схема замещения приведена на схеме.
Числовые параметры схем однофазных электрических цепей переменного тока:
| № вари- анта | Um, В | φо, град | R1, Ом | R2, Ом | L1, мГн | L2, мГн | C1, мкФ | C1, мкФ |
| 127,2 | 190,8 | 39,8 | 53,0 |
Выполнить следующее:
1) определить реактивные сопротивления элементов цепи;
2) определить действующее значение токов во всех ветвях цепи;
3) записать уравнение мгновенного значения тока источника;
4) составить баланс активных и реактивных мощностей;
5) построить векторную диаграмму токов, совмещённую с топографической векторной диаграммой напряжений.
Решение:
Находим реактивные сопротивления элементов цепи:
ω = 2πf;
XL1 = ωL1 = 2∙3,14∙50∙0,1272 = 39,941 Ом;
XL2 = ωL2 = 2∙3,14∙50∙0,1908 = 59,911 Ом;
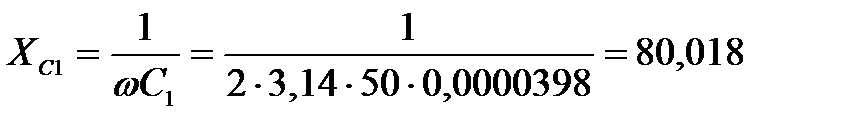 Ом;
Ом;
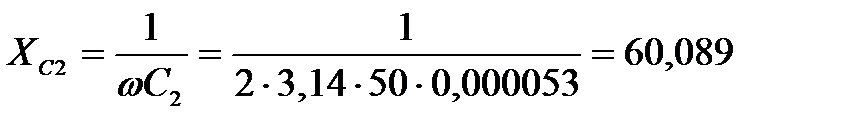 Ом;
Ом;
Расчёт токов в ветвях цепи выполняем методом эквивалентных преобразований. Представим приведённую схему в следующем виде.
Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
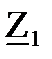 = – j∙XС1 = – j∙80,018 = 80,018∙e –j∙90 Ом;
= – j∙XС1 = – j∙80,018 = 80,018∙e –j∙90 Ом;
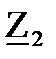 = R1 + j∙XL1 = 40 + j∙39,941 = 56,53∙e j∙44,96 Ом;
= R1 + j∙XL1 = 40 + j∙39,941 = 56,53∙e j∙44,96 Ом;
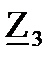 = R2 + j(XL2 – XC2 )= 60 + j∙(59,911 – 60,089) = 60 – j∙0,178 = 60∙e – j∙0,17 Ом;
= R2 + j(XL2 – XC2 )= 60 + j∙(59,911 – 60,089) = 60 – j∙0,178 = 60∙e – j∙0,17 Ом;
Рассчитаем эквивалентное сопротивление цепи, упростив её методом сворачивания:
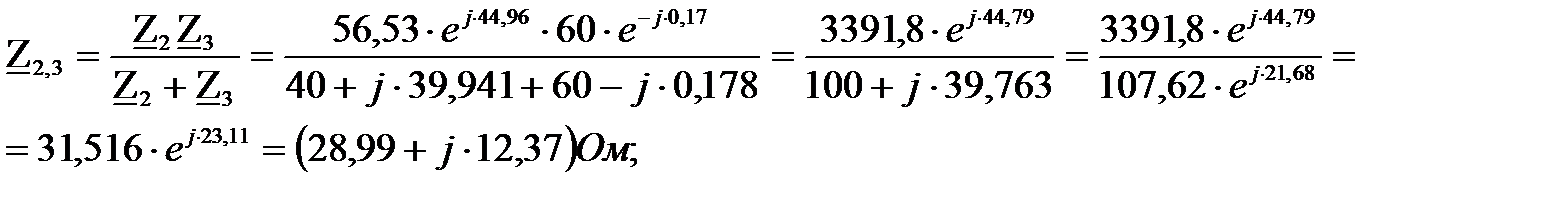
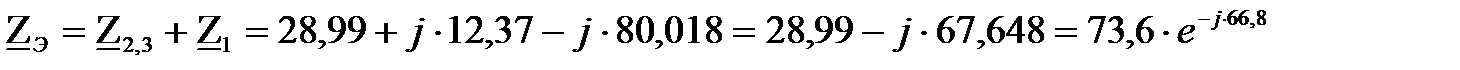 Ом.
Ом.
Выразим действующее значение напряжений в комплексной форме:
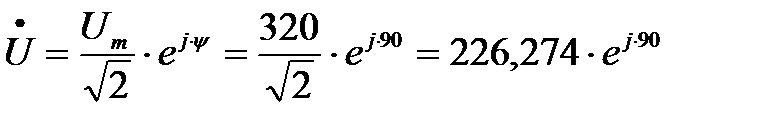 B;
B;
Вычисляем общий ток цепи, после чего определяем каждый ток ветви:
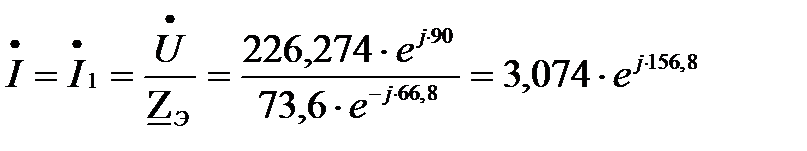 А;
А;
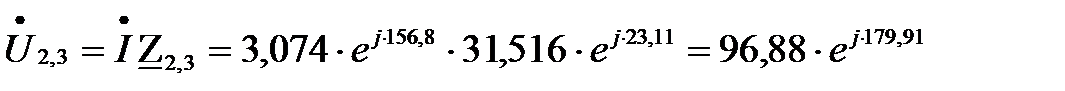 B;
B;
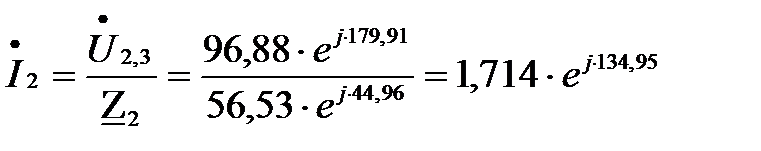 A;
A;
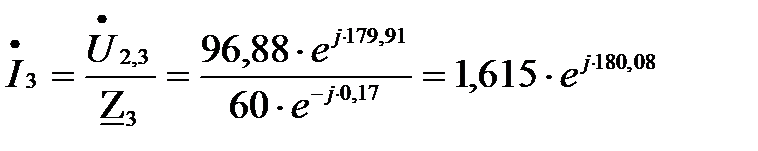 А;
А;
Запишем уравнение мгновенного тока источника:
i = Imsin(ωt+φi), где Im – амплитуда (модуль тока, умноженный на 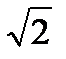 ),
),
φi – начальная фаза (аргумент тока).
i = 3,074∙ 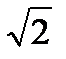 sin(314t + 156,8°) = 4,347∙sin(314t + 156,8°) A;
sin(314t + 156,8°) = 4,347∙sin(314t + 156,8°) A;
Рассчитаем комплексные мощности цепи:
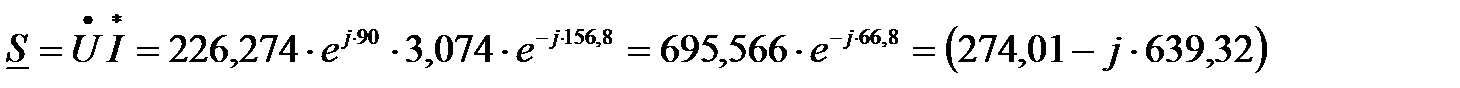 ВА,
ВА,
из чего следует, что Pист = 274,01 Вт; Qист. = –639,32 вар;
Теперь определим активную и реактивную мощности приёмников:
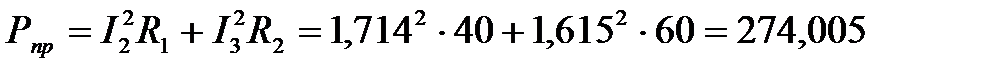 Вт;
Вт;
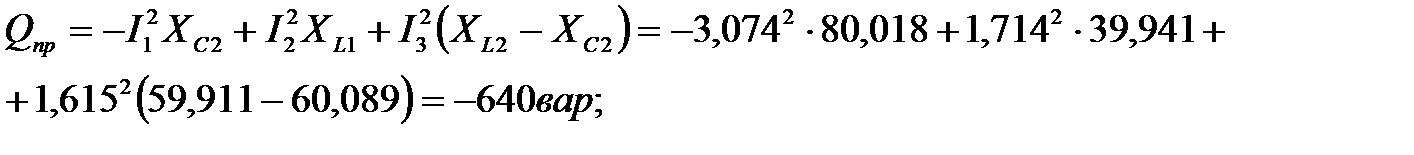 Сравниваем значения:
Сравниваем значения:
274,01 ≈ 274,005 Ри ≈ Рпр
–639,32 ≈ –640 Qи ≈ Qпр
Разница в результате несущественная, а это значит, что баланс сошёлся, так как левая и правая части уравнений должны быть равны. Следовательно, расчёты произведены верно.
Находим напряжения на элементах схемы замещения цепи, а также длину векторов этих напряжений при масштабах 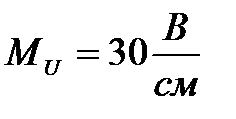 и
и 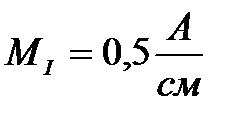 :
:
UAB = I1XC1 =3,074∙80,018=245,975В,
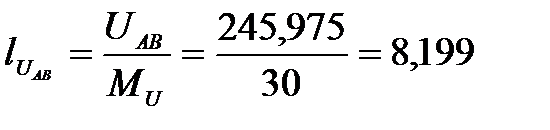 см,
см,
UBC = I2R1 = 1,714∙40 = 68,56 В,
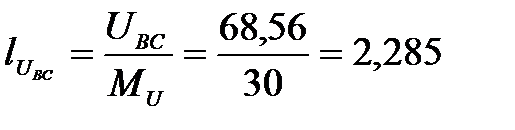 см,
см,
UCF = I2XL1 = 1,714∙39,941=68,459 В,
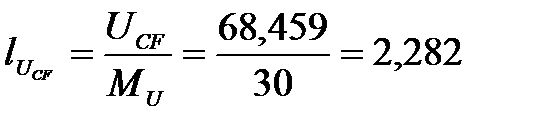 см,
см,
UBD = I3XC2 = 1,615∙60,089=97,044 В,
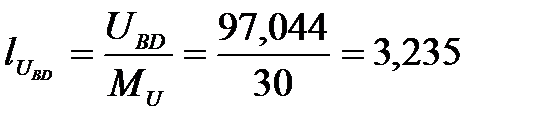 см,
см,
UDK = I3R2 =1,615∙60 = 96,9 В,
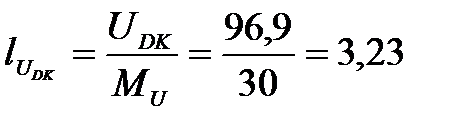 см,
см,
UKF = I3XL2 = 1,615∙59,911 = 96,756 В,
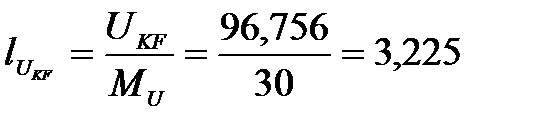 см,
см,
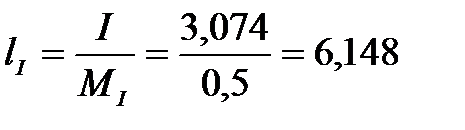 см,
см,
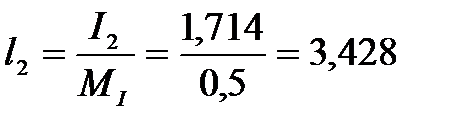 см,
см,
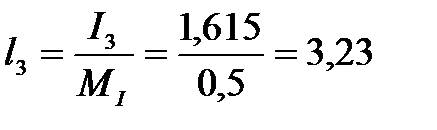 см,
см,
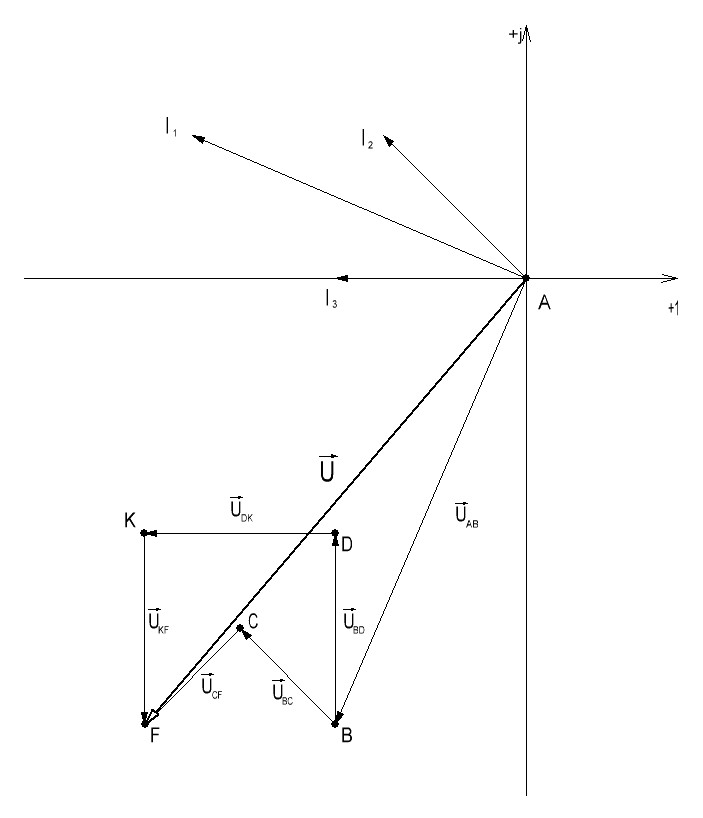
Строим топографическую диаграмму на комплексной плоскости.
На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчётными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелки, а отрицательные – по часовой стрелке. Так, например, вектор тока 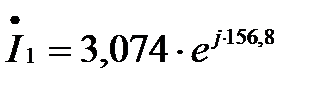 A повёрнут против часовой стрелки относительно оси (+1) на угол 156,8◦ и в длину равен l2.
A повёрнут против часовой стрелки относительно оси (+1) на угол 156,8◦ и в длину равен l2.
Топографическая диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определённая точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока следующим образом:
– на активном сопротивлении ток и напряжение совпадают по фазе;
– на индуктивном элементе напряжение опережает ток на 90°;
– на ёмкости напряжение отстаёт от тока на 90°.
Направление обхода участков цепи выбираем по положительному направлению токов. Обход начинаем от точки А, потенциал которой принимаем за исходный φА = 0. Точку А помещаем в начало координат комплексной плоскости. При переходе от точки А к точке B потенциал изменяется на величину падения напряжения на сопротивлении. Вектор этого напряжения UAB откладываем от точки A под углом –90˚ от вектора тока I. Конец вектора UAB определяет потенциал точки B. Вектор UBC совпадает по фазе c вектором тока I2. От конца вектора UBC откладываем вектор UCF под углом 90˚ от вектора тока I2. Аналогично строим векторы напряжений других участков цепи.
На основании 2-го закона Кирхгофа в векторном виде 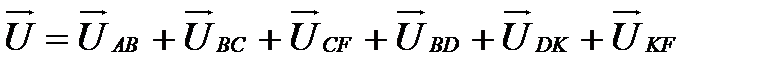 , поэтому, соединив прямой точки F и A, получим вектор напряжения на зажимах цепи. Измерим его длину и по масштабу определим величину напряжения:
, поэтому, соединив прямой точки F и A, получим вектор напряжения на зажимах цепи. Измерим его длину и по масштабу определим величину напряжения:
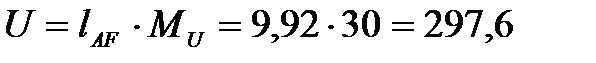 В;
В;
Задача 8. Расчёт трёхфазных линейных электрических цепей переменного тока.
В соответствии с данными начертить схему соединения сопротивлений в трёхфазной цепи.
Определить:
· фазные токи;
· ток в нулевом проводе;
· активную, реактивную и полную мощность каждой фазы и всей трёхфазной цепи;
· угол сдвига фаз между током и напряжением в каждой фазе;
· начертить в масштабе векторную диаграмму трёхфазной цепи.
В цепи, изображённой на схеме, потребители трёхфазного тока соединены звездой.
