Признак сходимости д’Аламбера в предельной форме
Если существует предел
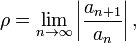
то рассматриваемый ряд абсолютно сходится если 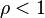 , а если
, а если 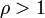 — расходится .
— расходится .
Замечание. Если 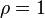 , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
3.4)
. УСЛОВИЕ СХОДИМОСТИ ПОЛОЖИТЕЛЬНОГО РЯДА
Определение 1. Числовой ряд называется положительным, если все его элементы не отрицательны.
Теорема 1. Последовательность частичных сумм положительного ряда монотонно возрастает.
Доказательство. Пусть дан положительный числовой ряд
, где . (А)
Рассматривается n-ная частичная сумма
, тогда
,
это значит, что последовательность частичных сумм монотонно возрастает.
Рассматривается основная в теории положительных рядов теорема.
Теорема 2. Необходимое и достаточное условие сходимости положительного ряда. Для того чтобы положительный ряд сходился, необходимо и достаточно чтобы последовательность частичных сумм была ограничена сверху.
Доказательство. Пусть дан положительный ряд
, где . (А)
1) Необходимость. Пусть ряд (А) сходится, тогда .
Значит, данная последовательность частичных сумм ограничена сверху.
2) Достаточность. Пусть последовательность частичных сумм Sn ограничена сверху, значит, на основании теоремы Вейерштрасса, такая последовательность имеет конечный предел. Отсюда ряд (А) сходится.
Все признаки сходимости (и расходимости), в конечном счете, основаны на этой простой теореме. Но непосредственное ее применение лишь в редких случаях позволяет судить о характере ряда. В качестве примера применения данной теоремы могут служить ряды Дирихле.
2. ОБОБЩЕННЫЕ ГАРМОНИЧЕСКИЕ РЯДЫ ИЛИ РЯДЫ ДИРИХЛЕ
Определение 2. Числовой ряд называется гармоническим рядом, а числовые ряды , где , называются обобщенными гармоническими или рядами Дирихле.
Замечание 1. Название гармонического ряда связано с тем, что каждый его член, начиная со второго, является средним гармоническим для двух соседних. (Число c называется средним гармоническим чисел a и b, если ).
1) Рассматривается гармонический ряд .
Имеет место очевидное неравенство:
. (1)
Если, отбросив первые два члена, остальные члены гармонического ряда разбить на группы по 2, 4, 8,…, 2k-1,… членов в каждой
то каждая из этих сумм в отдельности будет больше ; в этом легко убедиться, полагая в (1) поочередно n = 2, 4, 8, …, 2k-1, … Обозначили n-ную частичную сумму гармонического ряда через Hn; тогда, очевидно,
.
Отсюда следует, что частичные суммы не могут быть ограничены сверху: ряд имеет бесконечную сумму.
2) Рассматривается ряд Дирихле .
Он содержит в себе, как частный случай (при s=1), предыдущий ряд.
Так как при s1; положили для удобства , где .
Аналогично (1), получается неравенство:
. (2)
Выделив, как и выше, последовательные группы членов:
с помощью (2) легко показать, что эти суммы соответственно меньше членов геометрической прогрессии
.
В таком случае ясно, что какую бы частичную сумму рассматриваемого ряда ни взять, она будет меньше постоянного числа
следовательно ряд сходится.
Примеры. Исследовать на сходимость ряды:
1) .
Этот ряд является рядом Дирихле с s>1, а, значит, ряд сходится.
2) .
Этот ряд также является рядом Дирихле с s1, поэтому ряд расходится.
4) .
Это опять же геометрический ряд, его знаменатель равен , а, значит, ряд сходится. Ищется его сумма:
3.5)
| Знакопеременные ряды. Абсолютная и условная сходимость |
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что 1. an+1 < an для всех n; 2. 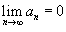 . Тогда знакочередующиеся ряды . Тогда знакочередующиеся ряды 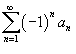 и и 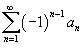 сходятся. Абсолютная и условная сходимость Ряд сходятся. Абсолютная и условная сходимость Ряд 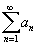 называется абсолютно сходящимся, если ряд называется абсолютно сходящимся, если ряд 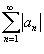 также сходится. Если ряд также сходится. Если ряд 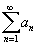 сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно. Ряд 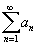 называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. |
3.6)Ряд Тейлора
Определение
Пусть функция 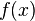 бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки 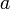 . Формальный ряд
. Формальный ряд
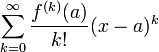
называется рядом Тейлора функции 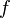 в точке
в точке 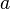 .
.
Связанные определения
- В случае, если
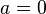 , этот ряд также называется рядом Макло́рена.
, этот ряд также называется рядом Макло́рена.
Свойства
- Если
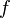 есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке
есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке 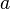 области определения
области определения 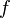 сходится к
сходится к 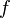 в некоторой окрестности
в некоторой окрестности 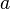 .
. - Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности
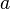 . Например, Коши предложил такой пример:
. Например, Коши предложил такой пример:
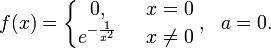
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке 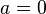 равны нулю.
равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
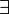 точка точка 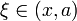 при при 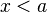 или или 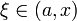 при при 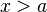 : : 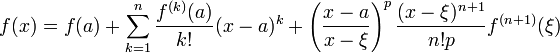 |
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

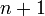 производную в некоторой окрестности точки
производную в некоторой окрестности точки 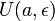
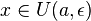
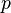 — произвольное положительное число,
— произвольное положительное число,