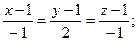Геометрический смысл полного дифференциала

Касательная плоскость и нормаль к поверхности.

нормаль

N

j N₀

касательная плоскость

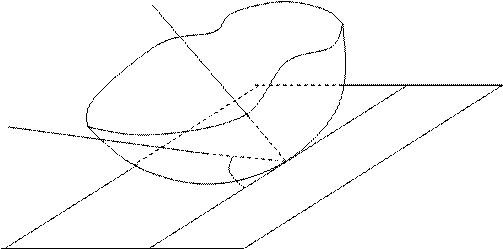
Пусть N и N₀ – точки данной поверхности. Проведем прямую NN₀. Плоскость, которая проходит через точку N₀, называется касательной плоскостью к поверхности, если угол между секущей NN₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN₀.

Определение. Нормальюк поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), касательная плоскость в точке N₀(x₀,y_0,(x₀,y₀)) существует и имеет уравнение:

.

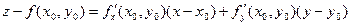Уравнение нормали к поверхности в этой точке:

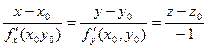
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х₀, у₀) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х₀, у₀) к точке (х₀+Dх, у₀+Dу).

Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.

Пример. Найти уравнения касательной плоскости и нормали к поверхности

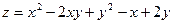
в точке М(1, 1, 1).

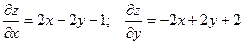
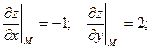
Уравнение касательной плоскости:

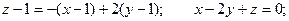
Уравнение нормали: