Показатели частной корреляции

Ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено через 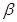- коэффициенты, а так же с помощью частных коэффициентов корреляции (только для линейных связей). Частные показатели корреляции широко используются при отборе факторов модели: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

Для уравнения множественной регрессии

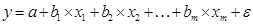
Коэффициент частной корреляции, измеряющей влияние нау фактора 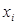, при неизменном уровне других факторов, можно определить по формуле

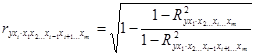, где

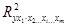- множественный коэффициент детерминации всего комплекса m факторов с результатом;

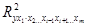- множественный коэффициент детерминации, но без введения в модель фактора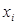

Пример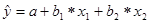

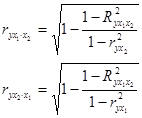
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Коэффициенты парной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле

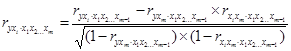
Запишем формулу для двухфакторной модели

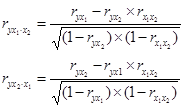
Частные коэффициенты корреляции, рассчитанные по данной рекуррентной формуле для линейной зависимости, изменяются [-1;1]. А коэффициенты корреляции, рассчитанные по формуле через множественные коэффициенты детерминации, изменяются [0;1]. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом.

В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют на этапе формирования модели, в частности в процедуре отсева факторов. Так, при построении многофакторной модели, например, методом исключения переменных на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по t-критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строят новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели существенно не отличаются друг от друга, т.е. 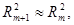где m – число факторов.