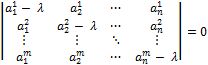Формула вычисления смешанного произведения векторов по их известным декартовым координатам
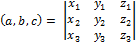 ,
,
где 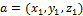 ,
, 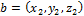 ,
, 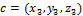 .
.
112. Понятие функции f: х Í Rn→y Í Rm.
Функция – закон или правило, согласно которому каждому элементу 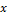 из множества
из множества 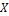 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 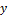 из множества
из множества 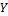 .
.
113. Определение линейного оператора А: Rn→Rm.
Отображение 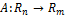 называется линейным оператором, если для любых векторов
называется линейным оператором, если для любых векторов 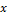 и
и 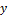 из
из 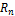 и любых действительных чисел
и любых действительных чисел 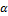 и
и 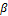 выполняется условие:
выполняется условие:
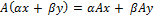
114. Как строится матрица линейного оператора А: Rn→Rm?
В пространстве 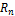 выберем базис
выберем базис 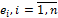 , а в
, а в 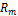 – базис
– базис 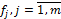 . Подействуем оператором A на каждый базисный вектор
. Подействуем оператором A на каждый базисный вектор 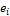 из
из 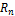 . В результате получим
. В результате получим 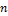 векторов
векторов 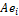 в пространстве
в пространстве 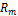 . Разложим их по базису
. Разложим их по базису 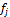 . Получим
. Получим
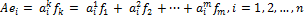 .
.
Из чисел 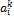 образуем матрицу, записав в её столбцы координаты векторов
образуем матрицу, записав в её столбцы координаты векторов 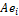 :
:
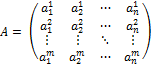
Это и есть матрица линейного оператора.
115. Как найти координаты вектора А[ 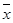 ], зная матрицу оператора А: Rn→Rm?
], зная матрицу оператора А: Rn→Rm?
Для этого нужно матрицу умножить на вектор.
116. Запишите матрицу линейного оператора А: R1→R1.
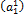
117. Запишите матрицу линейного оператора А: Rn→R1.
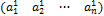
118. Запишите матрицу линейного оператора А: R1→Rn.
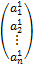
119. Определите операцию сложения двух линейных операторов. Как найти матрицу суммы двух операторов?
Для этого нужно сложить матрицы этих операторов.
Определите операцию умножения оператора на число.
Для этого нужно умножить матрицу этого оператора на данное число.
121. Определите композицию двух линейных операторов. Как найти матрицу композиции линейных операторов А и В?
Для этого нужно перемножить матрицы этих операторов.
Понятие обратного линейного оператора.
Если линейный оператор 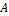 с невырожденной матрицей действует из
с невырожденной матрицей действует из 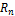 в
в 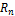 , то для него можно определить обратный оператор
, то для него можно определить обратный оператор 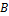 условием
условием 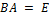 , где
, где 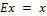 для всех
для всех 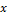 . Матрицы взаимно обратных операторов взаимно обратны, т.е. их произведение даёт единичную матрицу.
. Матрицы взаимно обратных операторов взаимно обратны, т.е. их произведение даёт единичную матрицу.
123. Запишите закон изменения матрицы линейного оператора А: Rn→ Rn при переходе к новому базису.
Пусть матрица оператора в базисе 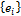 будет равна
будет равна 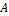 , а в базисе
, а в базисе 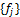 –
– 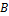 ; матрица
; матрица 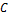 – матрица перехода от одного базиса к другому. Тогда будет верным соотношение:
– матрица перехода от одного базиса к другому. Тогда будет верным соотношение:
 или
или 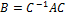
При этом определитель матрицы останется неизменным, что означает следующее: если матрица линейного оператора невырождена в одном базисе, то она невырождена и во всех остальных.
124. Дать определение собственных чисел и собственного вектора линейного оператора
А: Rn→Rn.
Собственный вектор линейного оператора – такой ненулевой вектор 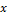 , что
, что 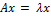 , при этом число
, при этом число 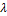 называется собственным числом, отвечающим собственному вектору
называется собственным числом, отвечающим собственному вектору 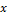 .
.
Запишите характеристическое уравнение матрицы А.
Характеристическое уравнение:
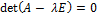
и в матричном виде: