Састық және гомотетия әдістері

АЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ

ЖАРАТЫЛЫСТАНУ ЖӘНЕ МАТЕМАТИКА ЖОҒАРҒЫ МЕКТЕБІ

«ФИЗИКА-МАТЕМАТИКА» КАФЕДРАСЫ

«Геометрияда ұқсас түрлендіру әдісін қолданып есептер шығару»

Д И П Л О М Д Ы Қ Ж Ұ М Ы С

Мамандық -5В010900-Математика

Орындады Берікқызы Н.

Ғылыми жетекшісі Құрмыш Е.

Шымкент 2016

МАЗМҰНЫ

КІРІСПЕ 3

1. Ұқсас түрлендірудің теориялық негізі 5

1.1Ұқсастық және гомотетия әдістері 5

1.2Ұқсас түрлендіру. Ұқсас фигуралар 7

2. Мектеп геометрия курсындағы ұқсас түрлендіру 10

2.1 Ұқсас түрлендіру және оның қасиеттері 10

2.2 Фигуралардың ұқсастығы 12

2.3 Үшбұрыштардың екі бұрышы бойынша ұқсастық белгісі 12

2.4 Үшбұрыштардың екі қабырғасы және олардың арасындағы бұрышы

бойынша ұқсастық белгісі 14

2.5 Үшбұрыштардың үш қабырғасы бойынша ұқсастық белгісі 15

2.6 Тік бұрышты үшбұрыштардың ұқсастығы 16

2.7 Шеңберге іштей сызылған бұрыштар 17

2.8 Шеңбер хордалары кесінділерінің және қиюшылардың

пропорционалдығы 19

3. Геометрияда ұқсас түрлендіру әдісін қолданып есептер шығару 21

3.1 Мектеп геометрия курсындағы салу есептеріндегі ұқсас

түрлендірулерге мысалдар 21

3.2 Планиметрия курсында геометриялық есепті шешудің жалпы әдіс -

тәсілдері және есептерді шешуге мысалдар 30

3.2.1Түрлендіру әдісін қолдануғамысалдар 33

3.2.2 Салуға берілген есептерді ұқсас түрлендіру (гомотетия) әдісімен

шығару мысалдары36

3.3 Кеңістіктегі салу есептерін шешу әдістері жәнесалуға берілген

есептерді шешуге мысалдар 55

ҚОРЫТЫНДЫ 67

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 69

Қосымша А 74

Қосымша В

Қосымша С 78

КІРІСПЕ

Тақырыптың өзектілігі. Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік - дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әр түрлі теориялық фактілерді байланыстыруды қажет ететін, оқушылар шығара алмайтын жаңа есептер де жиі кездеседі. Сондықтан оқушыларды кез келген геометриялық есепті шешудің жалпы тәсілдерімен қаруландыру керек.

Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажет ететін сөйлемдерді дәлелдейміз. Ал есептерді алгебралық әдіспен шешкенде ізделген шаманы табу, не тұжырымдауға тиісті сөйлемді дәлелдеу тікелей есептеу жолымен немесе теңдеулер мен олардың жүйелерін құру арқылы іске асады. Тікелей есептеу әдісінің мәні мынада: есептің берілгендері мен белгісіздерінің жан-жақты байланыстарынан аралық қосымша белгісіз шамалар тізбегі құрылады, тізбекке қатысатын әрбір белгісіз шама анықталады немесе іздеген шама белгілі шамалар арқылы өрнектеледі.

Мектеп геометрия курсын оқытудың негізгі мақсаты - оқушылардың геометрия ғылымының негіздерін меңгеруі мен оларды практикаға қолдануға үйрету, кеңістік түсінігін және елестетуін қалыптастыру, логикалық ойлауын дамыту, негізделген, тұжырымды ой қорытуы мен дәлелдеу қабілетін жетілдіру, ойды дәл және анық жеткізе алу. Осы мақсаттарға жету есептер шығару іс – әрекетін меңгерумен бірге жүзеге асады. Есептер шығару нәтижесінде оқушылар алған білімдерін тиянақтап, теориялық материалды қолдана білуге үйренеді, есеп шығара отырып жаңа білімдер алады. Сонымен қатар, есептер шығару – оқушылардың талдау, жинақтау, салыстыру, жалпылау, нақтылау т.б. ойлау операциясын меңгеретін де ортасы.

Жоғарыда айтылғандар осы зерттеу жұмысы үшін тақырыпты таңдаудың өзектілігін көрсетеді.

Зерттеу нысаны - мектеп геометрия курсында ұқсас түрлендіру әдісіне есептер шығару барысы.

Зерттеу пәні – мектепте геометрияны оқыту әдістемесі.

Жұмыстың негізгі мақсаты – ұқсас түрлендіру әдісіне есептер шығару жолдарын айқындау және есептер шығаруда назар аудару керек болатын жалпы әдістемелік ережелерді жасау.

Болжам: ұқсас түрлендіру әдісіне есептер шығаруды үйрету жоғары дәрежеде болады, егер:

1) ұқсас түрлендіру әдісіне есептер шығаруды үйретуден бұрын қарапайым салу есептерімен жеткілікті жұмыс жүргізілетін болса;

2) Салу есептері тек қана өзіндік нысан ретінде ғана емес, сондай-ақ декарттық координат жүйесінің элементі ретінде де қарастырылады;

3) ұқсас түрлендіру әдісіне есептер шығару, салу есептерін жақсы меңгергеннен соң орындалады;

Зерттеудің міндеттері:Зерттеудің проблемасын шешу, болжамның дұрыстығына көз жеткізу және мақсатқа жету үшін келесі мәселелер орындалады:

- осы тақырып бойынша ғылыми-әдістемелік әдебиеттерді зерттеу;

- заманауи оқу құралдарына осы тақырыптың баяндалуына логикалық дидактикалық талдау жүргізу;

- алынған мәліметтерді жалпылау және жүйелеу;

- жасалынған әдістемені пайдаланудың тиімділігін есептер шығаруда тексеру;

Зерттеу әдістері:Жұмыстың мақсатына жету, болжамды тексеру және жоғарыда қойылған мәселелерді шешу үшін келесі әдістер пайдаланылды:

- мектепте геометрияны оқытуға қатысты бағдарламаларды, оқу құралдарын, әдістемелік материалдарды үйрену;

- әртүрлі авторлық мектеп оқулықтарын салыстырмалы талдау арқылы жұмыс тақырыбына сай материалдарды жинақтау, сұрыптау;

- озат мұғалімдердің іс-тәжірибелерімен танысу, зерделеу;

- сабақ үстінде оқушылардың іс-әрекеттерін бақылау.

Жұмыстың құрылымы:кіріспеден, үш бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен, А,В,С қосымшаларынан құралған.

Бұл жұмыстың материалдары практикалық маңызға ие және 9 сыныптағы мектеп геометрия курсында «Жазықтықтағы түрлендірулер» тақырыбын баяндауда оқытушылардың және студенттердің пайдалануы мүмкін.

Бірінші «Ұқсас түрлендірудің теориялық негізі» бөлімінде ұқсастық және гомотетия әдістеріне, Ұқсас түрлендіру. Ұқсас фигураларға жалпы сипаттама қарастырылған.

Екінші бөлімде «Мектеп геометрия курсындағы ұқсас түрлендіру» тақырыбы материалдарын қысқаша баяндадық және әрбір тақырыпқа есептерді шығарып көрсеттік.

Үшінші «Геометрияда ұқсас түрлендіру әдісін қолданып есептер шығару» бөлімінде мектеп оқушылары жиі кездесетін жазықтықтағы салу есептерін ұқсас түрлендіру (гомотетия) әдісімен шығаруға мысалдар берілді, сондай-ақ кеңістіктегі салу (елестету арқылы орындалатын) есептерін шығаруға аздаған мысалдар берілді.

Қорытындыда салу есептерін орындау бойынша әдістемелік нұсқау берілді.

Қосымша А- Сабақ жоспары (үлгі ретінде) берілген.

Қосымша В- Өзіндік жұмыс үшін планиметриядағы ұқсас түрлендіруге берілетін есептердің үлгілеріберілген.

Қосымша С- Өзіндік жұмыс үшін стереометриядағы салуға берілетін есептердің үлгілері берілген.

1. Ұқсас түрлендірудің теориялық негізі

Шамалардың біртектілігін сараптау және теңдеулерді сараптау әдістерінің айырмашылығы – олардың физикалық қасиеттері мен құбылыстарын жете білуде болып табылады. Бірінші жағдайда шамалар біртектілігіне талдау жасау физикалық шамалардың біртектілігі формулаларына да қолданылады, екінші жағдайда – шамалар арасындағы аналитикалық байланысқа қолданылады.

Бұл бөлімде геометриялық модельдер мен натуралардың физикалық теңдеулер арөылы алыну мысалдары көрсетілген.Бұл жоба бойынша теңдеулерге талдама жасау әдісі біртекті шамаларды талдау әдісімен жақындастырылып, ұқсастықтың классикалық теориясымен сай келеді. Фигуралардың ұқсастығы жайлы ғылым б.э.дейін Ү-ІҮ ғ.ғ. Гиппократ Хиосскийдің, Архит Таренскийдің,Евдокс Книдский т.б. еңбектерінде жарық көрген. Ол Евклидтің ҮІ «Бастау» кітабында да баяндалды. Қасиеттері.Ұқсастық евклид кеңістігінің өзіне бейнеленуі.

Ұқсастық түзу бойындағы нүктелер ретін мақтайды, яғни егер нүкте нүктелер арасында жатса , және , , — олардың сай келетін бейнелері де сол нүктелер арасында жатады . және .

Бір нүктеде жатпайтын нүктелер, кез келген ұқсастықта бір түзу бойында жатпайтын нүктелерге ауысады.

Ұқсастық түзуді түзуге, кесіндіні кесіндіге, сәулені сәулеге, бұрышты бұрышқа, бұрышты бұрышқа, шеңберді шеңберге айналдырады.

Ұқсастық кезінде бұрыш өз шамасын сақтайды.

Ұқсастық өзіндік (өзіндік емес) деп аталынады, егер қозғалыс өзіндік (өзіндік емес) болса. Өзіндік ұқсастық фигуралар ориентациясын сақтайды, ал өзіндік емес – оны қарама-қарсыға өзгертеді.

Екі үшбұрыш бір- біріне ұқсас болып келеді, егер

· Олардың бұрыштары тең болса немесе

жақтары пропорционал болса.

· Ұқсас фигуралар ауданы оларға ұқсас сызықтар квадратына пропорционал (мысалы,жақтарының). Шеңбер аудандары олардың квадраттарының диаметрлеріне қатысты пропорционал (немесе радиустарына).

· Белгілеу

Ұқсастықтарды белгілеу үшін ~белгісі қолданылады.

састық және гомотетия әдістері

Жазықтықтағы L түзуінің бойынан О және А нүктелерін аламыз. Осы түзудің бойында жатқан үшінші нүкте, алғашқы екі нүктеге қатысты қалай анықталатынын көрсетелік.

Анықтама. ОА₁ = кОА шарты орындалатын А нүктесінің бейнесі А₁ болатындай жазықтықты өзіне - өзін бейнелеуді О центрлі коэффициенті к 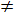О гомотетия деп атайды және оны 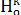(X) 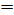Х₁ деп жазады. Мұндағы 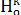— центрі О, коэффициенті к болатын гомотетия. Белгілі бір жазықтықтан Ф фигурасы, О нүктесі, к 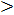О саны берілсін. Ф фигурасының кез келген А нүктесі үшін центрі О, коэффициенті гомотетия арқылы А нүктесінің бейнесі 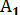нүктесін табуға болады. Осы айтылған гомотетияны қолданғанда Ф фигурасының әрбір нүктесіне гомотетиялы барлық нүктелердің жиыны жаңа бір 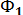фигурасы болады. Сонымен, 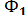фигурасы центрі О және коэффициенті к гомотетияны қолданғанда Ф фигурасының бейнесі болады [32].

Гомотетия коэффициенті к 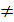0 санының әр түрлі мәндеріне қарай фигураға гомотетиялы фигура түрліше бейнеленеді.

1) К >0 болса, гомотетиялы фигуралар О центрінің бір жағында жатады.

а) 0< к < 1 болса, фигураға гомотетиялы фигура О центрімен әуелгі фигураның арасына бейнеленеді,

б) к > 1 болса, онда берілген фигураға гомотетиялы фигура бастапқы фигураның оң жағына бейнеленеді,

в) к = 1 болса, фигура теңбе-тең бейнеленеді.

2) к < 0 болса, онда гомотетиялы фигуралар О центрінің екі жағына орналасады.

а) к = - 1 гомотетия центрі О нүктесіне қарағандағы симметрия болады.

б) коэффициенті -1< к <0 болатын гомотетия әуелгі фигурадан өлшемдері жөнінен «кішірейітіліп бейнеленеді.

в) к < -1 болса, фигураға гомотетиялы фигура «үлкейіп» бейнеленеді (1-а, б, в, г - суреттер)

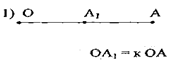
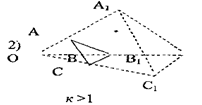
Сурет-1а Сурет-1 б

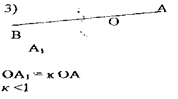
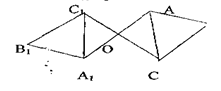
Сурет-1в Сурет-1г