Электростатика и постоянный ток 4 страница

Приняв во внимание, что Q=σS, U₁= Е₁d₁= 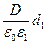и U₂=E₂d₂= 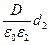, равенство (1) можно переписать в виде

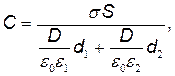(2)

где σ - поверхностная плотность заряда на пластинах; Е₁ и Е₂ - напряженности поля в первом и втором слоях диэлектрика соответственно; D - электрическое смещение поля в диэлектриках.

Умножив числитель и знаменатель равенства (2) на ε₀ и учтя, что D=σ,окончательно получим

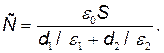
Сделав вычисления по последней формуле (диэлектрические проницаемости фарфора – 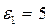; эбонита – 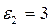), найдем

.

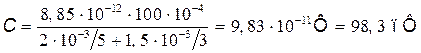Пример 21. Два плоских конденсатора одинаковой электроемкости С₁=С₂=С соединены в батарею последовательно и подключены источнику тока с электродвижущей силой E. Как изменится разность потенциалов U₁ на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью 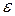=7?

Решение. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова: U₁=U₂= E / 2. После заполнения электроемкость второго конденсатора возросла в ε раз:

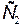=εC₂=εC.

Электроемкость С первого не изменилась, т. е. 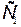=C.

Так как источник тока не отключался, то общая разность потенциалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденсаторе

U₁'=Q/C₁'=Q/C, (1)

где Q - заряд на пластинах конденсатора. Поскольку при последовательном соединении конденсаторов заряд на каждой пластине и на всей батареи одинаков, то

Q = С'_бат E

где 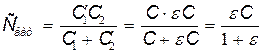- емкость батареи. Таким образом,

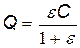E.

Подставив это выражение заряда в формулу (1), найдем

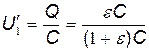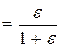E E .

Чтобы найти, как изменилась разность потенциалов на пластинах первого конденсатора, вычислим отношение:

U'₁/U₁=2ε/(1+ε).

После подстановки значения ε получим

U'₁/U₁=1,75.

Следовательно, разность потенциалов на пластинах первого конденсатора после заполнения второго конденсатора диэлектриком возросла в 1,75 раза.

Пример 22.Конденсатор электроемкостью C₁=З мкФ былзаряжен до разности потенциалов U₁=40В. После отключения oт источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором электроемкостью С₂=5мкФ. Определить энергию ΔW,израсходованную на образование искры в момент присоединения второго конденсатора.

Решение. Энергия, израсходованная на выбрасывание искры, равна

ΔW=W₁ – W₂ (1)

где W₁- энергия, которой обладал первый конденсатор до, присоединения к нему второго конденсатора; W₂ - энергия, которую имеет батарея, составленная из первого и второго конденсаторов. Подставив в равенство (1) формулу энергии заряженного конденсатора W=CU²/2и приняв во внимание, что общая электроемкость параллельно соединенных конденсаторов равна сумме электроемкостей отдельных конденсаторов, получим

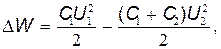(2)

где С₁ и С₂ - электроемкости первого и второго конденсаторов; U₁- разность потенциалов, до которой был заряжен первый конденсатор; U₂ - разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U₂следующим образом: 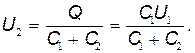Подставив это выражение U₂в формулу (2), получим

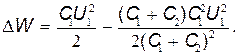
После простых преобразований найдем

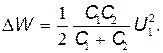
Выполнив вычисления, получим ΔW=1,5мДж.

Пример 23. Плоский воздушный конденсатор с площадью S пластины, равной 500 см², подключен к источнику тока, ЭДС которого равна 300 В. Определить работу А внешних сил по раздвижению пластин от расстояния d₁= 1 см до d₂=3см в двух случаях: 1) пластины перед раздвижением отключаются от источника тока; 2) пластины в процессе раздвижения остаются подключенными к нему.

Решение. 1-й случай. Систему двух заряженных и отклюенных от источника тока пластин можно рассматривать как изолированную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы:

A=ΔW=W₂ – W₁,(1)

где W₂ - энергия поля конденсатора в конечном состоянии (пластины находятся на расстоянии d₂); W₁- энергия поля в начальном состоянии (пластины находятся на расстоянии d₁).

Энергию в данном случае удобно выразить через заряд Q на пластинах, так как заряд пластин, отключенных от источника при их раздвижении, не изменяется. Подставив в равенство (1) выражения

W₂=Q²/ (2С₂) и W₁ =Q²/(2С₁),

получим

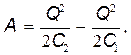или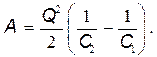

Выразив в этой формуле заряд через ЭДС E источника тока и начальную электроемкость С₁ (Q=C₁ E), найдем

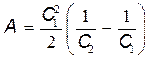E² . (2)

Подставляя в формулу (2) выражения электроемкостей (C₁=ε₀S/d₁и C₂=ε₀S/d₂)плоского конденсатора, получим

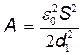E²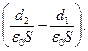

После сокращения на ε₀S формула примет вид

A=ε₀S E²(d₂ – d₁)/2d₁² . (3)

Произведя вычисления по формуле (3), найдем A= 3,98 мкДж.

2-й случай. Пластины остаются подключенными к источнику тока и система двух пластин уже не является изолированной (заряд с пластин при их раздвижении перемещается к клеммам батареи). Поэтому воспользоваться законом сохранения энергии в этом случае нельзя.

Заметим, что при раздвижении пластин конденсатора: а) разность их потенциалов остается неизменной (U= E); б) емкость будет уменьшаться (С= ε₀S/d). Будут уменьшаться также заряд на пластинах (Q=CU)и напряженность электрического поля (Е = U/d).Так как величины Е и Q, необходимые для определения работы, изменяются, то работу следует вычислять путем интегрирования.

Напишем выражение для элементарной работы:

dA=QE₁dx, (4)

где E₁- напряженность поля, создаваемого зарядом одной пластины.

Выразим напряженность поля E₁и заряд Q через расстояние х между пластинами:

E₁= 1/2Е = E/ 2х и Q = C E, или Q = ε₀SE/x.

Подставив эти выражения E₁и Q в равенство (4), получим

dA= 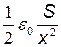E²dx.

Проинтегрировав это равенство в пределах от d₁ до d₂,найдем выражение искомой работы:

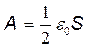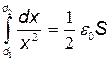E ² 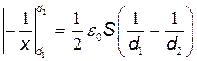E ² E ².

После упрощений последняя формула примет вид

A=ε₀S E ²(d₂ – d₁)/(2d₁d₂).

Сделав вычисления по полученной формуле, найдем

А=1,33мкДж.

Пример 24. Плоский конденсатор заряжен до разности потенциалов U= 1 кВ. Расстояние d между пластинами равно 1 см. Диэлектрик – стекло ( 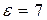). Определить объемную плотность энергии поля конденсатора.

Решение. Объемная плотность энергии поля конденсатора

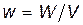,(1)

где W - энергия поля конденсатора; V- объем, занимаемый полем, т. е. объем пространства, заключенного между пластинами конденсатора.

Энергия поля конденсатора определяется по формуле

W=CU²/ 2,(2)

где U - разность потенциалов, до которой заряжены пластины конденсатора; С - его электроемкость. Но C=εε₀S/d, V=Sd. Подставив выражение С в формулу (2) и затем выражения W и V в формулу (1), получим

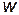=εε₀U²/ (2d²).

Подставив значения величин в последнюю формулу и вычислив, найдем

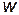=0,309 Дж/м³.

Пример 25. Металлический шар радиусом R=3cм несет заряд Q=20 нКл. Шар окружен слоем парафина ( 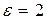) толщиной d=2см. Определить энергию W электрического поля,заключенного в слое диэлектрика.

Решение. Так как поле, созданное заряженным шаром, является неоднородным, то энергия поля в слое диэлектрика распределена неравномерно. Однако объемная плотность энергии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы так как поле заряженного шара обладает сферической симметрией.

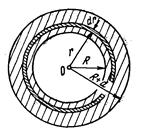Выразим энергию в элементарном сферическом слое диэлектрика объемом dV: dW=wdV,где w - объемная плотность энергии (рис. 39).

Полная энергия выразится интегралом

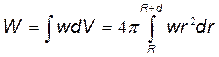, (1)

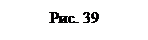где r- радиус элементарного сферического слоя; dr- его толщина. Объемная плотность энергии определяется по формуле w = εε₀Е²/2,где Е – напряженность поля. В нашем случае 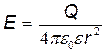и, следовательно,

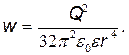
Подставив это выражение плотности в формулу (1) и вынеся за знак интеграла постоянные величины, получим

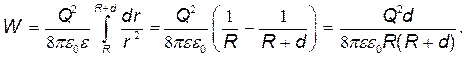
произведя вычисления по этой формуле, найдем

W=12 мкДж.

Пример 26. Определить заряд Q, прошедший по проводу с сопротивлением R=3Ом при равномерном нарастании напряжения на концах провода от U₀=2В до U =4В в течение t=20с.

Решение. Так как сила тока в проводе изменяется, то воспользоваться для подсчета заряда формулой Q=It нельзя. Поэтому возьмем дифференциал заряда dQ=Idt и проинтегрируем:

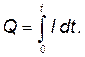(1)

Выразив силу тока по закону Ома, получим

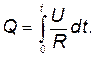(2)

Напряжение U в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой

U= U₀+kt, (3)

где k - коэффициент пропорциональности. Подставив это выражение U в формулу (2), найдем

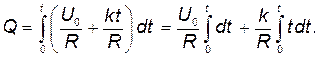
Проинтегрировав, получим

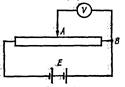
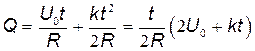. (4)

Значение коэффициента пропорциональности k найдем из формулы (3), если заметим, что при t= 20 с U=4В:

k=(U – U₀)/t=0,1B/c.

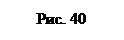Подставив значения величин вформулу (4), найдем

Q=20Кл.

Пример 27. Потенциометр с сопротивлением R= 100Ом подключен к источнику тока, ЭДС E которого равна 150 В и внутреннее сопротивление r = 50 Ом (рис. 40). Определить показание вольтметра с сопротивлением R_B=500Ом, соединенного проводником с одной из клемм потенциометра и подвижным контактом с серединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключенном вольтметре?

Решение. Показание U₁ вольтметра, подключенного к точкам А и В (рис. 40), определяется по формуле

U₁=I₁R₁, (1)

где I₁ - сила тока в неразветвленной, части цепи; R₁- сопротивление параллельно соединенных вольтметра и половины потенциометра.

Силу тока I₁ найдем по закону Ома для всей цепи:

I₁=E/(R+r), (2)

где R - сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

R=R/2+R₁. (3)

Сопротивление R₁параллельного соединения может быть найдено по формуле 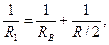откуда

R_l= RR_B/(R + 2R_B).

Подставив в эту формулу числовые значения величин и произведя вычисления, найдем

R_l=45,5Ом.

Подставив в выражение (2) правую часть равенства (3), определим силу тока:

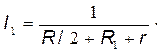E =1,03 А

Если подставить значения I₁ и R₁в формулу (1), то найдем показание вольтметра: U₁=46,9В.

Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I₂ на половину сопротивления потенциометра, т. е. U₂ =I₂(R/2),или 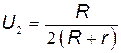·E.

Подставив сюда значения величин E, r и R получим

U₂=50В.

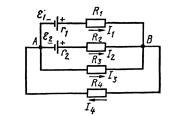
Пример 28. Источники тока с электродвижущими силами E₁и E₂включены в цепь, как показано на рис. 41. Определить силы токов, текущих в сопротивлениях R₂ и R₃, если E₁= 10 В иE₂=4В, а R₁=R₄=2 Оми R₂=R₃=4Ом. Сопротивлениями источников тока пренебречь.

Решение. Силы токов в разветвленной цепи определяют с помощью законов Кирхгофа. Чтобы найти четыре значения силы токов, следует составить четыре уравнения.

Перед составлением уравнений по закону Кирхгофа необходимо, во-первых, выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать направление обхода контуров (последнее только для составления уравнений по второму закону Кирхгофа).

Выберем направления токов, как они показаны на рис. 41, и условимся обходить контуры по часовой стрелке.

Рассматриваемая в задаче схема имеет два узла: А и В. Но составлять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.

При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, - со знаком минус.

По первому закону Кирхгофа для узла В имеем

I₁+I₂+I₃ – I₄=0.

Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовавшая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлением обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус,

б) если ЭДС повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае - со знаком минус.

По второму закону Кирхгофа имеем соответственно для контуров AR₁BR₂A, AR₁BR₃A, AR₃BR₄A:

I₁R₁ – I₂R₂=E₁ – E₂ ,(1)

I₁R₁ – I₃R₃=E₁ , (2)

I₃R₃ + I₄R₄=0. (3)

Подставив в равенства (1)-(3) значения сопротивлений и ЭДС, получим систему уравнений:

I₁+I₂+I₃ – I₄=0,

2I₁-4I₂=6,

2I₁-4I₃=10,

4I₃+2I₄=0.

Поскольку нужно найти только два тока, то удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения еще раз в следующем виде:

I₁+I₂+I₃-I₄=0,

2I₁-4I₂+0+0=6,

2I₁+0-4I₃+0=10,

0+0+4I₃+2I₄=0.

Искомые значения токов найдем из выражений

I₂=Δ_I2/Δи I₃=Δ_I3/Δ,

где Δ- определитель системы уравнений; Δ_I2и Δ_I3 - определители, полученные заменой соответствующих столбцов определителя 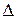столбцами, составленными из свободных членов четырех вышеприведенных уравнений, находим

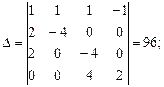
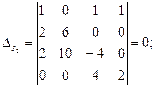
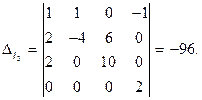
Отсюда получаем

I₂=0; I₃ = -1 А.

Знак минус у значения силы тока I₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I₃было указано противоположно истинному. На самом деле ток I₃ течет от узла В к узлу А.

Пример 29. Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному закону от I₀=0 до I_max=6 А (рис. 42). Определить количество теплоты Q₁, выделившееся в этом проводнике за первую секунду, и Q₂ - за вторую, а также найти отношение этих количеств теплоты Q₂/Q₁.

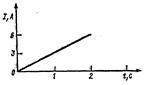Решение. Закон Джоуля - Ленца Q=I²Rt применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

dQ= I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В нашем случае

I=kt, (2)

где k - коэффициент пропорциональности, равный отношению приращения силы тока к интервалу времени, за который произошло это приращение:

k=ΔI/Δt=3 А/с.

С учетом равенства (2) формула (1) примет вид

dQ=k²Rt²dt. (3)

Для определения количества теплоты, выделившегося за конечный промежуток времени Δt,выражение (3) следует проинтегрировать в пределах от t₁до t₂:

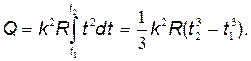
При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t₁=0, t₂= 1 с и, следовательно,

Q₁=60 Дж,

а за вторую секунду - пределы интегрирования t₁= 1 с, t₂=2с и тогда

Q₂=420 Дж.

Следовательно,

Q₂/Q₁=7,

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.

Таблица вариантов

Контрольная работа № 3

Вариант	Номера задач

Задачи

1. Три одинаковых точечных заряда нКл находятся в вершинах равностороннего треугольника со стороной а=10 см. Определить модуль и направление силы, действующей на один из зарядов со стороны двух других.

2. Два положительных точечных заряда 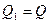и 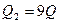закреплены на расстоянии d=100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

3. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол 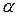. Шарики погружают в масло. Какова плотность масла ρ, если угол расхождения нитей при погружении в масло остается тем же? Плотность материала шариков 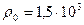кг/м³, диэлектрическая проницаемость масла ε=2,2.

4. В вершинах квадрата находятся одинаковые заряды 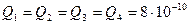Кл. Какой отрицательный заряд нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

5. Тонкий стержень длиной l=10 см равномерно заряжен с линейной плотностью заряда τ=1 мкКл/м.На продолжении оси стержня на расстоянии d=20 см от ближайшего его конца находится точечный заряд 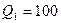нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.