Классическая вероятностная модель. Геометрическая вероятность
Построение графиков
Графики любых функций строят по точкам. Но если вид графика заранее неизвестен, эти точки надо выбирать со смыслом — выделять особо важные точки графика, которые определяют его вид.
Теория:
Если речь идет о построении графика незнакомой функции, когда заранее невозможно представить вид графика, полезно применять определенную схему исследования свойств функции, которая помогает составить представление о ее графике. Когда такое представление сложится, можно приступать к построению графика по точкам.
В курсе математического анализа разработана универсальная схема исследования свойств функции и построения графика функции, позволяющая строить весьма сложные графики. Для наших нужд будут достаточны упрощенные варианты указанной схемы.
1) Если функция y=f(x) непрерывна на всей числовой прямой, то достаточно найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек.
2) Если функция y=f(x) определена не на всей числовой прямой, то начинать следует с нахождения области определения функции (если область не задана) и с указания ее точек разрыва.
3) Полезно исследовать функцию на чётность, поскольку графики четной или нечетной функций обладают симметрией (соответственно относительно оси y или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при x>0, а затем дорисовать симметричную ветвь.
4) Если limx→∞f(x)=b , то, как известно, прямая y=b является горизонтальной асимптотой графика функции y=f(x). Асимптоту следует строить на координатной плоскости, она дает своеобразный ориентир для графика.
5) При условии: если x→a, то y→∞ — прямая x=a является вертикальной асимптотой графика функции y=f(x).
Пример:
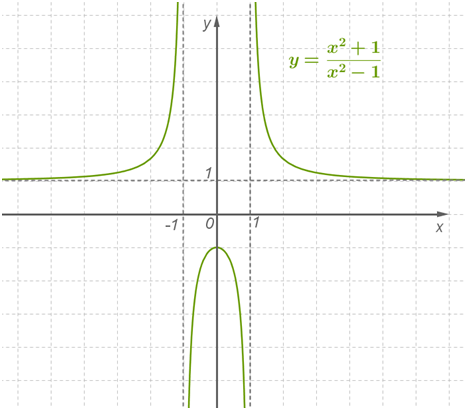
Построить график функции y=x2+1x2−1.
Решение 1. Введем обозначение: f(x)=x2+1x2−1. Найдем область определения функции. Она задается условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).
2. Исследуем функцию на чётность:
f(−x)=(−x)2+1(−x)2−1=x2+1x2−1=f(x)
Значит, заданная функция чётна, ее график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.
3. Найдём асимптоты. Вертикальной асимптотой является прямая x=1, поскольку при этом значении x знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):
limx→∞x2+1x2−1=limx→∞x2x2+1x2x2x2−1x2=limx→∞1+1x21−1x2=1
Значит, y=1 — горизонтальная асимптота графика функции.
4. Найдем стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y′=(x2+1x2−1)′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′(x2−1)2=2x⋅(x2−1)−(x2+1)⋅2x(x2−1)2=−4x(x2−1)2.
Производная существует всюду в области определения функции, значит, критических точек у функции нет.
Стационарные точки найдем из соотношения y′=0. Получаем: −4x=0, откуда находим, что x=0. При x<0 имеем:y′>0 ; при x>0 имеем: y′<0. Значит, x=0 — точка максимума функции, причем ymax=f(0)=02+102−1=−1.
При x>0 имеем: y′<0; но следует учесть наличие точки разрыва x=1. Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке [0;1) функция убывает, на промежутке (1;+∞)функция также убывает.
5. Составим таблицу значений функции f(x)=x2+1x2−1 при x≥0:
| x | 0.5 | ||||
| y | −1 | −53 |
6. Отметив найденные точки на координатной плоскости, учтя при этом, что(0;−1) — точка максимума, что y=1 —горизонтальная асимптота, что x=1 —вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график:
Теория вероятностей
Теория:
Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).
Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).
Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.
События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... .
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A.
Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.
Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.
Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.
Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.
Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
Рассмотрим следующий пример. Будем следить за движением какой-нибудь определенной молекулы газа, заключенного в некоторый объем. Внутри этого объема выделим объемы  и и  , частично перекрывающие друг друга. Пусть событие A — попадание молекулы в объем , частично перекрывающие друг друга. Пусть событие A — попадание молекулы в объем  , событие В — попадание молекулы в объем , событие В — попадание молекулы в объем 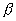 . Совмещением событий A и В является попадание молекулы в общую часть объемов . Совмещением событий A и В является попадание молекулы в общую часть объемов 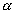 и и 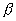 . Если объемы . Если объемы 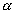 и и 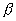 не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем 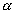 или только в объем или только в объем 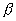 , или же в их общую часть. , или же в их общую часть. |
Задачи:
Комбинаторика
Задача 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать?
Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т. е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно N=n1´n2´n3=30´29´28=24360.
Задача 5. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т. е. является перестановкой из 7 элементов. Их число равно
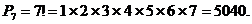
Классическая вероятностная модель. Геометрическая вероятность
Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут.
Решение. Вначале подсчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел и имеет n1=10 возможностей, второй тоже имеет n2=10 возможностей, наконец, третий также имеет n3=10 возможностей. В силу правила умножения общее число способов равно: n= n1´n2´n3=103 = 1000, т. е. все пространство содержит 1000 элементарных исходов. Для вычисления вероятности события A удобно перейти к противоположному событию, т. е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет m1=10 способов выбора числа. Второй студент имеет теперь лишь m2=9 возможностей, поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента. Третий студент еще более ограничен в выборе — у него всего m3=8 возможностей. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно m=10×9×8=720. Случаев, в которых есть совпадения, остается 280. Следовательно, искомая вероятность равна Р=280/1000= 0,28.
3. Основные формулы теории вероятностей
Задача 2. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.
Решение. Обозначим через A, B и С события, заключающиеся в том, что случайно выбранный сотрудник фирмы владеет английским, немецким или французским соответственно. Очевидно, доли сотрудников фирмы, владеющих теми или иными языками, определяют вероятности этих событий. Получаем:
а) P(AÈB)=P(A)+P(B) -P(AB)=0,28+0,3-0,08=0,5;
б) P(AÈBÈC)=P(A)+P(B)+P(C)-(P(AB)+P(AC)+P(BC))+P(ABC)=0,28+0,3+0,42-
-(0,08+0,1+0,05)+0,03=0,8;
в) 1-P(AÈBÈC)=0,2.
Случайная величина
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Примеры случайных величин:
1) число попаданий при трех выстрелах;
2) число вызовов, поступавших на телефонную станцию за сутки;
3) частота попадания при 10 выстрелах.
Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.
Так, в примере 1) эти значения:
0, 1, 2, 3;
в примере 2):
1,2, 3, 4, …;
в примере 3)
0; 0,1; 0,2; …; 1,0.
Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.
Существуют случайные величины другого типа, например:
1) абсцисса точки попадания при выстреле;
2) ошибка взвешивания тела на аналитических весах;
3) скорость летательного аппарата в момент выхода на заданную высоту;
4) вес наугад взятого зерна пшеницы.
Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще – границы неопределенные, расплывчатые.
Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.
Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая»теория вероятностей оперировала по преимуществу с событиями, то современная теория вероятностей предпочитает, где только возможно, оперировать со случайными величинами.
Приведем примеры типичных для теории вероятностей приемов перехода от событий к случайным величинам.
Производится опыт, в результате которого может появиться или не появиться некоторое событие 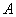 . Вместо события
. Вместо события 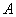 можно рассмотреть случайную величину
можно рассмотреть случайную величину 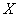 , которая равна 1, если событие
, которая равна 1, если событие 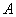 происходит, и равна 0, если событие
происходит, и равна 0, если событие 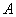 не происходит. Случайная величина
не происходит. Случайная величина 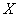 , очевидно, является прерывной; она имеет два возможных значения: 0 и 1. Эта случайная величина называется характеристической случайной величиной события
, очевидно, является прерывной; она имеет два возможных значения: 0 и 1. Эта случайная величина называется характеристической случайной величиной события 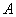 . На практике часто вместо событий оказывается удобнее оперировать их характеристическими случайными величинами. Например, если производится ряд опытов, в каждом из которых возможно появление события
. На практике часто вместо событий оказывается удобнее оперировать их характеристическими случайными величинами. Например, если производится ряд опытов, в каждом из которых возможно появление события 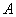 , то общее число появлений события равно сумме характеристических случайных величин события
, то общее число появлений события равно сумме характеристических случайных величин события  во всех опытах. При решении многих практических задач пользование таким приемом оказывается очень удобным.
во всех опытах. При решении многих практических задач пользование таким приемом оказывается очень удобным.
С другой стороны, очень часто для вычисления вероятности события оказывается удобно связать это событие с какой-то непрерывной случайной величиной (или системой непрерывных величин).
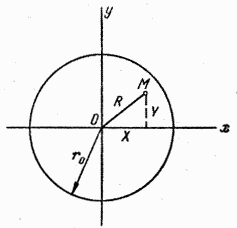
Рис. 2.4.1.
Пусть, например, измеряются координаты какого-то объекта О для того, чтобы построить точку М, изображающую этот объект на панораме (развертке) местности. Нас интересует событие  , состоящее в том, что ошибка R в положении точки М не превзойдет заданного значения
, состоящее в том, что ошибка R в положении точки М не превзойдет заданного значения  (рис. 2.4.1). Обозначим
(рис. 2.4.1). Обозначим 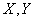 случайные ошибки в измерении координат объекта. Очевидно, событие
случайные ошибки в измерении координат объекта. Очевидно, событие 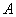 равносильно попаданию случайной точки М с координатами
равносильно попаданию случайной точки М с координатами 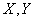 в пределы круга радиуса
в пределы круга радиуса 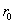 с центром в точке О. Другими словами, для выполнения события
с центром в точке О. Другими словами, для выполнения события 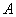 случайные величины
случайные величины 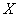 и
и 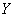 должны удовлетворять неравенству
должны удовлетворять неравенству
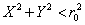 . (2.4.1)
. (2.4.1)
Вероятность события 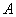 есть не что иное, как вероятность выполнения неравенства (2.4.1). Эта вероятность может быть определена, если известны свойства случайных величин
есть не что иное, как вероятность выполнения неравенства (2.4.1). Эта вероятность может быть определена, если известны свойства случайных величин 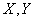 .
.
Такая органическая связь между событиями и случайными величинами весьма характерна для современнойтеории вероятностей, которая, где только возможно, переходит от «схемы событий» к «схеме случайных величин». Последняя схема сравнительно с первой представляет собой гораздо более гибкий и универсальный аппарат для решения задач, относящихся к случайным явлениям.
Примеры:
Задача 1. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.
Решение. Возможные значения величины X: x1 = 0; x2 = 10 и x3 = 50. Так как «пустых» билетов – 89, то p1 = 0,89, вероятность выигрыша 10 у.е. (10 билетов) – p2 = 0,10 и для выигрыша 50 у.е. – p3 = 0,01. Таким образом:
| X | |||
| P | 0,89 | 0,10 | 0,01 |
Легко проконтролировать: 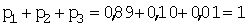 .
.
Задача 2. Вероятность того, что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее. Составить ряд распределения количества опрошенных покупателей.
Решение. Согласно условию задачи р = 0,6. Откуда: q=1-p = 0,4. Подставив данные значения, получим: 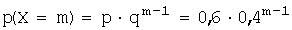 и построим ряд распределения:
и построим ряд распределения:
| Х | … | m | … | ||
| pi | 0,6 | 0,24 | … | 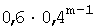 | … |
Задача 3. Компьютер состоит из трех независимо работающих элементов: системного блока, монитора и клавиатуры. При однократном резком повышении напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения Бернулли составить закон распределения числа отказавших элементов при скачке напряжения в сети.
Решение. Рассмотрим распределение Бернулли (или биномиальное): вероятность того, что в n испытаниях событие А появится ровно k раз: 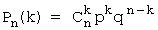 , или:
, или:
| X | … | k | … | n | ||
| P | qn | 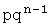 | … | 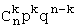 | … | pn |
Вернёмся к задаче.
Возможные значения величины X (число отказов):
x0 =0 – ни один из элементов не отказал;
x1 =1 – отказ одного элемента;
x2 =2 – отказ двух элементов;
x3 =3 – отказ всех элементов.
Так как, по условию, p = 0,1, то q = 1 – p = 0,9. Используя формулу Бернулли, получим
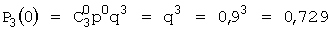 ,
, 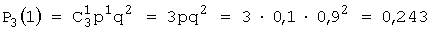 ,
,
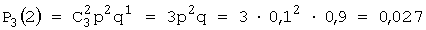 ,
, 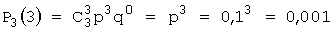 .
.
Контроль: 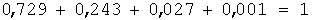 .
.
Следовательно, искомый закон распределения:
| X | ||||
| p | 0,729 | 0,243 | 0,027 | 0,001 |
Численное интегрирование
Теория:Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма 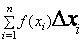 при стремлении всех промежутков ∆xi к нулю
при стремлении всех промежутков ∆xi к нулю
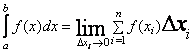
При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: 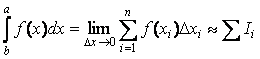 , где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
, где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
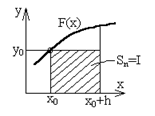
Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника
 , где h - шаг интегрирования, у0 - значение функции в точке х=х0
, где h - шаг интегрирования, у0 - значение функции в точке х=х0
у(х0)=у0
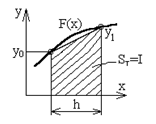
Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной суммы как площадь трапеции
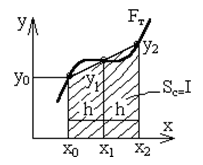
Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде
y(x)=y0A0(x)+y1A1(x)+y2A2(x), где
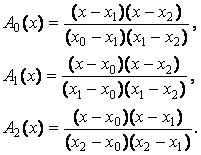
При x0=0; x1=h; x2=2h, получим


При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид
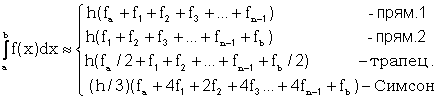
где h - шаг по x, fa, fi, fb - значения функции при x равном a, xi, b соответственно. Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников.
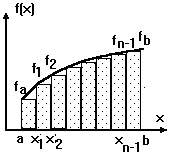
Рис. Численное интегрированние методом прямоугольников
