Сумма токов входящих равна сумме токов выходящих для каждого узла.

.

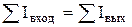Это можно сформулировать иначе:

Алгебраическая сумма токов, сходящихся в узле, равна нулю ( 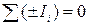), причем токи, входящие в узел, берутся со знаком минус, а выходящие из него – со знаком плюс.

Сформулированный закон является прямым следствием закона сохранения электрического заряда. Он формулирует условия, необходимые для того, чтобы заряд не накапливался в узле.

2-й закон Кирхгофа справедлив для любого контура разветвленной цепи.

Сумма (алгебраическая) ЭДС равна алгебраической сумме падений напряжения на всех элементах данного контура:

,

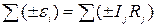где ток, текущий по сопротивлению.

Правило знаков подразумевает, что произвольно выбирается направление обхода контура:

· ЭДС > 0. Если при обходе контура ЭДС проходится от «–» к «+» движение в направлении действия сторонней силы, то в противоположном случае ЭДС берется со знаком минус;

· аналогично знаком падения напряжения выбирается «+», если ток в элементе контура совпадает с направлением обхода контура, и «–» в противном случае .

Рекомендации по практическому применению. Перед применением правил Кирхгофа необходимо расставить токи на схеме цепи. Для этого в каждой ветви необходимо указать направление тока стрелкой и ввести его буквенное обозначение. При этом стрелку можно ставить в произвольном направлении, поскольку в сложной цепи направление токов может меняться в зависимости от параметров цепи, и угадать истинное направление бывает невозможно. Если ток течет в направлении, противоположном стрелке, то в результате решения уравнений Кирхгофа соответствующий ток будет иметь отрицательное значение.

Если цепь имеет N узлов, первое правило Кирхгофа необходимо записать для N-1 узла. Последнее уравнение будет являться следствием уже известных. Остальные независимые уравнения могут быть получены с использованием второго закона Кирхгофа. При этом каждый новый контур, для которого применяется этот закон, должен содержать хотя бы одну новую ветвь, не входящую в другие контуры.

Если придерживаться этих рекомендаций, то число полученных независимых уравнений будет равно числу ветвей цепи или числу токов. Для определения неизвестных токов по заданным характеристикам элементов цепи необходимо решить линейную алгебраическую систему уравнений. Число уравнений равно числу неизвестных и равно числу ветвей. Решение этой задачи не представляет принципиальных трудностей (например, можно решать уравнения методом Крамера). Таким образом, законы Кирхгофа позволяют рассчитать произвольную разветвленную цепь.

Пример расчета разветвленной схемы, изображенной на рис.6.1. Предположим, заданы значения ЭДС источников и сопротивления всех элементов. Необходимо определить токи во всех ветвях.

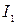
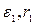
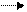
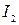
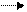
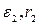
А Б

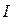
R

Рис.6.1

1. Расставляем стрелки направлений токов в каждой ветви (направления произвольные) и вводим буквенные обозначения токов, как это показано на рисунке.

2. Схема содержит два узла. Для узла «А» применяем первое правило Кирхгофа: 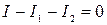. Если применить это правило для узла «Б», то получим то же самое соотношение, умноженное на –1, поэтому недостающие два соотношения для определения трех неизвестных токов можно получить, пользуясь вторым правилом – для контуров.

3. Выберем замкнутый контур А- 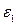-Б –R –А и направление его обхода по часовой стрелке (выбирается произвольно). Применим для него второе правило Кирхгофа: 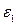= 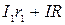. ЭДС имеет знак «+» поскольку при движении внутри источника приходится от отрицательной к положительной клемме. Вторым возьмем контур А- R – Б - 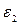- А и обойдем его против часовой стрелки. Второе правило Кирхгофа в этом случае приводит к соотношению: .

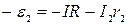4. Решаем полученные уравнения относительно неизвестных токов и в результате получаем ответ для любых значений элементов цепи (для краткости записи обозначим ):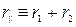

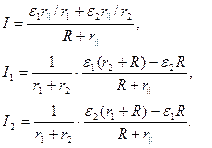
Видим, что токи, текущие через источники, могут менять направление (знак) в зависимости от параметров цепи, поэтому угадать, как нужно ставить стрелки, до решения задачи не возможно.

Из первой формулы следует, что батарею из двух параллельно присоединенных источников тока можно заменить одним источником со следующими параметрами:

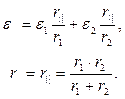
Действительно, если заменить батарею одним источником, то схема будет иметь вид, изображенный на рис. 4.1. Поскольку она неразветвленная, ток через сопротивление R можно выразить формулой: 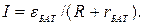Если взять 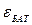и 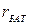в соответствии с полученными формулами, в этом случае батарея будет давать такой же ток, равный I, который дают два параллельно подключенных источника тока.