Тема 2. «тяговый расчет горной

ГУСЕНИЧНОЙ МАШИНЫ»

2.1. Основные расчетные зависимости

Тяговый расчет гусеничной машины посвящен определению затрат мощности, необходимой для передвижения машины при заданной скорости, и проверке условий возможности передвижения. Расчет выполняется при движении машины по прямой и при совершении статического поворота.

Мощность для движения машины по прямой

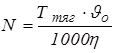, (2.1)

где 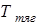- суммарное тяговое усилие обеих гусеничных лент (окружное

усилие на ведущих звездочках);

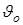- кинематическая скорость движения;

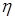- коэффициент полезного действия передач от двигателя к

ведущим звездочкам гусеничного хода.

Тяговое усилие гусеничных цепей уравновешивает силы сопротивления движению:

,

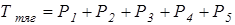где 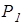- сила сопротивления деформированию несущего основания;

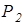- сила сопротивления движению опорных катков гусеничного

хода по гусеничным цепям;

- сила сопротивления движению прицепной машины;

- сила сопротивления от составляющей силы тяжести при
движении машины в гору;

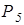- сила сопротивления движению, обусловленная силами инерции
при разгоне (трогании с места) агрегата.

Составляющие суммарного тягового усилия вычисляются по формулам:

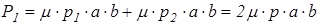, (2.2)

где 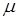- коэффициент сопротивления мятию грунта;

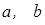- размеры опорной площади гусениц;

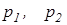- давление под левой и правой гусеницами;

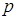- среднее давление машины на опорное основание.

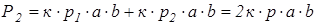, (2.3)

где 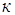- коэффициент сопротивления движению опорных катков по

гусеничным цепям.

, (2.4)

где 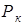- крюковое усилие (усилие в сцепке).

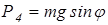, (2.5)

где 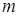- масса тягача;

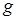- ускорение силы тяжести;

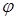- угол наклона опорной поверхности (угол продольного крена).

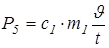, (2.6)

где 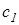- коэффициент, учитывающий затраты мощности на разгон

вращающихся масс трансмиссии;

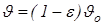- действительная скорость передвижения;

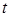- время разгона машины;

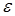- коэффициент буксования.

Коэффициент 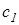можно принимать равным 1,1, а время разгона 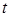составляет 6-12 с.

Условия возможности передвижения по прямой заключаются в выполнении соотношений:

(2.7)

где 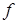- коэффициент трения между гусеничными цепями и грунтом;

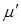- часть коэффициента сопротивления мятию, соответствующая

силам сопротивления мятию, дающим внешнюю составляющую.

Первое соотношение (2.7) выражает условие достаточности мощности двигателя, а второе – достаточности сцепления гусениц с грунтом. Физический смысл первого условия очевиден. Для выяснения физического смысла второго условия рассмотрим силы, действующие на гусеничную цепь при движении по прямой.

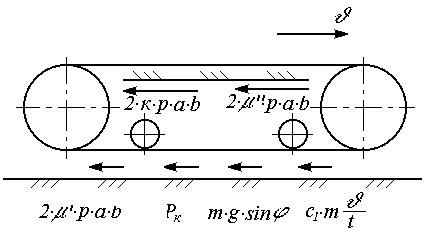На рис. 2.1 показаны силы, действующие на обе гусеничные ленты. Из схемы видно, что часть сил сопротивления проявляется как внешние силы, т.е. действуют на гусеничную машину в целом, а другая часть – обусловлена сопротивлением движению в самом гусеничном движителе (сила .

Рис. 2.1. Схема сил, действующих на гусеничные цепи

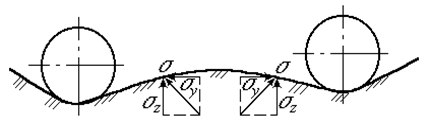К внутренним силам относится также часть силы сопротивления деформирования грунта, соответствующая горизонтальным составляющим сил сопротивления мятию. Поясним это, рассмотрев деформацию грунта между двумя соседними опорными катками (рис. 2.2).

Рис. 2.2. К выяснению физического смысла коэффициентов 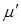и

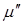
Напряжение 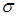сопротивления деформированию несущего основания для пассивного гусеничного хода направлено нормально к поверхности гусеничной цепи. Разложим это напряжение на составляющие по осям 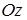и 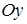и просуммируем их по всей опорной поверхности. Заменяя суммы интегралами и учитывая равновесие самохода в вертикальной плоскости, получим

.

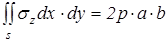Кроме того, учитывая направление составляющих 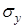можно записать (рис. 2.2)

.

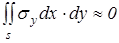Поэтому часть силы сопротивления мятию грунта, обусловленная составляющими 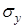напряжений сопротивления деформированию является внутренней силой и учитывается коэффициентом .

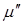В связи с этим возможность передвижения машины сцеплению с грунтом ограничена силами сопротивления, стоящими в правой части второго соотношения (2.7).

При проведении тягового расчета гусеничной машины на повороте определяются радиус и угловая скорость поворота, тяговые усилия гусеничных лент и мощность, необходимая для совершения поворота, а также проверяются условия возможности его выполнения. Решение этих задач требует нахождения положения центров вращения опорных ветвей гусеничных цепей [2], которое в системе координат, связанной с машиной, определяется их смещениями 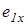, , 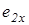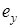относительно геометрических центров опорных площадей гусениц (рис. 2.3).

Для определения радиуса и угловой скорости поворота машины рассмотрим ее движение как сложное, состоящее из переносного и относительного. За переносное движение примем движение опорных ветвей относительно поверхности грунта, а за относительное – движение корпуса относительно опорных ветвей. На основании теоремы о сложении скоростей в сложном движении запишем

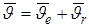, (2.8)

где 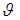- абсолютная скорость;

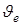- переносная (скорость скольжения цепей по залежи);

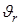- относительная.

В точках 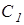и - центрах вращения опорных ветвей гусеничных лент – переносная скорость равна нулю. Поэтому для точек корпуса машины, совпадающих с точкам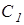и и , выражение (2.8) примет вид

.

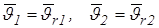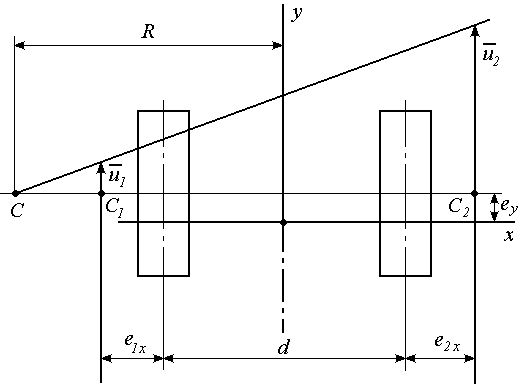Рис. 2.3. Положение центров вращения опорных ветвей гусениц

и кинематика поворота

Относительные скорост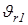и и 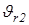корпуса равны скоростям перематывания гусеничных лент 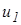и 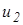, а их направление совпадает с осью 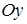. Таким образом, зная скорост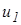и и 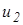перематывания гусеничных цепей и смещения 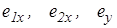центров вращения их опорных ветвей мы знаем скорости двух точек корпуса машины. Так как движение корпуса можно считать плоскопараллельным, то это позволяет определить радиус и угловую скорость поворота

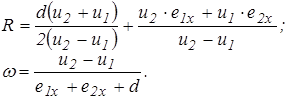(2.9)

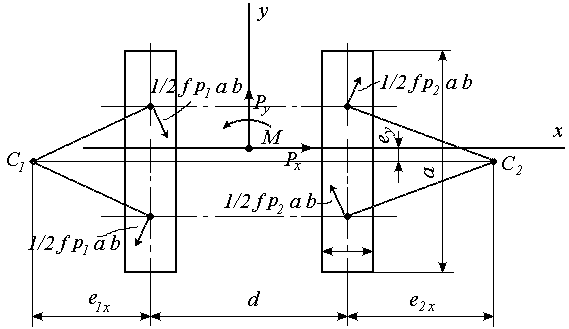Смещения центров вращения определяются из уравнений равновесия гусеничного хода на повороте, которые (рис. 2.4) имеют вид:

Рис. 2.4. К составлению уравнений равновесия

гусеничного хода при повороте

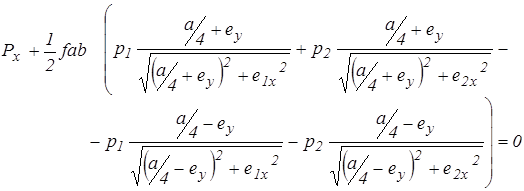
(2.10)

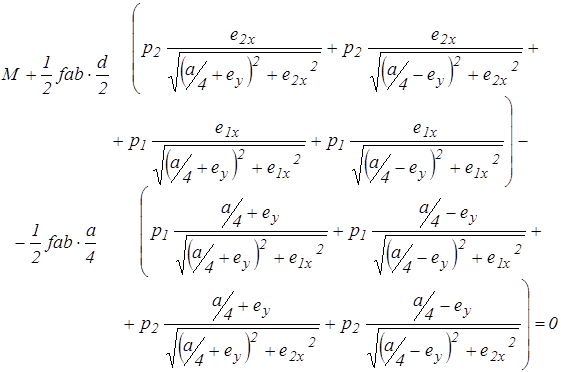
При составлении уравнений (2.10) внешние силы приведены к началу координат и выражены составляющим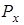и и главного вектора и главным моментом 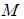. Распределенные силы трения опорных ветвей гусениц о поверхность грунта приведены к центрам середин опорных площадей гусеничных лент, т.е. заменены сосредоточенными.

Вследствие нелинейности уравнений (2.10) точные значения смещений 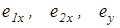найти можно только в некоторых частных случаях [2]. Поэтому для их нахождения обычно пользуются приближенными способами. При сравнительно небольших значениях силы 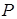и момента 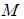смещения 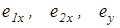можно определить по формулам:

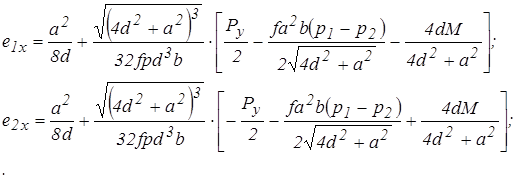(2.11)

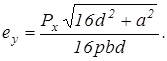(2.12)

Более удобно и правильно вычислять 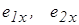и по специальной программе, имеющейся в составе ПО кафедры «Горные машины» и реализующей метод скорейшего спуска решения систем нелинейных уравнений.

Исходные данные для работы программы, включающие конструктивные параметры 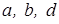, внешние сдвигающие нагрузки 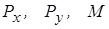давления под гусеницами 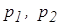, коэффициент трения между гусеницами и грунтом 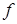вводятся по запросу программы с клавиатуры. После определения 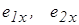и целесообразно произвести проверку решения, для чего полученные значения необходимо подставить в уравнения (2.10).

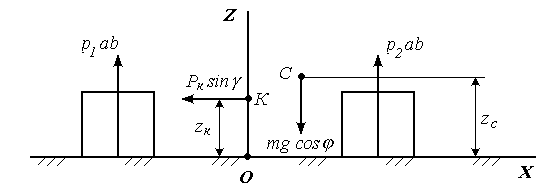
Внешние нагрузки 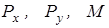и давления 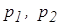под гусеницами при движении гусеничного хода по горизонтальной плоскости вычисляются (рис. 2.5) с учетом крюковой нагрузки по формулам:

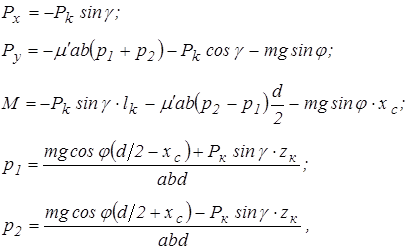(2.13)

где 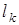- расстояние от центра опорной площади до сцепки;

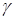- угол между осью 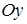и направлением действия крюкового усилия;

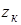- высота сцепки.

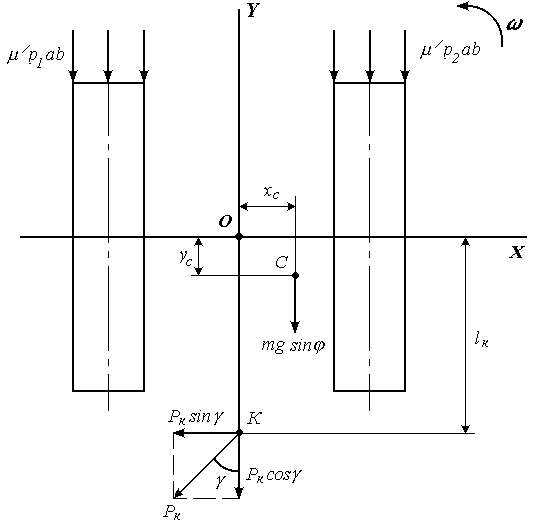Рис. 2.5. Схема для определения внешних нагрузок и давлений

под гусеницами

Тяговые усилия гусеничных лент при повороте (рис. 2.6):

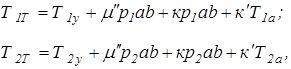(2.14)

где - продольные составляющие сил трения между гусеницами
и грунтом;

- арифметические суммы боковых сил, действующих на
гусеничные цепи;

- коэффициент сопротивления движению опорных катков
по гусеничным цепям за счет действия боковых сил
(учитывают потери на трение между боковыми
поверхностями катков и направляющими гусеничных
цепей).

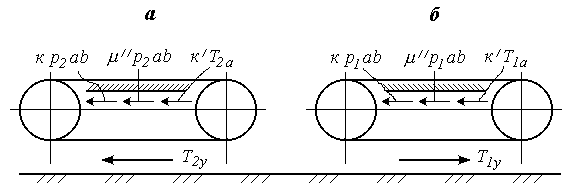Рис. 2.6. К определению тяговых усилий гусеничных цепей при повороте:

а – забегающая гусеница; б – отстающая гусеница.

Продольные составляющие сил трения гусениц о грунт и арифметические суммы боковых сил вычисляются по приближенным формулам:

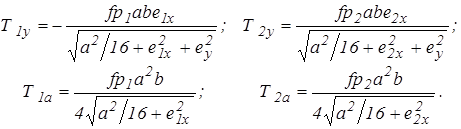(2.15)

При положительном значении смещения 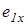сила 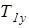отрицательна. Вследствие этого тяговое усилие отстающей гусеницы также может быть отрицательным. Физически это означает, что отстающая гусеница будет перематываться за счет сил трения, действующих на нее со стороны грунта. В этом случае для выполнения крутых поворотов отстающую гусеницу нужно тормозить.

Мощность, необходимая для выполнения поворота, вычисляется в зависимости от знака 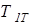. Если 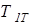>0, то мощность определяется по формуле

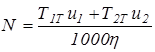. (2.16)

Если 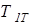<0, то

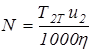, (2.17)

так как в этом случае отстающая гусеница тормозится и .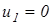

Для обеспечения возможности совершения поворота необходимо как и при прямолинейном движении выполнение двух условий. Первое из них выражает достаточность мощности двигателя и заключается в соблюдении соотношений

при положительном значении 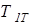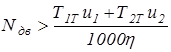(2.18)

и при отрицательном значении 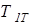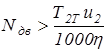(2.19)

Второе условие заключается в достаточности сцепления гусениц с грунтом. Это значит, что продольные составляющие сил трения между гусеницей и грунтом должны быть меньше предельных сил трения. С количественной точки зрения, второе условие характеризуется коэффициентом запаса сцепления, под которым понимается отношение предельной силы трения к ее продольной составляющей. Этот коэффициент вычисляется для обеих гусениц

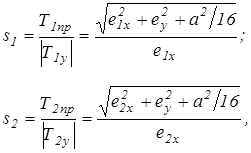(2.20)

где 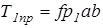, 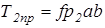- предельные значения сил трения.

Для обеспечения поворота необходимо, чтобы , .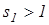

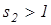В противном случае наступает полное буксование гусениц и движение прекращается. В том случае, когда 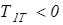необходимо знать тормозное усилие, которое нужно приложить к отстающей гусеничной цепи для ее остановки. Это усилие не должно быть меньшим, чем модуль тягового усилия, т.е.

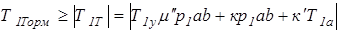. (2.21)

2.2. Порядок выполнения расчета

Расчет выполняется в два этапа. Сначала проводится тяговый расчет при движении по прямой. При этом расчете определяется среднее давление машины на грунт

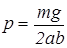
и по формулам (2.2-2.6) на основании исходных данных (см. приложение 2) вычисляются силы сопротивления передвижению и суммарное тяговое усилие гусеничных цепей. После этого определяется мощность на передвижение (формула 2.1). Применяя формулу (2.1), следует помнить, что единицей измерения суммарного тягового усилия и его составляющих служит «Н», а результат вычисления благодаря переводному коэффициенту «1000» получается в «кВт». Так как в исходных данных к заданию мощность двигателя не установлена, то проверка возможности передвижения производится только по второму соотношению (2.1).

Тяговый расчет машины при движении на повороте осуществляется в следующей последовательности:

- по формулам (2.13) вычисляются внешние сдвигающие нагрузки 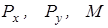и давления 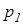и 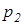под левой и правой гусеницами;

- определяются смещения 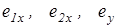центров вращения опорных ветвей гусеничных цепей (формулы 2.12) (более надежные результаты получаются при использовании программы, имеющейся в каталоге ПО кафедры);

- согласно выражений (2.15) находятся значения продольных составляющих 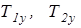сил трения и арифметические суммы боковых сил 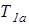и 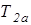, действующих на гусеницы;

- по формулам (2.14) определяются тяговые усилия 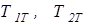гусеничных цепей.

Дальнейший порядок расчета определяется знаком тягового усилия на отстающей гусенице. Если 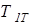>0, то радиус и угловая скорость поворота вычисляются по формулам (2.9), а мощность – по формуле (2.16). После этого для проверки возможности совершения поворота определяют коэффициенты запаса сцепления гусениц (формулы 2.20) и на этом расчет заканчивается.

Если 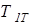<0, то радиус и угловую скорость поворота находят по формулам

; ,

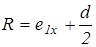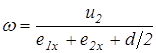мощность – по формуле (2.17) и заканчивают расчет определением коэффициентов запаса сцепления и тормозного усилия гусеничной цепи отстающей гусеницы.

Как при выполнении тягового расчета при движении по прямой проверка на достаточность мощности двигателя для совершения поворота не проводится. При использовании ПЭВМ для выполнения расчета смещения центров вращения опорных ветвей гусеничных лент определяются при помощи программы, реализующей метод скорейшего спуска для решения систем нелинейных уравнений. При этом исходные данные для работы программы готовятся вручную. Также вручную расчет заканчивается, т.е. после нахождения смещений центров вращения на ПЭВМ последующие величины определяются вручную.

Приложение 1