Статически неопределимые задачи продольного нагружения бруса

В статически неопределимых задачах расчета бруса при продольном нагружении одних уравнений статики недостаточно, поэтому необходимо использование дополнительных зависимостей, связанных с условиями совместности деформаций. Число таких дополнительных зависимостей соответствует степени статической неопределимости: s = n – m, где n – число реакций, а m – количество условий статики. В задачах продольного нагружения бруса число уравнений статики m = 1, т.е. 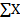= 0.

В статически неопределимых задачах продольного нагружения бруса выделяют два практических случая:

- продольное нагружение жестко закрепленного по концам бруса;

- совместное действие продольной нагрузки и изменение температуры для бруса (возможно наличие зазора между одним концом бруса и опорой).

Пример 3.3. Определить внутренние усилия, напряжения и деформации участков и всего бруса (рис.3.7.) при следующих исходных данных: ; ; ;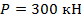

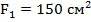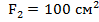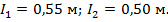
Решение

(3.4)

1. Определим степень статической неопределимости бруса. Всего неизвестных два (реакции опорных закреплений , см. рис. 3.6, а), а для системы сил, действующих по одной прямой, можно составить только одно уравнение статики: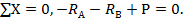

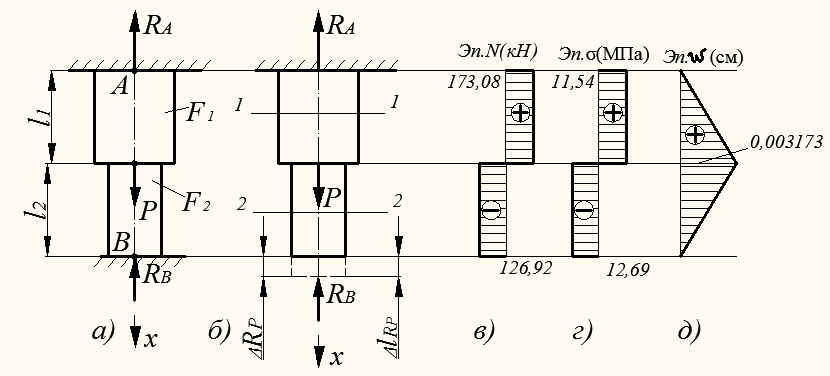
Рисунок 3.7 – Расчетная схема статически неопределимого бруса и эпюры элементов продольного нагружения

Следовательно, степень статической неопределимости системы равна: s = n – m = 2 – 1=1, т.е. система один раз статически неопределенна. Тогда для решения задачи необходимо составить одно дополнительное уравнение: например, отсутствие перемещения одного сечения бруса в т. В (см. 3.7, б).

Составляем дополнительное уравнение совместности деформаций из условия, что перемещение нижнего сечения бруса в т. В в основной системе должно быть равно нулю:

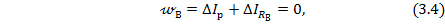
где 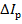– абсолютное перемещение этого сечения от действия внешней силы Р;

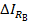– абсолютное перемещение бруса в основной системе от реакции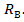

Абсолютное удлинение бруса от реакции 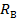равно:

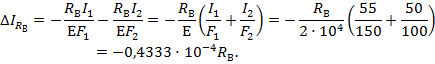
Тогда из условия совместности деформаций (3.4) получим уравнение:

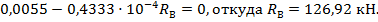
Из уравнения статики определяем другую реакцию :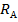

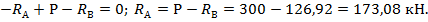
3. Используя метод сечений, находим величину продольных сил по участкам бруса:

- на участке I: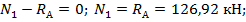

- на участке II: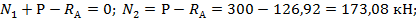

На основании выполненных расчетов строим эпюру продольных сил N (рис. 3.6, в).

4. Определим величину нормальных напряжений в поперечных сечениях бруса по участкам:

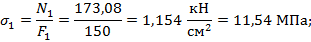
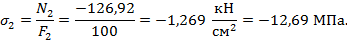
Строим эпюру нормальных напряжений σ (рис. 3.6,г).

5. Вычислим абсолютные деформации участков бруса:

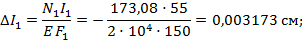
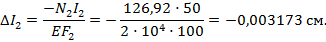
6. Определим перемещения границ участков относительно верхней жесткой заделки:

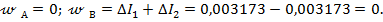
На основании выполненных расчетов строим эпюру перемещений (рис.3.7, д).

Пример 3.4. Стальной брус, жестко закрепленный обоими концами в неподвижных опорах (рис.3.8), нагревается на 40°С по сравнению с температурой, при которой был закреплен. Вычислить напряжения, возникающие в поперечных сечениях бруса при его нагреве. Исходные данные по брусу следующие: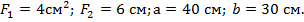

RD

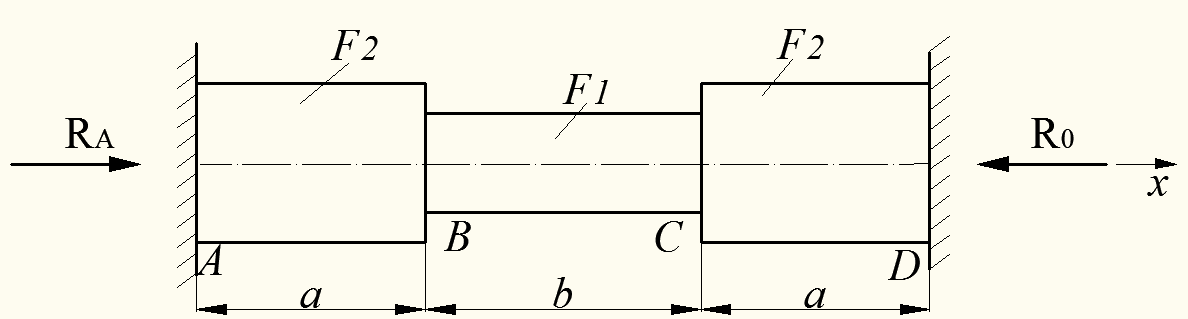
Рисунок 3.8 – Стальной брус со своими размерами

Решение

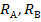В результате нагрева бруса в его закреплениях возникают реакции (см. рис. 3.8). Для их определения условие статики дает лишь одно уравнение: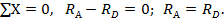

Отсюда нельзя определить величины реакций и задача становится статически неопределимой. Поэтому дальнейший ход решения задачи аналогичен предыдущему примеру 3.3.

Отбрасываем правую заделку и заменяем ее действием на брус искомой реактивной силой .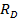

(3.5)

Перемещение сечения в точке D при отброшенной заделке определяется по выражению:

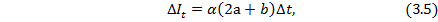
где α – коэффициент теплопроводности, который для стали на основании справочных данных принимается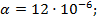

– температура нагрева бруса,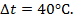

p 0mV0Pk2mQ/2PIPzYigNIXg0MPAnUSIczr2ST0dnYfz4MSz1pr3QRZMekGmTMWOk9i564gULX533o WhwY8BTnUNwgrwaGGcedRKEG85WSDuc7o/bLhhlBiXqjsTfzeDLxCxGUCRKLijm25McWpjlCZdRR MogrF5bI563hAntYysDvQyb7nHFuA+37HfOLcawHr4c/wfIPAAAA//8DAFBLAwQUAAYACAAAACEA xyBivuAAAAAJAQAADwAAAGRycy9kb3ducmV2LnhtbEyPzU7DMBCE70i8g7VI3KiTqH8J2VQIRG8I NaC2Rydekoh4HcVuG3h6zAmOoxnNfJNvJtOLM42us4wQzyIQxLXVHTcI72/Pd2sQzivWqrdMCF/k YFNcX+Uq0/bCOzqXvhGhhF2mEFrvh0xKV7dklJvZgTh4H3Y0ygc5NlKP6hLKTS+TKFpKozoOC60a 6LGl+rM8GQRXR8v967zcHyq5pe9U66fj9gXx9mZ6uAfhafJ/YfjFD+hQBKbKnlg70SOs4kX44hHm 6QpECKyjRQyiQkiTBGSRy/8Pih8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMA AAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YA AACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEABFViEkUC AABRBAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAxyBi vuAAAAAJAQAADwAAAAAAAAAAAAAAAACfBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAA AKwFAAAAAA== " strokecolor="white [3212]">

(3.6)

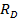С другой стороны, укорочение бруса от действия реакции равно: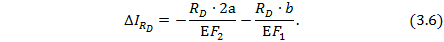

(3.7)

Из условия совместности деформаций (отсутствие перемещение в т. D)

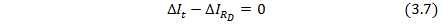
имеем равенство:

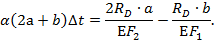
Тогда неизвестная реакция 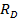из полученного равенства будет:

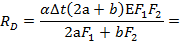
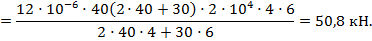
Напряжения в поперечных сечениях в средней части стержня:

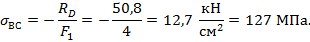
Напряжение в поперечных сечениях крайних частей стержня:

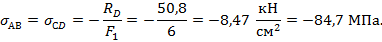
Знаки «минус» в напряжениях соответствуют тому, что напряжения сжимающие.