Геометрическая интерпретация диф.ур.1 порядка.

Пусть дано диф. уравнение (4), разрешенное относительно производной

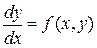(6)

, и пусть (5) есть общее решение данного уравнения. Это общее решение определяет семейство интегральных кривых на плоскости OXY.

Уравнение (6) для каждой точки M с координатами х и у определяет значение производной 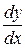, т.е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Диф. Ур. (6) определяет поле направлений на плоскости Оху.

Следовательно, с геометрической точки зрения задача интегрирования диф.ур. заключается в нахождении кривых, направление касательных которых совпадает с направлением поля в соотвествующих точках.

Для диф ур (2) геометрическое место точек, в которых выполняется соотношение 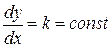, называется изоклиной.

При различных значениях k получаем различные изоклины. Построив семейство изоклин можно приближенно построить семейство интегральных кривых.

Задача Коши для дифференциального уравнения первого порядка имеет вид:

;

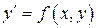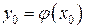- начальное условие.

Теорема (Теорема существования и единственности решения задачи Коши). Если в уравнении (1.3) функция 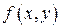и ее частная производная 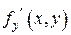непрерывны в некоторой области 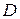, содержащей точку 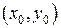, то существует единственное решение 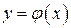этого уравнения, удовлетворяющее начальному условию .

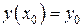Уравнения 1-го порядка и методы их решений:

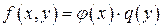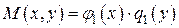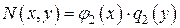1.Уравнения с разделяющими переменными. Это уравнения вида (4), у которых , или вида (3), у которых и , где .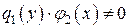

Решение. Уравнение (3) сводится к виду 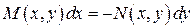. Получим 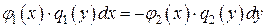. Делим обе части на 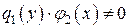и интегрируем: 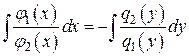или 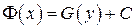– общий интеграл данного уравнения.

Деление на 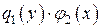может привести к потере частных решений, являющихся корнями уравнения 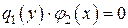. Наличие особых решений устанавливаем проверкой.

Пример 1. Решить уравнение 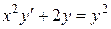при начальных условиях .

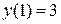Это уравнение является уравнением с разделяющимися переменными. Перенеся 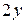в правую часть уравнения и учитывая, что 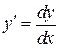, запишем:

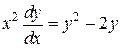или .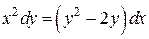

Разделив обе части последнего уравнения на 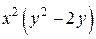, получим уравнение 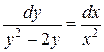, которое уже является уравнением с разделенными переменными.

Проинтегрируем обе части уравнения .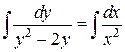

Интеграл 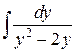можно представить в виде

.

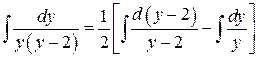Получим .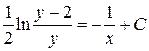

Последнее выражение, записанное в виде 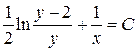, называется общим интегралом соответствующего дифференциального уравнения.

Для нахождения частного решения подставим в общий интеграл значения 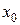, , 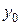то есть 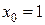, 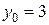: 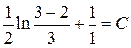, откуда следует, что .

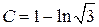Значит, 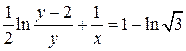или .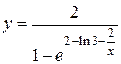

Ответ: .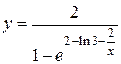

2. Однородные дифференциальные уравнения. Это уравнения вида 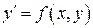, в которых правую часть можно привести к виду 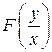. Тогда

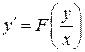. (1.7)

Для решения полагаем 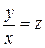, где 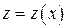. Имеем 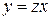; 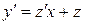. Подставив это выражение в (1.7), получим 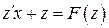или 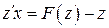, т.е. уравнение с разделяющимися переменными. После решения заменим .

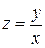Пример 3. Решить уравнение .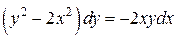

Это уравнение является однородным дифференциальным уравнением, т.к. в преобразованном виде 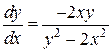правая часть является однородной функцией нулевого порядка.

Уравнение 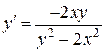решаем заменой 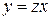, где 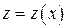. Тогда 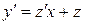. Подставив выражения для 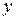и 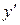в исходное уравнение, получим 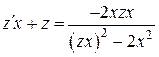или 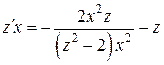. Последнее выражение приведем к виду 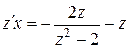, т.е. 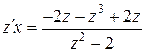. Это уравнение с разделяющимися переменными.

Заменяя 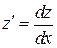и упрощая правую часть последнего равенства, будем иметь 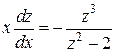, , 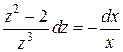, 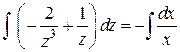откуда .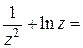

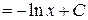Окончательно, заменяя 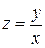, получим общий интеграл исходного уравнения: 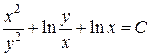или .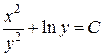

2. Линейные неоднородные уравнения. (Линейные дифференциальные уравнения первого порядка). Это уравнения вида

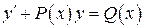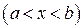, , (1.5)

где 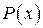, 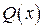– непрерывные функции на .

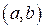Решение. Решение ищется методом Бернулли, с помощью подстановки 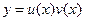, где 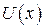– новая неизвестная функция; 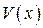– некоторая функция, значение которой определяется так:

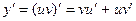; Тогда получаем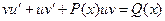

или 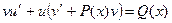. (1.6)

Выберем 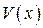так, чтобы выражение в скобках обратилось в нуль:

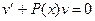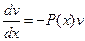, . (1.7)

Решение, полученного для функции 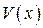, дифференциального уравнения с разделяющимися переменными:

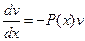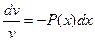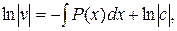, , В виду свободы выбора функции 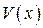, можно принять 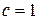. Отсюда

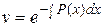(1.8)

(1.8) подставим в (1.6). 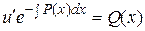В результате получим для неизвестной функции 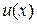уравнение с разделяющимися переменными.

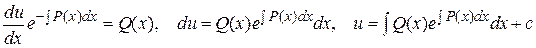
Его решение позволяет найти исходную неизвестную функцию .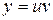

Пример 4. Решить уравнение .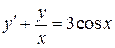

Это уравнение является линейным неоднородным дифференциальным уравнением (ЛНДУ).

Решим его методом Бернулли. Будем считать, что 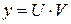, тогда 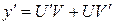; эти выражения подставим в исходное уравнение

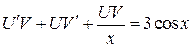или .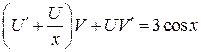

Выберем 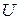так, чтобы 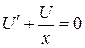или 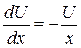, откуда 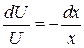. Проинтегрировав обе части последнего уравнения, будем иметь 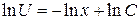. Возьмем 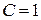, так что 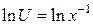, значит .

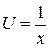Выражение 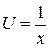подставим в уравнение 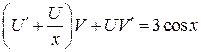, получим 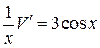или 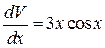, откуда 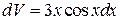, 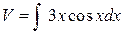. Интегрируя по частям, найдем : .

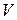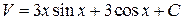В силу того, что 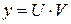, получим 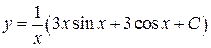и окончательно будем иметь общее решение .

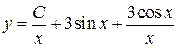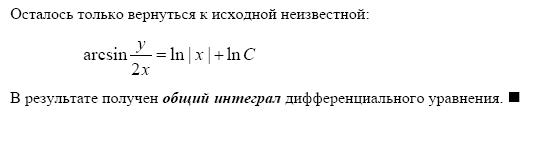
Уравнения Бернулли.

Уравнения вида 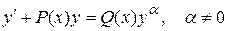называются уравнениями Бернулли.

Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка z=y^-n+1 сводит уравнение (2.15) к линейному. На практике ДУ (2.15) удобнее искать методом И. Бернулли в виде y=u•v (не сводя его к линейному).

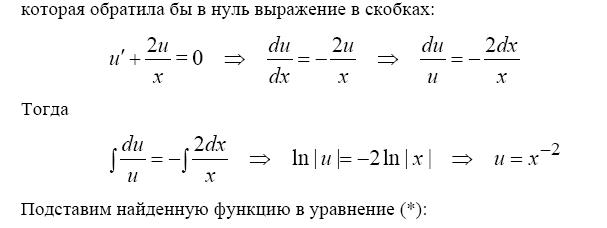
Дифференциальные уравнения первого порядка. Методы решения.

1. Обыкновенные диф.ур. 1-го порядка

2. Уравнение, разрешенное относительно производной.

3. Общее решение и частное решение.

4. Геометрическая интерпретация диф.ур.

5. Задача Коши для диф.ур.

6. Теорема существования и единственности решения задачи Коши.

7. Уравнения с разделяющимися переменными.

8. Пример 1. Решить уравнение 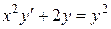при начальных условиях .

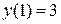9. Пример 2. Решить уравнение 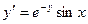с начальным условием .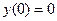

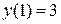10. Однородные диф.уравнения.

11. Пример 3. Решить уравнение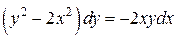

12. Линейные неоднородные уравнения.

13. Пример 4. Решить уравнение .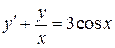

14. Пример 4. Решить уравнение .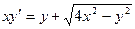

15. Уравнения Бернулли

16. Пример 2. Решить уравнение 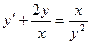с начальным условием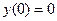 .
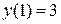