Базисные решения. Базисные допустимые решения (БДР)

Пусть задана задача ЛП (2.1.1) в стандартной форме. Предположим, что матрица 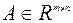, 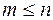имеет ранг 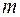, т.е. имеет 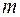линейно – независимых столбцов. Обозначим 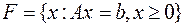- допустимое множество.

Базисом матрицы 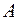называется набор 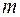линейно независимых столбцов .

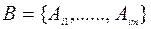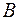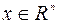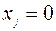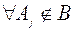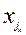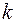Базисным решением, соответствующим базису , называется вектор , для которого , , есть -я компонента вектора , .

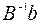Базисные решения ограничений могут быть получены, если приравнять нулю 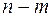переменных и решить 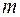уравнений относительно оставшихся 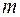переменных. Предполагается, что эти уравнения имеют единственное решение.

Если базисное решение 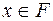, то 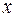называется базисным допустимым решением.

Отрезок 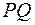определяется соотношением

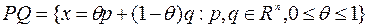
Множество 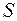называется выпуклым, если для любых точек 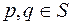отрезок 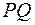содержится в .

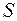Вершиной или углом выпуклого множества называется любая точка, не лежащая внутри произвольного отрезка, соединяющего разные точки множества.

Выпуклой оболочкой точек 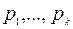называется множество точек вида

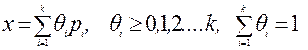
Теорема 1. Допустимая область задачи (2.1.1) является выпуклым множеством.

Теорема 2.Базисные допустимые решения задачи (2.1.1) соответствуют вершинам допустимого выпуклого множества .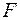

Теорема 3.Если множество 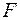непусто и матрица 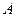имеет ранг 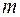, то в задаче (2.1.1) существует, по крайней мере, одно БДР.

Теорема 4.Если в задаче (2.1.1) имеется конечный минимум , то по крайней мере одно оптимальное решение является БДР.

Пример.Задача (2.0.1) может быть приведена к следующему виду

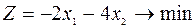
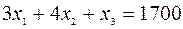(2.0.1.а)

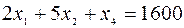
В матричной форме ограничения задачи имеют вид

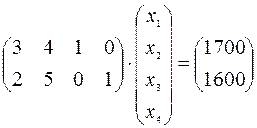
Все возможные базисные решения могут быть сведены в таблицу

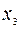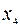				-525
					A
	566	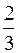		466	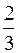C
			-700
					B

Допустимые базисные решения изображены на рис. 1.