Базисные векторы и годографы

Вернёмся к нашим параметрическим кривым. Изобразим теперь на рисунках радиус-векторы

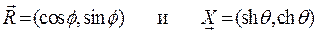
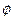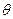и их производные по параметрам и («скорости»)

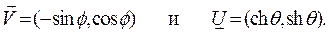
Векторы и 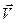являются единичными (в обычном евклидовом смысле), причём 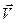повёрнут относительно на ¼ оборота против часовой стрелки. Векторы и 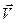ортогональны (т.е. 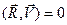). Векторы 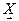и 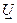также являются единичными (в смысле метрики Минковского 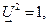а 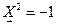), причём 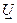связан с 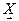отражением относительно прямой 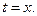Векторы 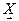и 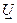ортогональны (т.е. ).

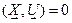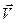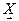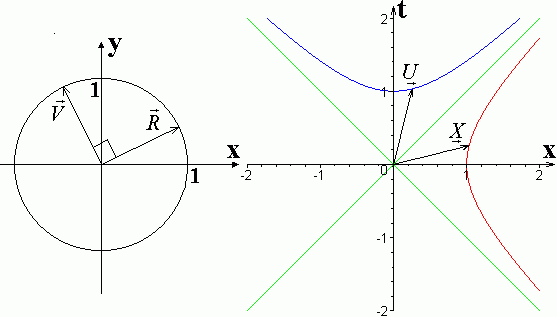
Таким образом, по мере того, как конец вектора движется по единичной окружности, конец вектора движется по той же окружности с опережением на ¼ оборота (т.е. годограф совпадает с самой единичной окружностью). По мере того как конец вектора движется по одной (красной) гиперболе снизу вверх, конец вектора симметрично движется по другой (синей) гиперболе слева направо. Уравнение годографа (синей гиперболы)

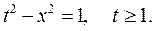
Поворот

Если взять векторы и в качестве базисных векторов новой системы координат, то новая система координат будет повёрнута относительно системы 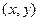на угол 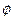. Обратная матрица поворота оказывается составлена из компонент единичных векторов и

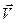
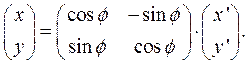
Если мы возьмём 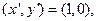то получим, что первый столбец матрицы образован компонентами вектора , если мы возьмём 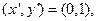то получим, что второй столбец матрицы образован компонентами вектора .

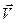В повёрнутой системе координат формула для длины по прежнему справедлива (только со штрихами над координатами), это следует из того, что скалярные произведения базисных векторов такие же как и в исходной системе ( 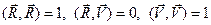). Поэтому все окружности с центром в начале координат после поворота задаются теми же уравнениями.

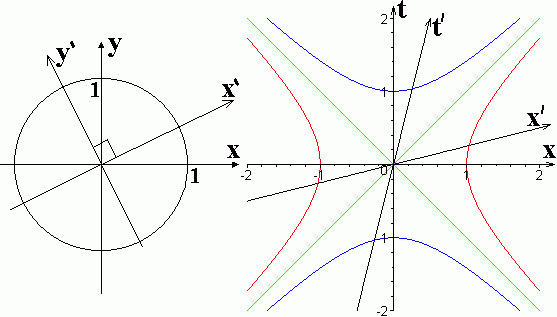
На рисунках изображены системы координат связанные друг с другом преобразованиями поворота и буста. Изображённые на рисунках единичная окружность и псевдо-окружности (гиперболы) отсекают на осях координат плюс-минус единичные точки. Наклон оси 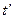задаётся значением скорости (вдоль оси ).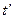

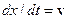Буст

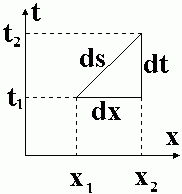Если взять векторы 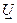и 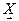в качестве базисных векторов новой системы координат, то новая система координат будет связана с системой 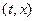преобразованием Лоренца (бустом), аналог угла — 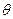называется быстротой.

Обратная матрица буста составлена из компонент единичных векторов 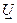и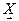

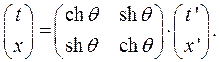
Если мы возьмём 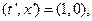то получим, что первый столбец матрицы образован компонентами вектора 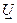, если мы возьмём 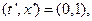то получим, что второй столбец матрицы образован компонентами вектора .

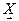Как определить, какой скорости соответствует это преобразование? Скорость системы отсчёта — это скорость точки, которая во все моменты времени имеет в этой (движущейся) системе отсчёта нулевые пространственные координаты. Т.е. траектория этой точки в пространстве-времени (мировая линия) — ось времени движущейся системы отсчёта. Дифференцируя вдоль направления новой оси времени (вдоль вектора 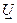) 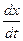получаем скорость

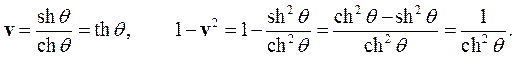
Отсюда легко найти, что

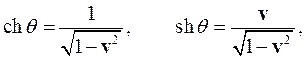
и записать преобразование Лоренца в более привычном виде

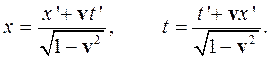
Напомним, что наличие времени в законе преобразования для координаты нет ничего нового по сравнению с классической механикой: как и в классике наклон оси времени (мировой линии начала координат) соответствует скорости. Присутствие координаты в законе преобразования времени интереснее, т.к. оно означает изменение наклона оси 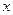, а ось 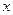— множество событий одновременных с событием в начале координат. «Относительность одновременности» — это наклон оси .

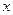В системе координат после буста 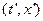формула для интервала по прежнему справедлива (только со штрихами над координатами), это следует из того, что скалярные произведения базисных векторов такие же как и в исходной системе ( 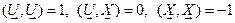). Поэтому все псевдо-окружности (гиперболы) с центром в начале координат после поворота задаются теми же уравнениями.

Круговой угол

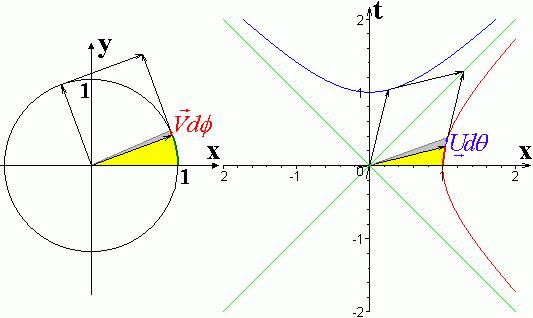
См. рисунок в конце раздела.

Величина угла 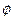может быть геометрически интерпретирована как удвоенная площадь сектора между осью 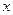, радиус-вектором и дугой окружности (жёлтый сектор на рисунке) или длина дуги окружности, ограничивающей этот сектор (выделена зелёным). Хотя эти факты и очевидны, докажем их (чтобы потом можно было сравнить это доказательство, с аналогичным доказательством в гиперболическом случае).

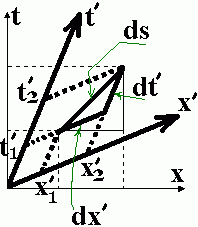
Рассмотрим бесконечномалое приращение 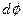аргумента 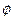. Вектор при этом получит приращение 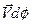(маленький красный вектор). Площадь выделенного сектора возрастёт на площадь бесконечномалого треугольника (нарисован серым цветом). Приращение площади сектора равно половине векторного произведения векторов и 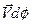(определителя составленного из компонент этих векторов).

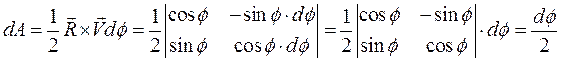
Т.е. получился определитель обратной матрицы поворота умноженный на 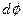. Определитель матрицы поворота равен 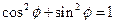(площадь квадрата натянутого на векторы и 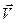), это связано с тем, что поворот сохраняет площадь.

Приращение длины дуги равно 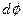умноженному на длину вектора 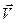(т.е. на 1).

Таким образом, оба определения угла (через площадь сектора и через длину дуги) доказаны, причём доказательства показали связь этих свойств со свойствами поворота сохранять площадь и длину.

Гиперболический угол (быстрота)

Проделаем теперь аналогичные выкладки в гиперболическом случае.

Величина угла 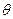может быть геометрически интерпретирована как удвоенная площадь сектора между осью 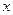, радиус-вектором и дугой гиперболы (жёлтый сектор на рисунке) или интервал вдоль дуги гиперболы, ограничивающей этот сектор (выделена толстой красной линией). Эти факты уже не столь привычны, как в круговом случае.

Рассмотрим бесконечномалое приращение 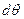аргумента 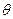. Вектор 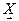при этом получит приращение 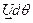(маленький синий вектор). Площадь выделенного сектора возрастёт на площадь бесконечномалого треугольника (нарисован серым цветом). Приращение площади сектора равно половине векторного произведения векторов 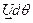и 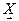(определителя составленного из компонент этих векторов).

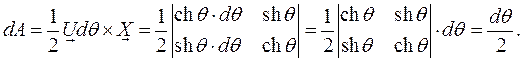
Т.е. получился определитель обратной матрицы буста умноженный на 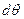. Определитель матрицы, буста равен 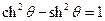(площадь ромба натянутого на векторы 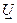и 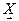), это связано с тем, что буст сохраняет площадь.

Приращение интервала вдоль дуги равно 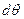умноженному на интервал вдоль вектора 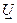(т.е. на 1).

Таким образом, оба определения гиперболического угла (через площадь сектора и через интервал вдоль дуги) доказаны, причём доказательства показали связь этих свойств со свойствами буста сохранять площадь и интервал.