Изучение распределения магнитного поля

Внутри соленоида

1 Магнитное поле соленоида

2 Закон Био–Савара–Лапласа

3 Эффект Холла

Основные понятия по теме

Соленоидом называется длинная катушка с большим числом витков в обмотке. На рисунке 4.1 показана катушка в разрезе плоскости чертежа. Ток в верхних сечениях витков катушки направлен к читателю, а в нижних – от читателя.

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

S

N

Рисунок 4.1 – Катушка соленоида в разрезе

Магнитная стрелка, помещённая внутри катушки, показывает своим северным полюсом направление магнитного поля внутри катушки. Полярность магнитного поля определяется по правилу правой руки: если ладонь правой руки наложить на витки катушки так, чтобы четыре пальца указывали направление тока в витках катушки, то отставленный на 90° (по отношению к указательному) большой палец укажет северный магнитный полюс катушки. В центре соленоида магнитные поля складываются, и возникает почти однородное поле.

Соленоид, витки которого расположены вплотную друг к другу, эквивалентен системе круговых токов, одинаковых по радиусу и имеющих общую ось. На основании закона Био–Савара–Лапласа и принципа суперпозиции индукция магнитного поля на оси кругового тока i радиуса r равна:

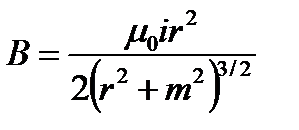, (4.1)

где m – расстояние от центра кругового тока до точки, в которой определяется индукция.

Для нахождения индукции магнитного поля всего соленоида его делят на такие элементы, каждый из которых можно считать круговым витком, а затем применяют принцип суперпозиции. Такой элемент толщины 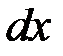показан на рисунке 4.2 и содержит 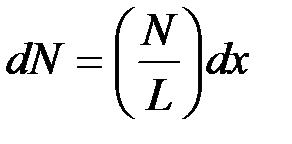витков. Сила тока в нём:

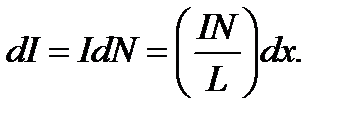(4.2)

В соответствии с формулами (4.1) и (4.2) индукция магнитного поля, созданного таким элементом, равна:

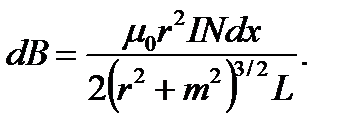(4.3)

Поскольку все элементарные векторы 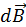коллинеарные, индукция результирующего поля находится интегрированием выражения (4.3) по всей длине соленоида. Магнитная индукция зависит от диаметра соленоида D = 2r, его длины L и расстояния X_C. Как будет показано ниже, в центре соленоида магнитная индукция для бесконечно длинного соленоида определяется по приближённой формуле

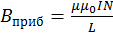, (4.4)

где 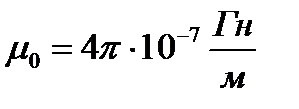– магнитная постоянная вакуума, 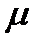– относительная магнитная проницаемость сердечника соленоида (для неферромагнитных материалов, таких как воздух, дерево, медь, алюминий 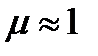), I – ток соленоида, N – количество витков соленоида, L – длина соленоида.

Найдём индукцию магнитного поля соленоида в точке С, лежащей на оси соленоида на расстоянии 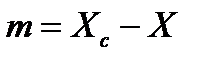от его середины.

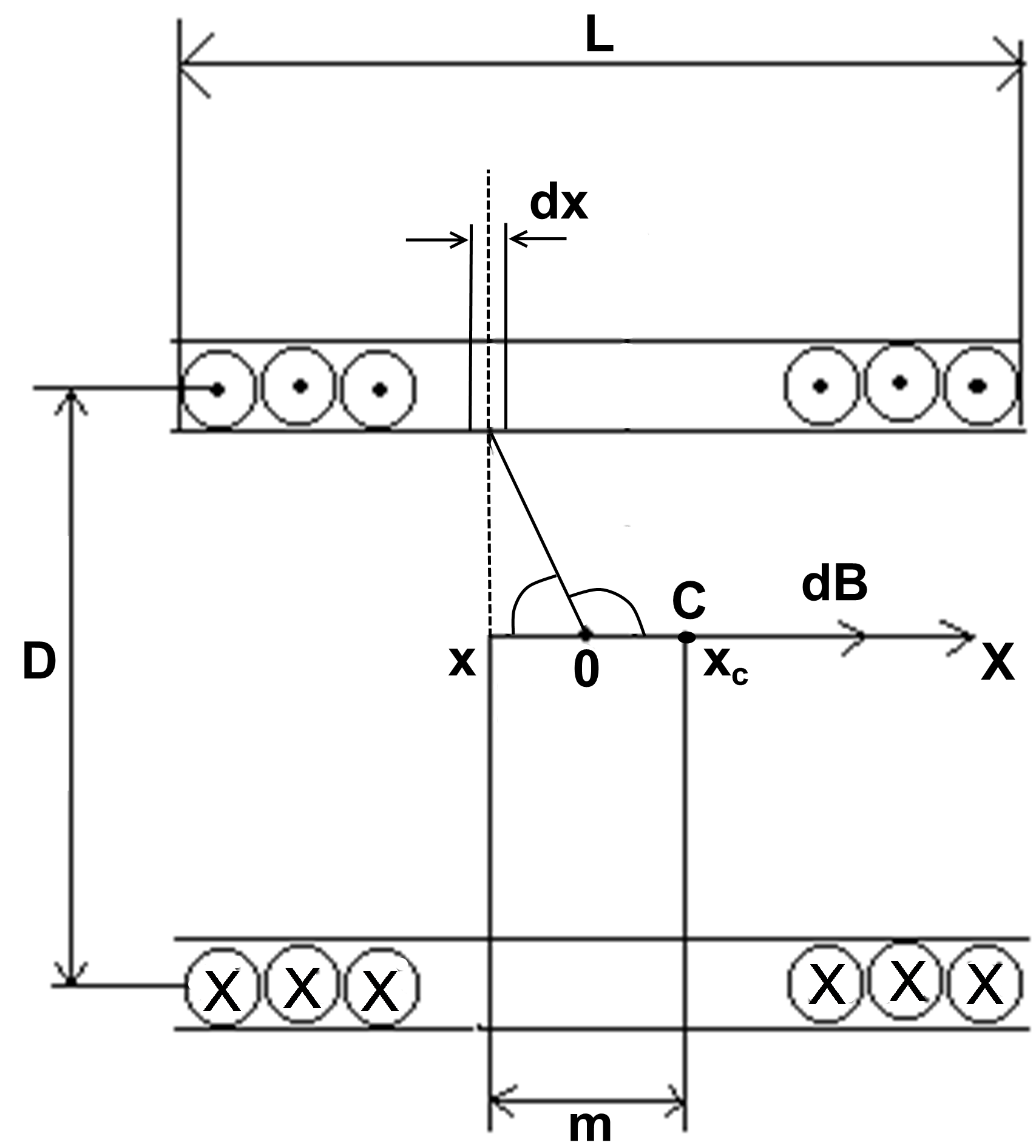
Для проведения расчёта введём координатную ось ОХ. Начало координат поместим в середину соленоида (рисунок 4.2), тогда X_C – координата точки С. Произвольный элементарный виток толщины dxс координатой Х находится от точки С на расстоянии .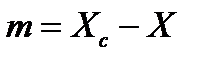

Подставим это выражение в формулу (4.3):

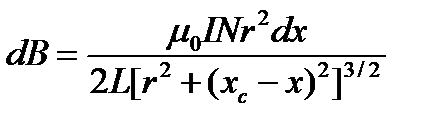. (4.5)

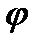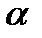Рисунок 4.2 – Элемент расчета индукции соленоида

При суммировании индукции полей, созданных всеми элементами, координата Х изменится от – 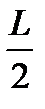до + .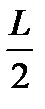

Для упрощения интегрирования введём в качестве переменной интегрирования угол 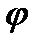, умножив предварительно числитель и знаменатель выражения (4.5) на r. При подстановке учтём, что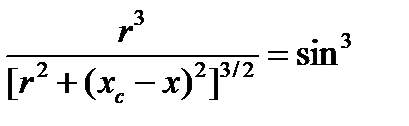

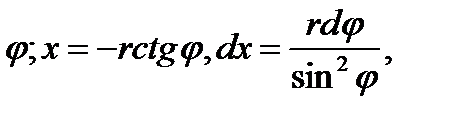
тогда выражение (4.5) примет вид:

.

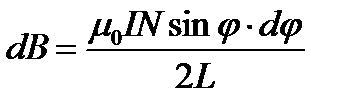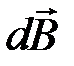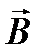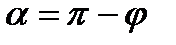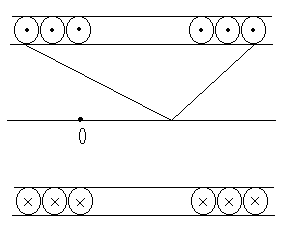
Поскольку на рисунке 4.2 вектор , а значит и вектор направлен по оси ОХ, введём окончательно в качестве переменной интегрирования угол , тогда 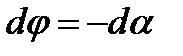, причём угол изменяется для точки С от 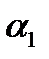до 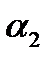(рисунок 4.3).

C

α1

α2

Рисунок 4.3 – Элемент расчета индукции соленоида

Окончательно получаем: ,

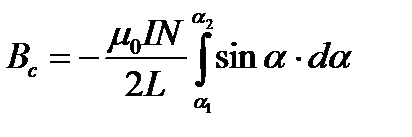
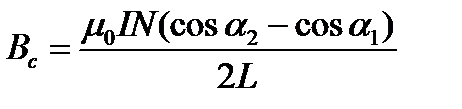. (4.6)

Как видно:

, .

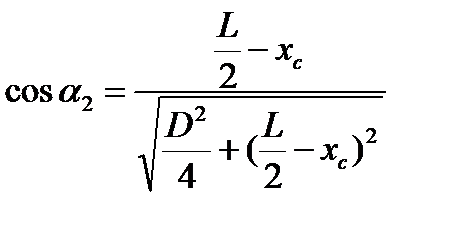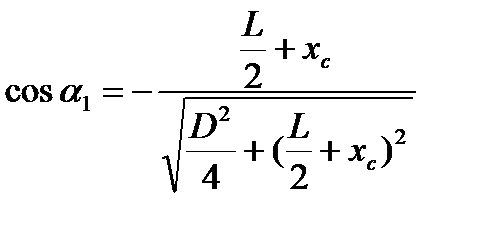В середине соленоида 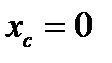, 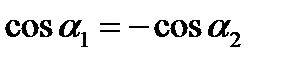и выражение (4.6.) принимает вид

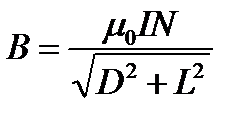. (4.7)

Если длина соленоида значительно превышает его диаметр (D << L), то из формулы (4.7) следует приближённое выражение (4.4) для магнитной индукции на оси бесконечно длинного соленоида.

При использовании формулы (4.4) относительная погрешность равна:

.

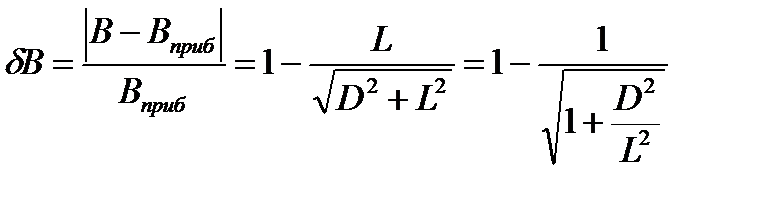Разложив 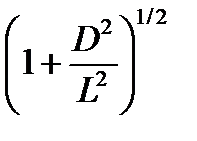в степенной ряд по переменной 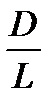и, отбрасывая члены, содержащие 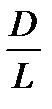в степени больше двух, получим:

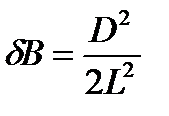. (4.8)

Задавая относительную погрешность измерения магнитной индукции 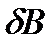, можно найти соотношение между длиной и диаметром соленоида:

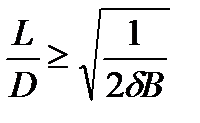. (4.9)

Принимая поле внутри катушки однородным, а линии магнитного поля параллельными её оси, находим магнитный поток Φ внутри катушки:

,

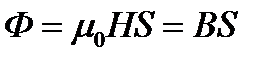где Н –напряжённость поля, .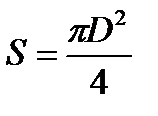

Итак, используя формулы (4.4), (4.6), (4.7), можно определить магнитную индукцию поля в зависимости от координаты вдоль оси соленоида расчётным путём. В данной работе для определения магнитной индукции поля внутри соленоида опытным путём используется датчик Холла, работа которого основана на эффекте Холла.

Эффектом Холла называется явление возникновения Э.Д.С. между боковыми гранями пластинки с током, помещённой в поперечное магнитное поле.

Эффект Холла объясняется действием силы Лоренца на движущиеся в пластине заряженные частицы. Величина этой силы определяется формулой:

,

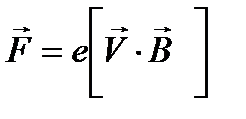где e – заряд частицы, 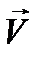– скорость ее движения; 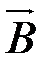– вектор магнитной индукции поля, квадратные скобки означают векторное произведение.

Если к граням 1 и 2 полупроводника, имеющего форму пластины, приложить постоянное напряжение (рисунок 4.4), то в цепи возникает ток.

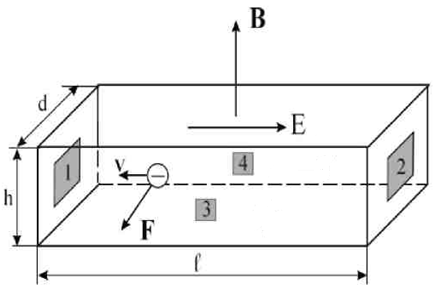
Рисунок 4.4 – Датчик Холла (полупроводник n-типа)

При этом движущиеся носители зарядов полупроводника под действием силы Лоренца будут отклоняться в перпендикулярном направлении, и между точками 3 и 4 возникнет разность потенциалов,ε_x, называемая Э.Д.С. Холла.

Действие силы Лоренца можно рассматривать как действие эффективной электростатической силы с напряжённостью

.

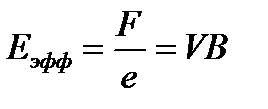Тогда разность потенциалов, возникающая между точками 3 и 4, равна ε_х = VBd,

где d – расстояние между поверхностями 3 и 4.

Введём в рассмотрение плотность тока

,

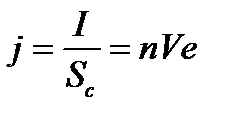где n – концентрация носителей заряда, S_c = dh – площадь грани 1 (или 2), h – толщина пластинки. Теперь Э.Д.С. Холла можно записать в виде

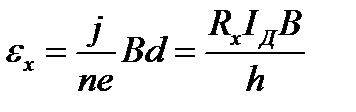, (4.10)

где 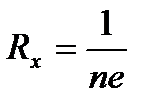– постоянная Холла, I_Д= 0,09А – рабочий ток датчика.

Из уравнения (4.10) следует, что если I = const, то ε_х = f(B).

Основными параметрами преобразователя Холла являются следующие параметры:

– номинальное значение управляющего тока I_макс (рабочий ток);

– входное сопротивление R₁₀. Измеряется между управляющими электродами преобразователя Холла. При В = 0 значение R₁₀ указывается в паспорте;

– выходное сопротивление R₂₀. В паспорте указывается значение R₂₀ между холловскими электродами при разомкнутой цепи и отсутствии магнитного потока;

– чувствительность к магнитной индукции определяется выражением

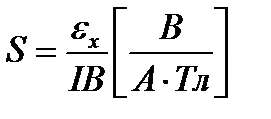. (4.11)

Вопросы для самоконтроля

1 Поясните зависимость магнитной индукции от координаты вдоль оси соленоида. Приведите расчётные формулы.

2 Как определить полярность магнитного поля соленоида?

3 Сформулируйте закон Био–Савара–Лапласа.

4 Объясните сущность метода измерения индукции магнитного поля при помощи датчика Холла.

5 Приведите примеры практического применения явления Холла.

Лабораторная работа 4