Двухфакторный дисперсионный анализ

Цель работы: познакомиться с процедурой двухфакторного дисперсионного анализа.

Процедура двухфакторного дисперсионного анализа

Двухфакторный дисперсионный анализ обобщает случай однофакторного анализа. Пусть имеется два фактора – А и В. Для фактора А выделим р уровней, для фактора В – q уровней. Всего, таким образом, имеем рq возможных уровневых состояний, или ячеек. Для каждой рq ячейки проводится n наблюдений, значит общее число наблюдений N = npq.

При проведении двухфакторного дисперсионного анализа также используются результаты объемной группировки и таблица совместимости, но вместо количества попаданий в этой таблице проставляются значения третьего фактора. Рассматриваются те факторы, у которых при проведении объемной группировки не было нулевых значений в ячейках.

Рассмотрим сначала зависимость извлечения от выхода концентрата и содержания металла в сульфате (табл. 6.1). Совместимость со значениями результатов извлечения, полученная в результате объемной группировки представлена в табл. 6.2.

Таблица 6.1

	Содержание металла в сульфате
Выход концентрата	0,40 – 0,65	74,8	66,83	71,57
	74,57	72,57	71,03
	74,33	74,47	66,63
		71,67	72,57
		72,9
		72,6
		74,65
0,65 – 0,90	75,6	76,45
	76,73	73,4
	75,17	74,83
	77,37	72,73
	75,67
0,90 – 1,15	76,87	67,7	71,67
	78,1	70,85	80,6

Таблица 6.2

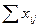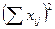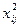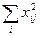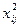223,7	505,69	281,8	1011,19	1022505,216	50041,69	255722,38	79411,24	385175,31	5595,04	4466,25	5122,26
223,7	297,41		593,11	351779,4721	50041,69	88452,708		143678,4	5560,68	5266,40	5045,26
154,97	138,55	152,27	445,79	198728,7241	24015,701	19196,103	23186,153	66397,956	5524,95	5545,78	4439,56
										5136,59	5266,40
										5314,41
										5270,76
										5572,62
									5715,36	5844,60	5184,00
									5887,49	5387,56
									5650,53	5599,53
									5986,12	5289,65
									5725,95
									5909,00	4583,29	5136,59
									6099,61	5019,72	6496,36
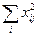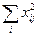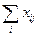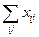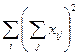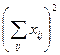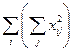16680,57	36572,82	19873,49	73126,98	602,37	2050,09	1573013,4		595251,66	162642,3377	362849,62
28965,45	22121,34	5184,00	56270,79	941,65						886704,7225
12008,61	9603,01		33244,57	506,07						256106,8449
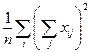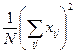1505661,18		157301,34	178575,5	140095,63

После проведения необходимых расчетов результаты сводятся в таблицу:

Показатели	Сумма квадратов	Степень свободы	Средние квадраты	Fр	Fт	%
Фактор А (выход концентрата)	–17205,71		–8602,85	11,34	3,47	–6%
Фактор В (содержание металла в сульфате)	–17205,71		–8602,85	11,34	3,47	–6%
Фактор А×В (извлечение)	318671,13		79667,78	–105,00	2,84	119%
Внутри ячеек	–15933,16		–758,72
Сумма	268326,56

Из-за нехватки наблюдений сумма некоторых квадратов оказалась отрицательным числом. В силу этого полученные в ходе дисперсионного анализа данные невозможно далее проанализировать.

Рассмотрим теперь влияние выхода концентрата и содержания металла в сульфате на содержание металла в руде.

Совместимость со значениями содержания металла в руде, полученная в результате объемной группировки, приведена в табл. 6.3.

Таблица 6.3

	Содержание металла в сульфате
Выход концентрата		0,28 – 0,54	0,54 – 0,81	0,81 – 1,07
0,40 – 0,65	0,47	0,62	0,58
	0,51	0,49	0,49
	0,6	0,47	0,5
		0,45	0,57
		0,52
		0,56
		0,52
0,65 – 0,90	0,59	0,7	0,57
	0,59	0,61
	0,55	0,62
	0,67	0,66
	0,56
0,90 – 1,15	0,96	0,52	0,52
	0,73	0,62	0,61

После проведения необходимых расчетов результаты сводятся в таблицу, приведенную ниже:

Показатели	Сумма квадратов	Степень свободы	Средние квадраты	Fр	Fт	%
Фактор А (выход концентрата)	–1		–0,31521	44,197169	3,4667949	–46%
Фактор В (содержание металла в сульфате)	–0,63042		–0,31521	44,197169	3,4667949	–4%
Фактор А×В (содержание металла в руде)			4,787805	–671,322006	2,8400962	108%
Внутри ячеек	–0,15		–671,2206
Сумма

Как и в первом случае, полученные в ходе дисперсионного анализа результаты нельзя проанализировать далее, так как сумма квадратов не может быть отрицательным числом (это произошло из-за нехватки наблюдений).

Порядок выполнения работы

1. Изучить процедуру проведения двухфакторного дисперсионного анализа используя приведенные методики и данные табл. 1 приложения.

2. На основе объемной группировки построить таблицы совместимости двух факторов, опираясь на материалы лабораторной рабо-
ты 5 и [2].

3. В таблице совместимости проставить значения третьего фактора по выбранному варианту.

4. Рассчитать критерии Фишера, сравнить с табличными значениями, используя материалы лекций.

Контрольные вопросы

1. В чем отличие двухфакторного дисперсионного анализа от однофакторного?

2. Может ли критерий Фишера быть меньше 1?

3. Как определить, существенно ли различие между средними двух частных совокупностей?

4. Как построить таблицу совместности для двухфакторного дисперсионного анализа?

5. Чем корреляционно-регрессионный анализ по сути отличается от дисперсионного анализа?

Лабораторная работа 7