Синтез АСР температуры с непрерывным регулятором
Основное назначение регулятора в АСР – получение заданных динамических и статических характеристик ОР. Основными требованиями, предъявляемыми к системе регулирования температуры, являются: максимальное быстродействие и нулевая статическая ошибка.
Структура АСР включает интегрирующее звено – исполнительный механизм, что уже обеспечивает нулевую статическую ошибку. Наличие запаздывания же снижает запас устойчивости.
Выполним расчет непрерывного регулятора, который обеспечит максимально возможное быстродействие системы, отсутствие колебательности и достаточный запас устойчивости.
При расчетах регуляторов решается одна из основных задач: формирование желаемых логарифмических амплитудно- и фазо-частотных характеристик.
На рис. 4.6 приведена амплитудно-частотная и фазо-частотная логарифмические характеристики объекта регулирования.
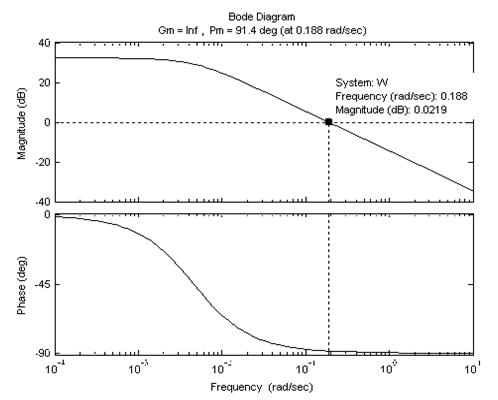
Рис. 4.6. Логарифмические частотные характеристики объекта регулирования
Запас устойчивости по фазе равен 91,4 град.
Считаем, что максимальная частота пропускания объектом соответствует частоте среза 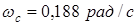 . Период сигнала равен
. Период сигнала равен 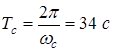 .
.
В соответствии с теоремой Котельникова для представления сигнала в цифровом виде период дискретизации должен быть в два раза меньше периода сигнала. Примем период дискретизации в пять раз меньше 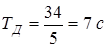 .
.
Рассчитаем непрерывный регулятор для линейной системы. Для нашей системы применим ПД-регулятор. В сравнении с П-регулятором, использование ПД-регулятора позволяет повысить запасы устойчивости системы и улучшить качество регулирования.
Общий вид передаточной функции ПД-регулятора
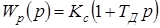 ,
,
где Кс – коэффициент передачи пропорциональной части регулятора,
ТД – постоянная времени дифференциальной составляющей регулятора. На практике реализовать идеальное дифференцирование невозможно, так как частотная характеристика звена бесконечно увеличивается на высоких частотах. Поэтому используют дифференцирующее звено с дополнительным фильтром
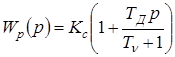 ,
,
где Тn – постоянная времени фильтра, которая обычно в 3-10 раз меньше, чем ТД. Чрезмерное увеличение ТД может привести к неустойчивости системы, уменьшение этой величины затягивает переходной процесс.
Для расчета регулятора используем инструмент sisotool пакета MATLAB, который позволяет синтезировать регулятор по корневому годографу на основе частотных характеристик.
Желаемую ЛАЧХ строим таким образом, чтобы ее наклон в среднечастотной области был не ниже 20 дБ на декаду, что обеспечивает монотонный переходный процесс.
В рабочем окне MATLAB задаем передаточные функции ОР и предполагаемого регулятора, после чего вызываем команду sisotool. Диалоговое окно Open-Loop Bode Editor позволяет корректировать желаемую ЛАЧХ разомкнутого контура (рис. 4.7). Выбираем настроечные параметры регулятора: Кс = 0,1, ТД = 12.
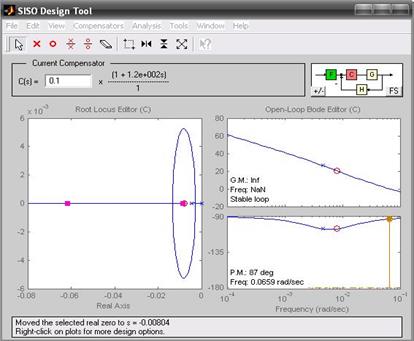
Рис. 4.7. Диалоговое окно Open-Loop Bode Editor
Для проверки работоспособности системы с выбранным ПД-регулятором соберем модель АСР (рис. 4.8) и построим переходную характеристику. Анализ характеристики свидетельствует о том, что система устойчива, время регулирования не превышает заданного, следовательно, регулятор выбран и рассчитан правильно.
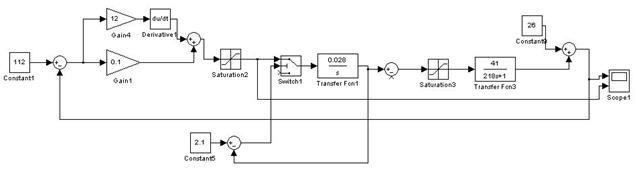
Рис. 4.8. Схема моделирования АСР с непрерывным ПД-регулятором
