Некоторые типовые примеры с решениями

Раздел 1.

Пример 1.1. Решить систему линейных уравнений, пользуясь формулами Крамера.

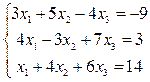
Определитель данной системы

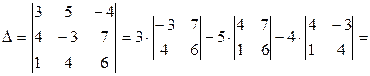
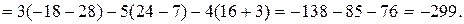
Вычислим определитель 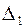, 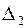и :

.

.

.

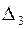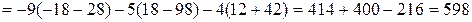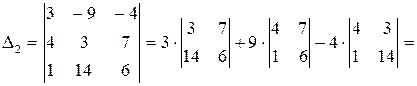
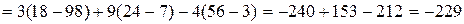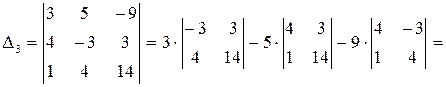
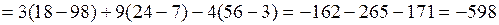Решение системы: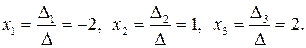

Для того чтобы убедиться в правильности решения, подставим эти значения 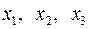в исходную систему

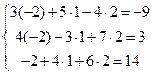
Раздел 2.

Пример 2.1. Найти угол φ между векторам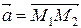и и 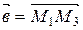, если М₁(1, -2, -3), М₂(-3, 1, 1), М₃(3, 2, 2).

Решение. Для нахождения cosφ используем формулу

,

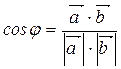где 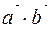- скалярное произведение векторов 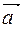и .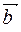

Определим координаты векторов 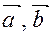и cosφ:

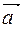= {-3-1, 1+2, 1+3} ={-4, 3, 4}, 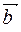= {3-1, 2+2, 2+3} = {2, 4, 5},

,

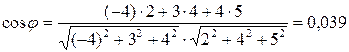φ = 87⁰45'54^».

Пример 2.2. Даны координаты вершин пирамиды А₁(1, -2, -3), А₂(-3, 1, 1), А₃(4, 3, -1), А₄(3, 2, 2). Найти площадь грани А₁ А₂ А₃ и объем пирамиды.

Решение.

1. Площадь треугольника А₁А₂А₃ найдем, используя геометрический смысл векторного произведения векторов

,

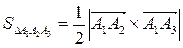где 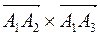- векторное произведение векторов.

, .

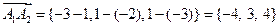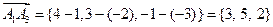Вначале находим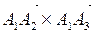

,

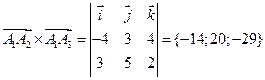а затем

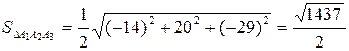ед².

2.Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов

,

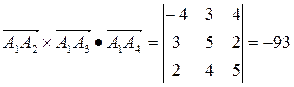следовательно, 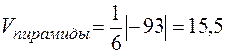ед³.

Раздел 3.

Пример 3.1. Найти расстояние между точками М₁(1, -2, -3) и М₂(-3, 1, 1). Определить координаты точки С, делящей отрезок М₁М₂ в отношении 2:3.

Решение.

Используя формулу

М₁М₂ = ,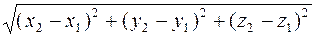

получим М₁М₂ = .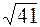

Координаты точки С определим по формуле вида

,

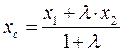где .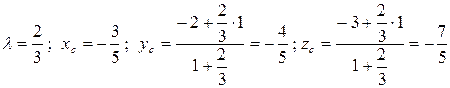

Пример 3.2. Даны вершины треугольника А(-3,-3), В(2,7) и С(5,1). Требуется написать уравнения сторон треугольника, определить угол А треугольника, найти уравнение медианы АК и высоты АМ.

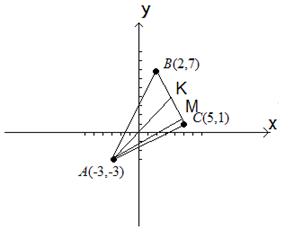
Рис. 1.

Решение. Чтобы написать уравнение стороны АВ треугольника, используем вид уравнения прямой, проходящей через две точки:

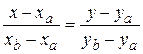
AВ: 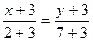или у = 2х + 3.

Аналогично

АС: 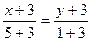или у = 0,5х -1,5

СВ: 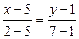или у = -2х +11.

Тогда тангенс угла А определяется по формуле:

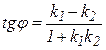, k₁=2, k₂ = 0,5. Следовательно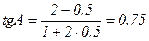

Ищем уравнение медианы АК. Для этого определяем координаты точки К, учитывая, что отрезок ВС в точке К делится пополам и, следовательно,

АК: 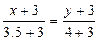или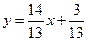

Ищем уравнение высоты АМ, опущенного из вершины А на сторону ВС :

, где .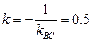

Следовательно, уравнение АМ: 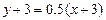или у - 0,5х +1,5 =0.

Раздел 4.

Пример 4.1. Найти область определения функции D(f)

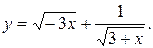
Решение. Если числовая функция задана аналитически (в виде формулы 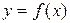) и область ее определения не указана, то считают, что эта область есть множество всех действительных значений аргумента, при которых выражение 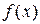- действительное число. Для существования заданной функции 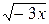необходимо, чтобы имело место неравенство 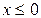. Для существования функции 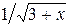должно иметь место неравенство 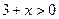, откуда . Область определения исходной функции 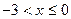или .

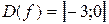Пример 4.2. Найти область определения функций:

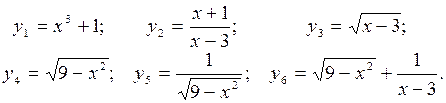
Решение. Для приведенных выше функций области определения удовлетворяют условиям:

1.

2. 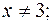3.

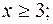
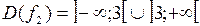
3.

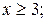
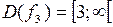
4.

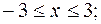
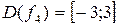
5.

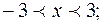
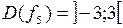
6. ;

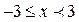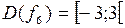
Пример 4.3. Найти область определения функции

.

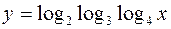Решение. Для существования функции 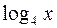необходимо, чтобы 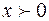. Для существования функции 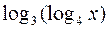надо, чтобы , откуда 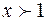. Для существования функции 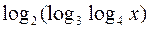необходимо, чтобы 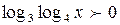, откуда и .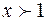

Таким образом, получены условия

.

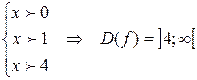Следовательно, .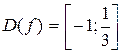

Пример 4.4. Определить, являются ли функции

1. ;

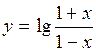2. ;

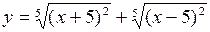3. ;

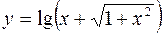4.

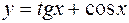
четными или нечетными.

Решение. Для определения свойств четности или нечетности функции следует проверить выполнение следующих положений:

1. Является ли область определение симметричной относительно начала координат, т.е. если 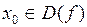, то и ;

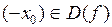2. Выполняются ли равенства 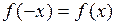или 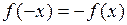. При выполнении первого равенства функция окажется четной с графиком, симметричным относительно оси ординат, во втором – нечетной с графиком, симметричным относительно начала координат.

Для указанных в задаче функций:

1. ,

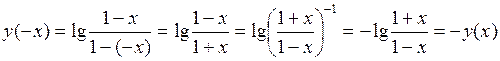то функция 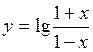- нечетная;

2. ,

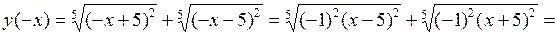
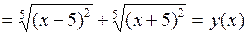то функция 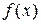является четной;

3. ,

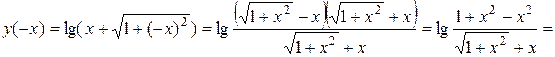
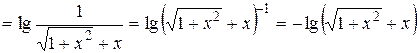следовательно, функция нечетная;

4. ,

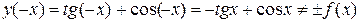следовательно, функция 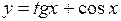не является ни четной, ни нечетной.

Пример 4.5. Найти период функции

.

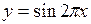Решение. При решении задач на нахождение периода функции следует использовать следующее.

Функция является периодической, если существует такое число Т¹0, что при любом x из области определения функции числа 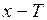и 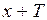также принадлежат этой области и выполняется равенство .

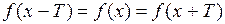В этом случае Т есть период функции .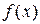

Так как 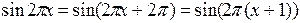, то период Т=1.

Пример 4. 6. Доказать, что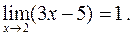

Решение. Зададим произвольное 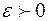и покажем, что существует положительное 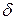такое, что из неравенства 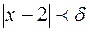вытекает неравенство .

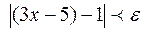Действительно,

.

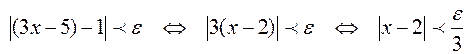Значит, если положить 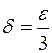, то выполнение неравенства 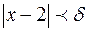влечет за собой выполнение неравенства 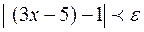. Таким образом, согласно определению, заключаем, что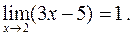

Практически предел функции находят не на основании определения предела функции, а на основании теорем о пределе функции.

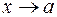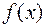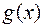Теорема. Если при существуют пределы функций и , то:

;

;

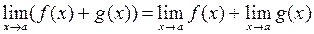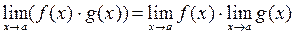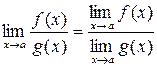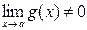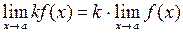, где ;

, где 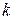- постоянный множитель.

Пример 4.7. Вычислить

.

Решение. Так как

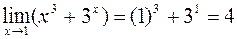, а ,

то по теореме о пределе частного получаем, что

.

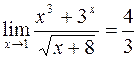Но не всегда можно применять теоремы о пределах без предварительного преобразования функций, стоящих под знаком предела. При этом возможны следующие неопределенные ситуации: , , , , .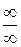

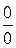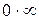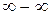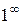Приемом раскрытия неопределенности вида 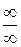является деление числителя и знаменателя на наивысшую степень x.

При неопределенности вида 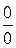требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.

Неопределенности же вида 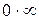и 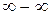путем преобразований приводят к одному из рассмотренных случав 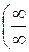или 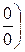. Поясним сказанное на примерах.

Пример 4. 8. Вычислить

.

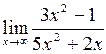Решение. Наивысшая степень x - вторая, делим числитель и знаменатель на 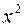. Получим

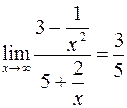, так как 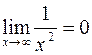и .

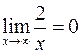Пример 4.9. Вычислить

.

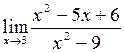Решение. Имеет место неопределенность вида 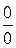. Разложим числитель и знаменатель дроби на множители. Получим

.

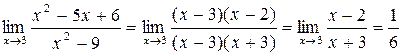Пример 4. 10. Вычислить

.

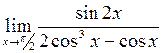Решение. Числитель и знаменатель дроби при 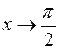стремятся к нулю. Преобразуем функцию, выделим общий множитель

.

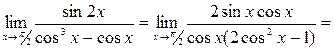
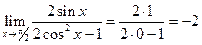Пример 4.11. Вычислить

.

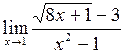Решение. Имеет место неопределенность вида 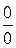. Преобразуем дробь, домножив числитель и знаменатель на выражение, сопряженное числителю

.

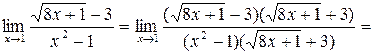
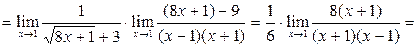
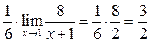Пример 4.12. Вычислить

.

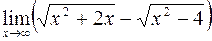Решение. Имеет место неопределенность вида 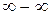. Преобразуем функцию под знаком предела, домножив и поделив на сопряженное выражение.

.

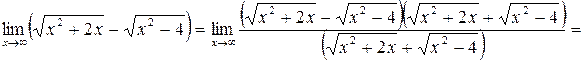
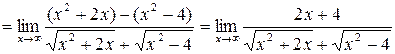Таким образом получили предел, в котором имеет место неопределенность вида 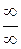. Наибольшая степень x - первая, поэтому поделим числитель и знаменатель на x, получим

.

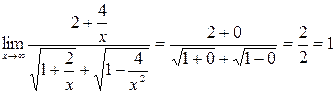Пример 4.13. Вычислить

.

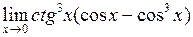Решение. Так как 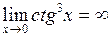, а 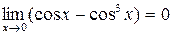, то имеет место неопределенность вида .

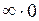Выполним преобразования

.

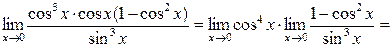
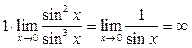Пример 4.14. Найти точки разрыва функции. Построить чертеж.

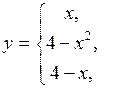если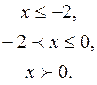

Естественно, что на интервалах 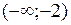, 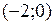и 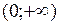функция непрерывна. Проверке подлежат только точк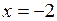и и .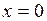

Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.

Рассмотрим точку .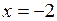

.

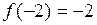Вычислим односторонние пределы

,

.

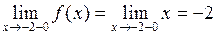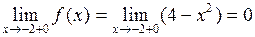Так как односторонние пределы не совпадают, 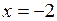- точка разрыва функции.

Рассмотрим точку .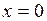

,

,

,

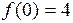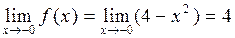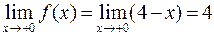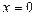- точка непрерывности функции, выполнены все условия непрерывности.

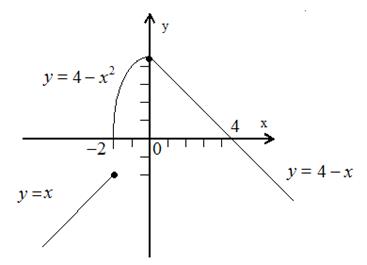
Рис. 2

Пример 4.15. Исследовать поведение функции вблизи точки разрыва. Построить схематический чертеж.

.

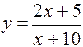Решение. Область определения функции

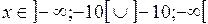. Точка разрыва .

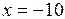Найдем односторонние пределы

; .

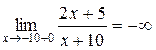Знак предела зависит от знаков числителя и знаменателя дроби. В обоих случаях числитель 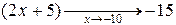, но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается положительным. Схематичный чертеж представлен на рис. 3.

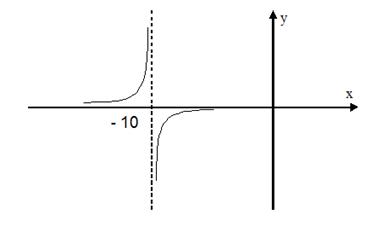
Рис. 3

Раздел 5.

Пример 5.1. Пользуясь формулами дифференцирования, найти производные следующих функций:

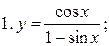
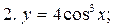
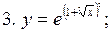4.

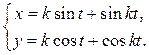
Решение.

1.

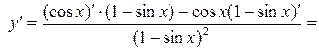
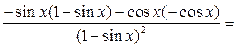
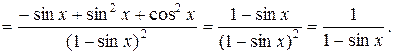
2. есть сложная функция.

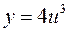, где .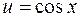

Производная сложной функции имеет вид

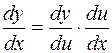или .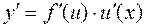

Следовательно,

.

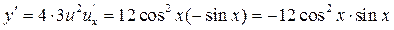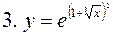- сложная функция.

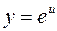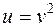, где , а ,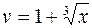

.

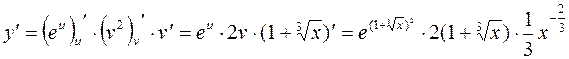5.

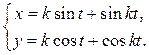
Функция 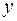от независимой переменной 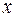задана через посредство вспомогательной переменной (параметра t). Производная от 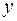по 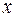определяется формулой

.

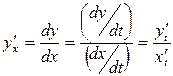Находим производные от 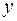и 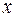по параметру t:

,

,

.

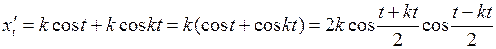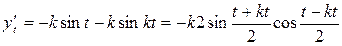Пример 5.2. Составить уравнение касательной и нормали к кривой 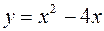в точке, где .

Решение. Уравнение касательной к кривой в точке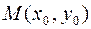

,

,

.

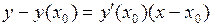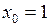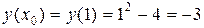Для определения углового коэффициента касательной 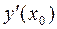находим производную

,

.

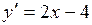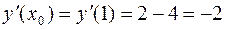Подставляя значения 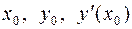в уравнение, получим

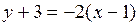или .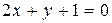

Уравнение нормали

,

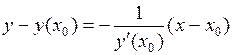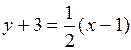или .

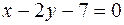Пример 5.3. Точка совершает прямолинейное колебательное движение по закону 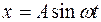. Определить скорость и ускорение движения в момент времени .

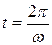Решение. Найдем скорость 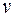и ускорение 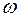движения в любой момент времени t

;

.

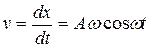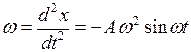При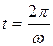

,

.

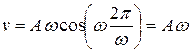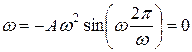Пример 5.4. Найти дифференциалы функций

1. ;

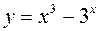2. 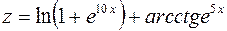, вычислить .

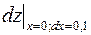Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:

1. ;

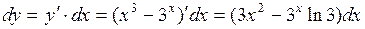2.

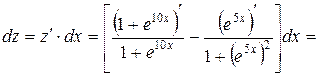
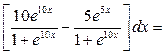
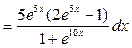
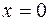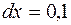Полагая и , получим .

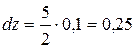Пример 5.5. Вычислить приближенное значение:

1. ;

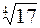2. .

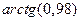Решение. Если требуется вычислить 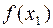и если проще вычислить и 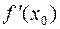, то при достаточно малой по абсолютному значению разности 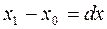можно заменить приращение функции ее дифференциалом 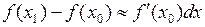и отсюда приближенное значение искомой величины по формуле

.

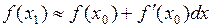1. Будем рассматривать 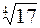как частное значение функци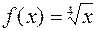и при 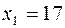. Пусть 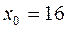, тогда

,

,

.

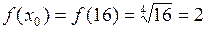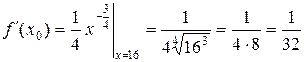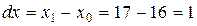Подставляя в формулу, получим

.

,

, .

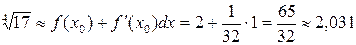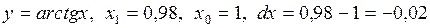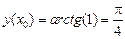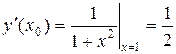Получим

.

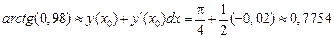Пример 5.6. Найти пределы используя правило Лопиталя

1. ;

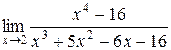2. ;

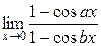3. ;

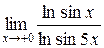4. .

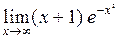Решение. Убедившись, что имеет место неопределенность 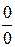или 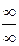, применяем затем правило Лопиталя.

1. ;

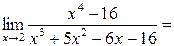
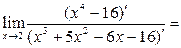
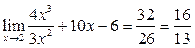2.

;

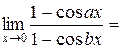
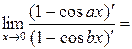
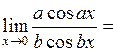
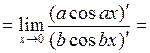
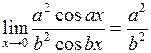здесь правило Лопиталя применено дважды.

3.

;

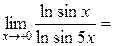
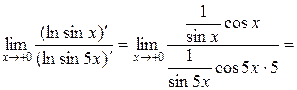
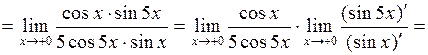
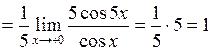4. .

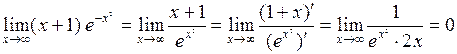Раздел 6.

Пример 6.1. Исследовать функцию 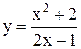и построить её график.

1. Функция определена и непрерывна в интервалах .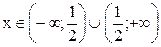

2. Функция общего вида, так как

.

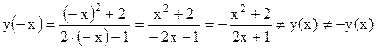3. График функции не пересекается с осью OХ, а с осью OY пересекается при x = 0, y= -2, т.е. в точке В(0; -2).

4. Исследуем функцию на наличие асимптот.

а) Уравнение вертикальной асимптоты: 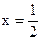. Вычислим пределы функции при 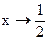слева и справа.

.

.

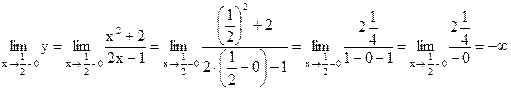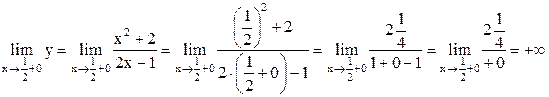б) Уравнение наклонной асимптоты имеет вид y = kx + b, где

.

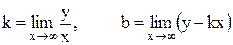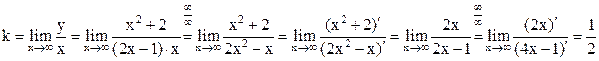
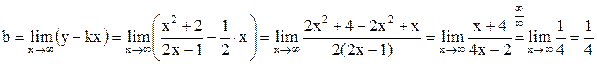
Таким образом, уравнение наклонной асимптоты .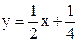

5. Исследуем функцию на экстремум.

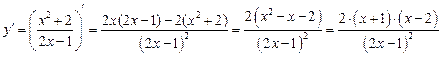
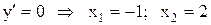- точки, подозрительные на экстремум.

Исследуем знак производной в интервалах, окружающих подозрительные точки.

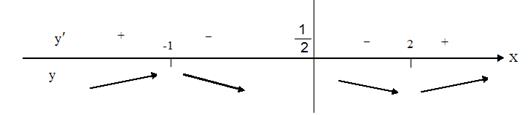
Рис. 4.

Получили, что в точке х=-1 возрастание функции сменяется убыванием, следовательно, это точка максимума. В точке х=2 убывание сменяется возрастанием, следовательно, это точка минимума (рис. 4).

; .

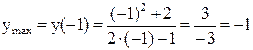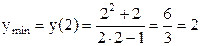6. Исследуем график функции на выпуклость и вогнутость.

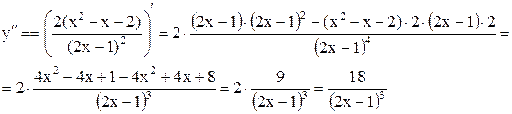
Точек перегиба нет, так как .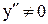

Исследуем знак второй производной в интервалах, где функция определена, (смотрите пункт 1. этого примера) (рис. 5а).

Рис. 5а.

Основываясь на полученных результатах исследования, строим график функции.

Рис. 5б

ТАБЛИЦА ПРОИЗВОДНЫХ

№			№
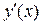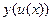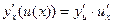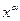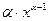			1*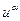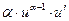
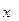			2*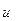
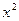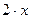			3*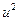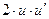
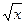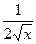			4*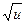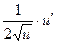
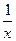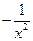			5*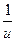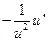
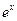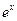			6*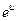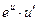
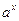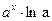			7*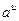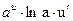
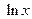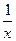			8*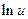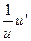
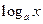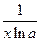			9*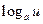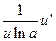
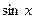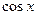			10*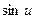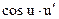
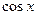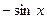			11*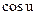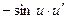
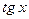			12*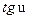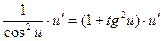
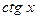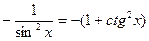			13*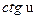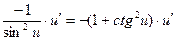
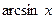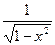			14*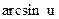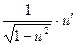
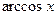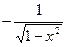			15*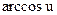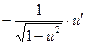
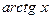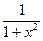			16*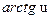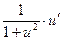
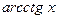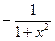			17*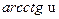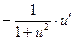

Правила дифференцирования

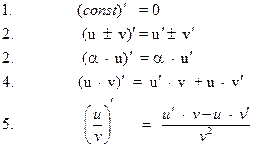
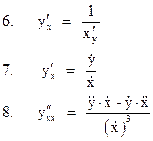
Контрольная работа 1

В задачах 1.01 – 1.20 система трёх линейных уравнений с тремя неизвестными х₁, х₂, х₃ задана своей расширенной матрицей.

Требуется:

1. записать систему в канонической форме (в виде системы уравнений),

2. решить её методом полного исключения,

3. решить систему по формулам Крамера, причём определители вычислять, используя их свойства.

1.1.	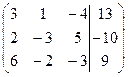.	1.11.	.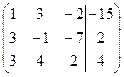
1.2	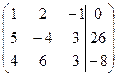.	1.12.	.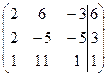
1.3.	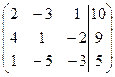.	1.13.	.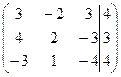
1.4.	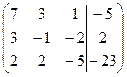.	1.14.	.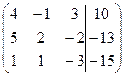
1.5.	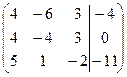.	1.15.	.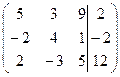
1.6.	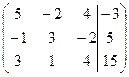.	1.16.	.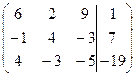
1.7.	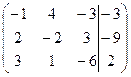.	1.17.	.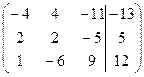
1.8.	.	1.18.	.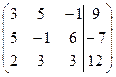
19.	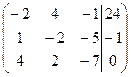.	1.19.	.
1.10.	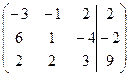.	1.20.	.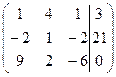

3.Даны координаты вершин пирамиды 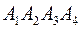, причём точка А₄ - вершина.

Средствами векторной алгебры найти:

1. длину ребра ;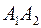

2. длину медианы основания пирамиды, проведённой из точки А₃,

3. точку пересечения медиан основания,

4. угол между ребрам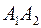и и ,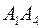

5. площадь основания пирамиды.

3.01	,	,	,	.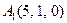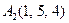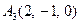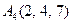
3.02	,	,	,	.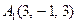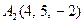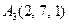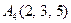
3.03	,	,	,	.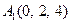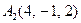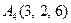
3.04	,	,	,	.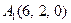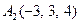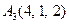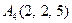
3.05	,	,	,	.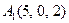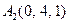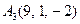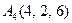
3.06	,	,	,	.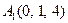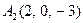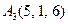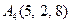
3.07	,	,	,	.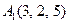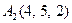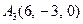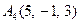
3.08	,	,	,	.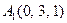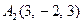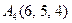
3.09	,	,	,	.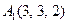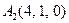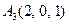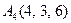
3.10	,	,	,	.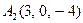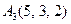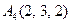
3.11	,	,	,	.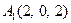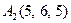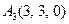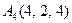
3.12	,	,	,	.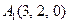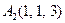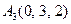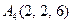
3.13	,	,	,	.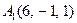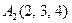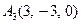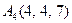
3.14	,	,	,	.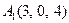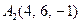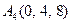
3.15	,	,	,	.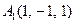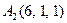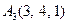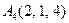
3.16	,	,	,	.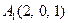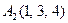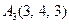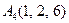
3.17	,	,	,	.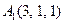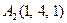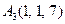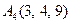
3.18	,	,	,	.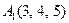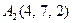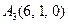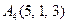
3.19	,	,	,	.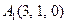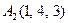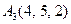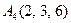
3.20	,	,	,	.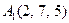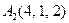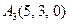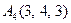

3. Треугольник АВС задан координатами своих вершин.

Сделать чертёж и найти: 1) уравнение стороны АВ,

2) уравнение стороны АС,

3) угол между этими сторонами,