Приклад 1

Миттєвою швидкістю точки, яка рухається прямолінійно, в мо­мент часу t0 називається границя середньої швидкості при умові, що Δt наближається до нуля.

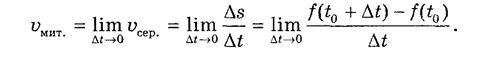
Числа Δt, Δs називаються відповідно приростом часу, прирос­том шляху.

Отже, миттєвою швидкістю точки, яка рухається прямоліній­но, є границя відношення приросту шляху Δs до відповідного приросту часу Δt, коли приріст часу наближається до нуля.

Приклад 1.

Точка рухається прямолінійно по закону s(t) = 5t² + t + 3 (s — шлях в метрах, t – час в секундах). Знайдіть швидкість точки:

а) в довільний момент t₀; б) в момент часу t = 2 с.

Розв'язання

а) 1) нехай значення аргументу t₀ одержало приріст Δt, тоді t₁ = t₀ + Δt .

2) Знайдемо відповідний приріст шляху

Δs = s(t₀ + Δt) - s(t₀) = 5(t₀ + Δt)² + (t₀ + Δt) + 3 – (5 t₀² + t₀ + 3) = 5 t₀² +10 t₀ Δt + 5Δt² + t₀ + Δt + 3 – 5t₀² – t₀ – 3 = 10t₀Δt + 5Δt² + Δt.

3) Знайдемо відношення приросту шляху до приросту часу (се­редню швидкість):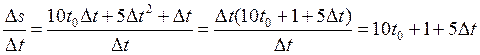

4) Знайдемо границю відношення приросту шляху до приро­сту часу (середньої швидкості):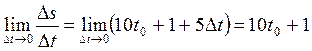

Отже, миттєва швидкість точки в довільний момент часу t₀ дорівнює 10t₀ + 1.

Отже, при заданому законі руху s(t) миттєва швидкість v(t) в довільний момент часу t обчислюється по формулі v(t) = 10t + 1.

б) Якщо t = - 2 с, то маємо v(2) = 10 · 2 +1 = 21 ;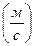

Відповідь: а) 10t + 1; б)21 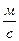.