Будь-яка підмножина з т елементів даної множини, яка містить n елементів, називається комбінацією з n елементів по т елементів
Число комбінацій з n елементів по т позначають символом 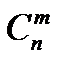 . Наприклад:
. Наприклад: 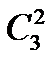 = 3.
= 3.
З чотирьох елементів множини {a, b, c, d} можна утворити 6 комбінацій по 2 елементи: {а, b}, {а, с}, {а, d}, {b, с}, {с, а}, {b. d}; 3 комбінації по 3 елементи: {а, b, с}, {а, b, d}, {b, с, d}.
Таким чином, 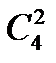 = 6,
= 6, 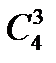 = 3.
= 3.
Домовилися вважати, що
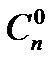 = 1,
= 1, 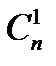 =n ,
=n , 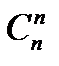 = 1.
= 1.
Виведемо формулу для знаходження значень 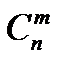 , для цього порівняємо числа
, для цього порівняємо числа 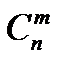 і
і 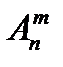 при одних і тих же значеннях т і п.
при одних і тих же значеннях т і п.
Кожну m-елементну комбінацію можна впорядкувати Рm способами. У результаті з однієї комбінації утворюється 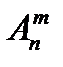 розміщень (упорядкованих підмножин) з тих самих елементів. Отже, число m-елементних комбінацій у Рm разів менше за число розміщень з тих самих елементів. Тобто
розміщень (упорядкованих підмножин) з тих самих елементів. Отже, число m-елементних комбінацій у Рm разів менше за число розміщень з тих самих елементів. Тобто 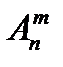 =
= 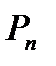 •
• 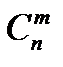 , звідси
, звідси
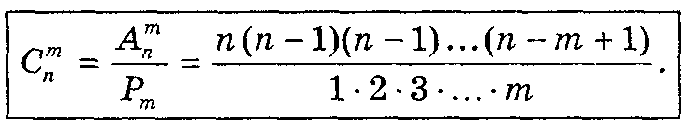
Число комбінацій з n елементів по т дорівнює дробу, чисельник якого е добуток т послідовних натуральних чисел, найбільше з яких n, а знаменник дробу — добуток т послідовних натуральних чисел.
Враховуючи, що 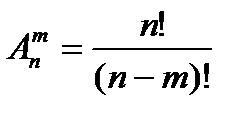 можна одержати
можна одержати 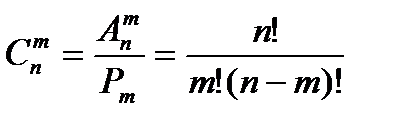 . Отже,
. Отже, 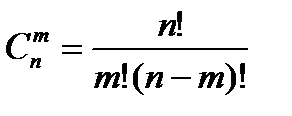
Приклад Обчислити a) 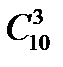 ; б)
; б) 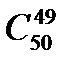 .
.
a) 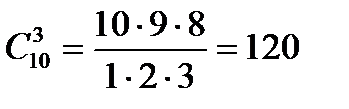 ; б)
; б) 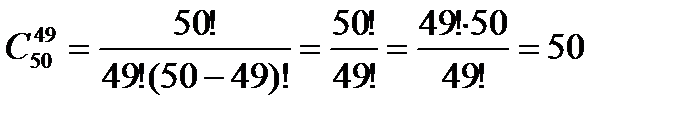
Задача. Скількома способами з 25 учнів можна вибрати 3 чергових.
