Приложения дифференциального исчисления ФОП
Вычисление определителей
1.1. Определитель 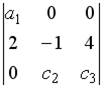 равен…
равен…
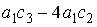 ;
; 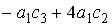 ;
; 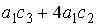 ;
; 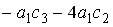
1.2. Разложение определителя  по элементам второй строки имеет вид…
по элементам второй строки имеет вид…
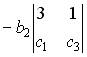 ;
; 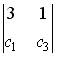 ;
; 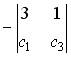 ;
; 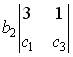
1.3. Разложение определителя 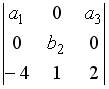 по элементам второй строки имеет вид…
по элементам второй строки имеет вид…
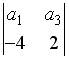 ;
; 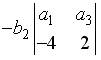 ;
; 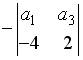 ;
; 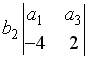
1.4. Определитель  при α равном…
при α равном…
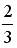 ;
;  ;
;  ; 3
; 3
1.5. Сумма целых значений параметра 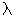 , при которых
, при которых 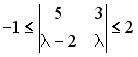 , равно…
, равно…
- 5 ; 7 ; 1 ; 18
Умножение матриц
2.1. Операция произведения матриц правильно определена для матричного умножения вида …
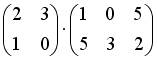 ;
; 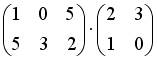 ;
; 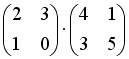 ;
; 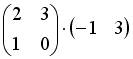
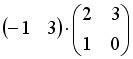
2.2. Операция произведения матриц правильно определена для матричного умножения вида …
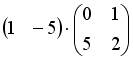 ;
; 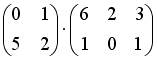 ;
; 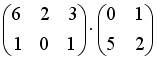 ;
; 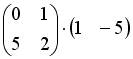
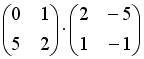
2.3. Для матриц 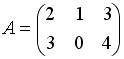 и
и 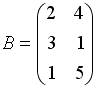 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 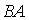 ;
; 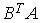 ;
; 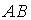 ;
; 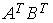 ;
; 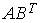
2.4. Для матриц 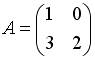 и
и 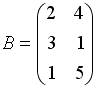 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 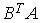 ;
; 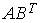 ;
; 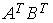 ;
; 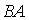 ;
; 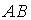
2.5. Для матриц 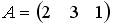 и
и 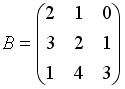 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 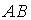 ;
; 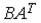 ;
; 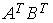 ;
; 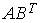 ;
; 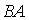
Прямая на плоскости
3.1. Даны графики прямых  :
: 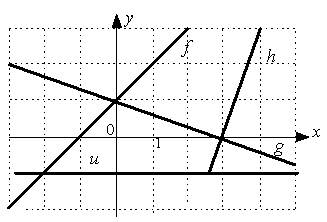
Установите соответствие между прямыми
1. f
2. g
3. h
4. u
и значениями их угловых коэффициентов:
 3 ;
3 ; 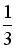 ; 1;
; 1; 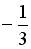 ; 0
; 0
3.2. Даны графики прямых  :
:
Установите соответствие между прямыми
1. f
2. g
3. h
4. u
и значениями их угловых коэффициентов.
1; 0; 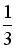 ;
; 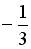 ;
; 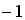
3.3. Установите соответствие между уравнением прямой и её угловым коэффициентом
1. 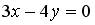 ; 2.
; 2. 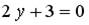 ; 3.
; 3. 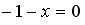
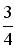 ;
; 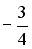 ; 0; не существует;
; 0; не существует; 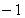
3.4. Установите соответствие между уравнением прямой и её угловым коэффициентом
1. 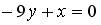 ; 2.
; 2. 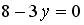 ; 3.
; 3. 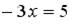
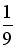 ; не существует;
; не существует; 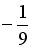 ;
; 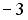 ; 0
; 0
3.5. Укажите правильное соответствие между характером расположения прямой  на декартовой плоскости и значениями коэффициентов А, В, С.
на декартовой плоскости и значениями коэффициентов А, В, С.
1. L параллельна прямой 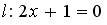
2. L параллельна прямой 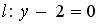
3. L совпадает с прямой 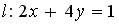
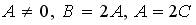 ;
; 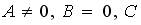 - любое;
- любое; 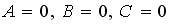 ;
;
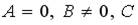 - любое;
- любое; 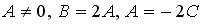
Прямая и плоскость в пространстве
4.1. Нормальный вектор плоскости 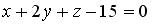 имеет координаты…
имеет координаты…
(1; 1; – 15); (1; 2; – 15); (1; 2; 1); (2; 1; – 15).
4.2. Уравнение прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 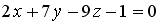 , имеет вид…
, имеет вид…
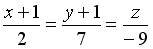 ;
;  ;
; 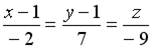 ;
; 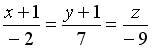
4.3. Уравнение плоскости, проходящей через точку 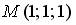 и ось
и ось 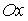 , имеет вид…
, имеет вид…
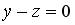 ;
; 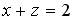 ;
; 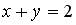 ;
; 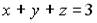 .
.
4.4. Уравнение плоскости, проходящей через точку 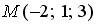 и параллельной плоскости
и параллельной плоскости 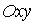 , имеет вид …
, имеет вид …
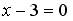 ;
; 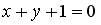 ;
; 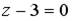 ;
; 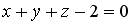 .
.
4.5. Расстояние от точки 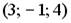 до плоскости
до плоскости 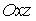 равно …
равно …
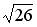 ; 1; 3; 4.
; 1; 3; 4.
Норма вектора в евклидовом пространстве
5.1. Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором
1. 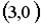 ; 2.
; 2. 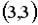 ; 3.
; 3. 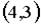 ; 4.
; 4. 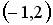
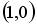 ;
; 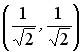 ;
; 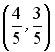 ;
; 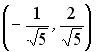 ;
; 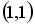 .
.
5.2. Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором
1. 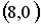 2.
2. 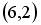 3.
3. 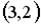 4.
4. 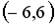
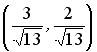 ;
; 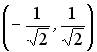 ;
; 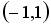 ;
; 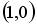 ;
; 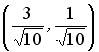 .
.
5.3. Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором
1. 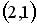 ; 2.
; 2. 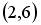 ; 3.
; 3. 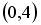 ; 4.
; 4. 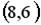
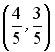 ;
; 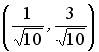 ;
; 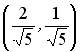 ;
; 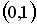 ;
; 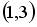 .
.
5.4. Установите соответствие между вектором и соответствующим ему нормированным вектором (ортом)
1. 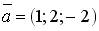 ; 2.
; 2. 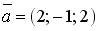 ; 3.
; 3. 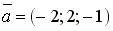
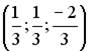 ;
; 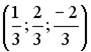 ;
; 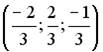 ;
; 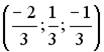 ;
; 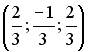
5.5. Установите соответствие между вектором и соответствующим ему нормированным вектором (ортом)
1. 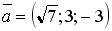 ; 2.
; 2. 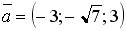 ; 3.
; 3. 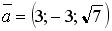
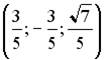 ;
; 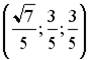 ;
; 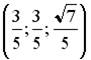 ;
; 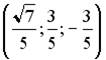 ;
; 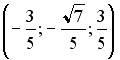
Коллинеарность и перпендикулярность векторов
6.1. Векторы 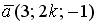 и
и 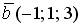 перпендикулярны, если k равно…
перпендикулярны, если k равно…
– 3; 2; 3; – 2.
6.2. Векторы 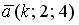 и
и 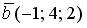 перпендикулярны, если k равно…
перпендикулярны, если k равно…
– 16; 16; – 8; 8.
6.3. Векторы 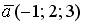 и
и 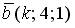 перпендикулярны, если k равно…
перпендикулярны, если k равно…
11; – 11; 10; – 10.
6.4. Векторы 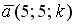 и
и 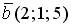 перпендикулярны, если k равно…
перпендикулярны, если k равно…
5; – 5; – 3; 3.
6.5. Векторы 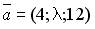 и
и 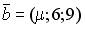 коллинеарны при …
коллинеарны при …
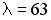 ;
;  ;
; 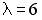 ;
; 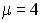 ;
; 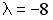 ;
; 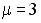 ;
; 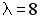 ;
; 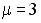 .
.
Функции, основные понятия и определения
7.1. Пусть 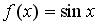 . Тогда сложная функция
. Тогда сложная функция 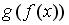 нечетна, если функция
нечетна, если функция 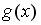 задается формулами…
задается формулами…
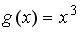 ;
; 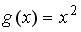 ;
; 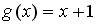 ;
; 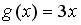 .
.
7.2. Пусть 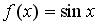 . Тогда сложная функция
. Тогда сложная функция 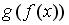 четна, если функция
четна, если функция 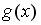 задается формулами…
задается формулами…
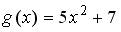 ;
; 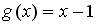 ;
; 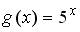 ;
;  .
.
7.3. Пусть 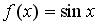 . Тогда сложная функция
. Тогда сложная функция 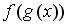 четна, если функция
четна, если функция 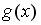 задается формулами…
задается формулами…
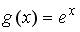 ;
; 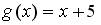 ;
; 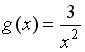 ;
; 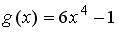 .
.
7.4. Пусть 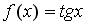 . Тогда сложная функция
. Тогда сложная функция 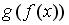 четна, если функция
четна, если функция 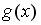 задается формулами…
задается формулами…
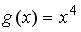 ;
; 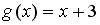 ;
; 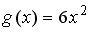 ;
; 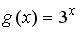 .
.
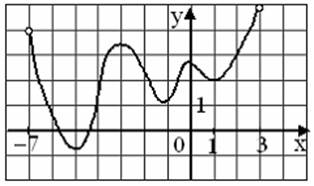
7.5. Функция 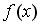 задана на отрезке
задана на отрезке 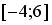 графиком:
графиком:
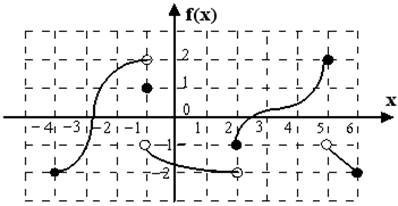
Правильными утверждениями являются…
-на промежутке 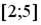 функция
функция 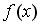 возрастает;
возрастает;
-среди значений функции 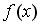 на отрезке
на отрезке 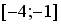 есть наибольшее и наименьшее;
есть наибольшее и наименьшее;
-при любом значении 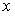 выполняется неравенство
выполняется неравенство 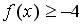 ;
;
-уравнение 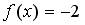 имеет три корня.
имеет три корня.
 8.Геометрический и физический смысл производной
8.Геометрический и физический смысл производной
8.1. На рисунке изображен график функции 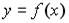 , заданной на интервале
, заданной на интервале 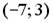 .
.
Тогда число интервалов, на которых касательная к графику функции 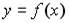 имеет отрицательный угловой коэффициент, равно …1; 3; 2; 0.
имеет отрицательный угловой коэффициент, равно …1; 3; 2; 0.
8.2. Интервалом, на котором касательная к графику функции 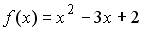 имеет положительный угловой коэффициент, является …
имеет положительный угловой коэффициент, является …
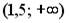 ;
; 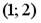 ;
; 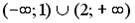 ;
; 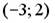 .
.
8.3. Касательная к графику функции 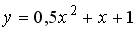 не пересекает прямую
не пересекает прямую 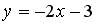 . Тогда абсцисса точки касания равна: …- 3; - 1; -
. Тогда абсцисса точки касания равна: …- 3; - 1; - 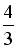 ; 2.
; 2.
8.4. Закон движения материальной точки имеет вид 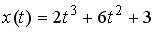 , где
, где 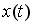 – координата точки в момент времени
– координата точки в момент времени 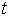 . Тогда ускорение точки при
. Тогда ускорение точки при 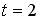 равно…
равно…
36; 10; 12; 48.
8.5. Закон движения материальной точки имеет вид 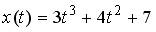 , где
, где 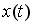 – координата точки в момент времени
– координата точки в момент времени 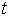 . Тогда ускорение точки при
. Тогда ускорение точки при 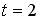 равно…
равно…
20; 44; 52; 28.
Приложения дифференциального исчисления ФОП
9.1. Наименьшее значение функции 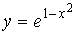 на отрезке
на отрезке 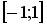 равно …(1).
равно …(1).
9.2. Наименьшее значение функции 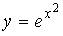 на отрезке
на отрезке 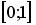 равно …(1).
равно …(1).
9.3. Наименьшее значение функции 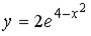 на отрезке
на отрезке 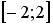 равно (2).
равно (2).
9.4. Наименьшее значение функции 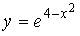 на отрезке
на отрезке 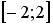 равно …(1).
равно …(1).
9.5. Наибольшее значение функции 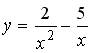 на отрезке
на отрезке 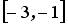 равно …(7).
равно …(7).
