Уравнение постоянства расхода в сжимаемом потоке, связь скорости и площади поперечного сечения. Сопло Лаваля.

При малых скоростях газа, когда число Маха 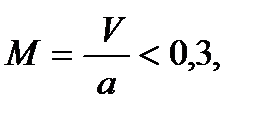движение газа можно представить как движение несжимаемой жидкости (r=const).

В этом случае уравнение постоянства расхода может быть записано

.

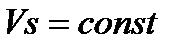Или в другой форме уравнение постоянства расхода устанавливает связь между сечением струйки и скоростью потока при М < 0,4 в виде

.

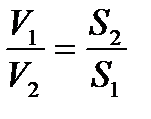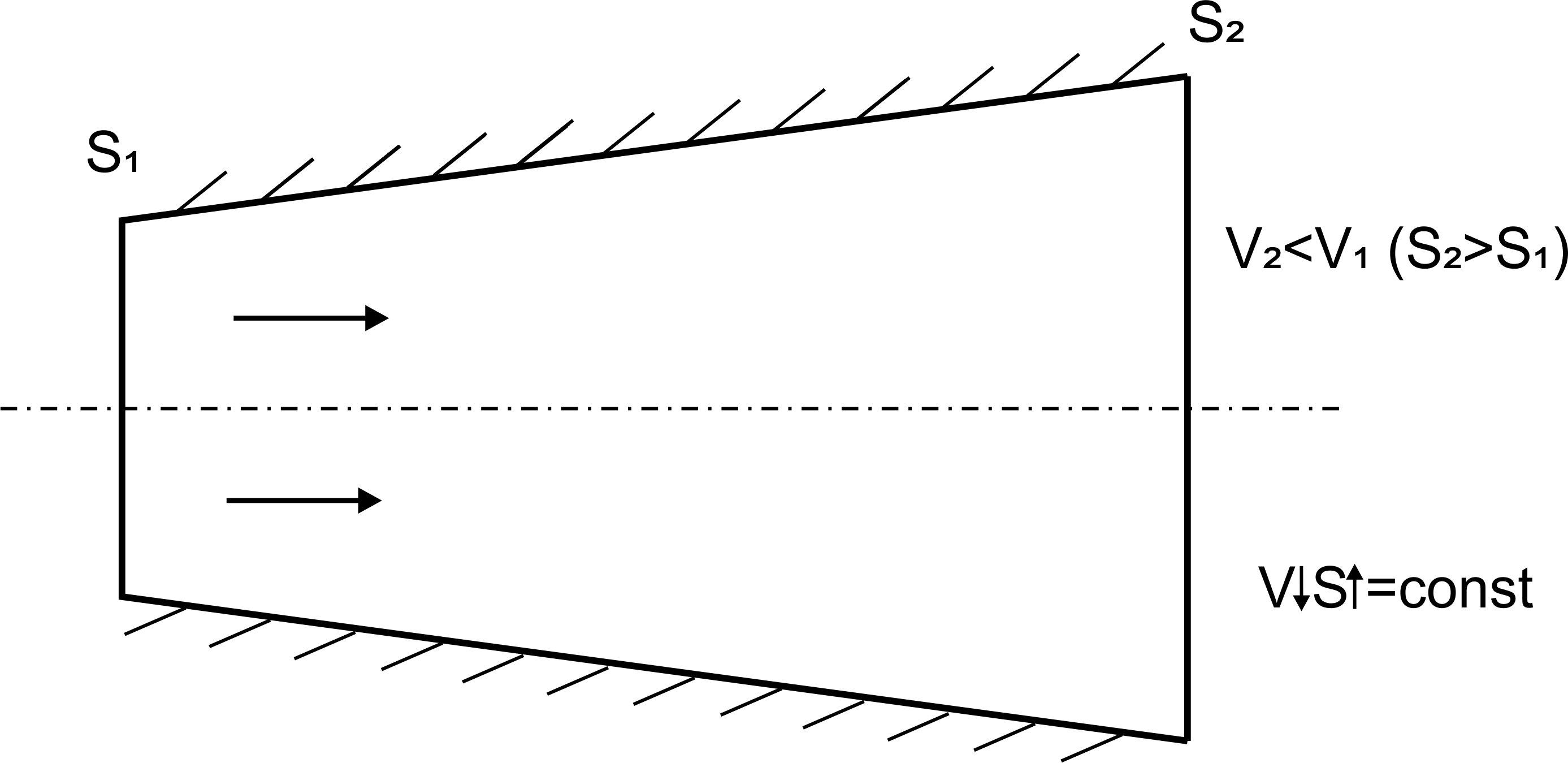
Анализ данного уравнения показывает, что для элементарной струйки или потока конечных размеров увеличение поперечного сечения, например, в таком канале, как диффузор (рис. 1.8) приводит к уменьшению скорости. Вспомним, что диффузор – это канал, который расширяется по направлению движения газа.

Рассматривая также формулу связи скорости звука и скорости газа

,

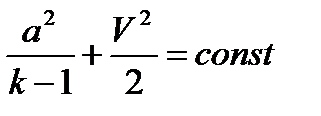можем сделать вывод, что если сечение струйки (потока конечных размеров) при числах М<0,4 уменьшается, то и скорость звука также уменьшается.

Рис. 1.8 Влияние площади поперечного сечения канала (диффузора) на скорость потока

Однако при больших скоростях полета магистральных ВС плотность воздуха начинает изменяться и уравнение постоянства расхода (по другому – уравнение неразрывности) имеет вид

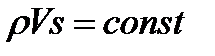. (1.14)

Прологарифмируем уравнение (1.14)

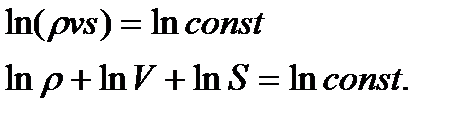
После дифференцирования получим

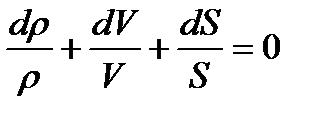. (1.15)

Умножим и разделим на dp первый член уравнения (1.15), получим V

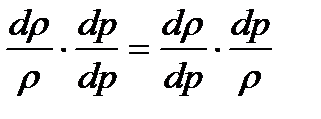. (1.16)

Используя уравнения для скорости звука

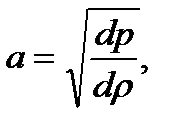
и уравнение Бернулли для газа в дифференциальном виде (формула 1.2)

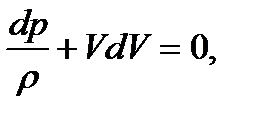
подставим их в уравнение (1.16) и получим

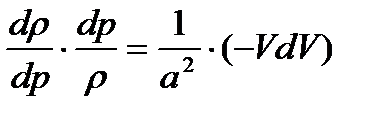. (1.17)

Подставляя (1.17) в (1.15), получим

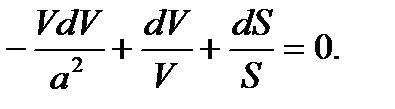
Сделаем следующие преобразования

.

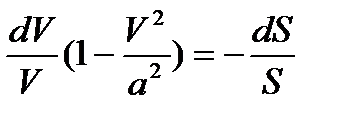Окончательно получим уравнение связи скорости и площади поперечного сечения в сжимаемом потоке

.

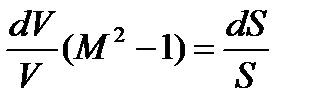Данное уравнение называется уравнением Гюгонио. Уравнение Гюгонио является частным случаем уравнения постоянства расхода.

Проанализируем с помощью уравнения Гюгонио, как влияет изменение площади сечения канала на скорость течения газа (табл. 1.2).

Рассмотрим следующие случаи (см.табл. 1.2):

№1 – течение дозвуковое (М<1), канал сужается (dS<0);

№2 – течение дозвуковое (М<1), канал расширяется (dS >0);

№3 – течение сверхзвуковое (М>1), канал расширяется (dS >0);

№4 – течение сверхзвуковое (М>1), канал сужается (dS <0).

Вывод: данные таблицы 1.2 показывают, что в сверхзвуковом и дозвуковом течениях влияние изменения геометрии на скорость потока газа является обратным.

Например, можно утверждать, что сверхзвуковая скорость потока в расширяющемся канале увеличивается в отличие от дозвукового потока, скорость которого уменьшается.

Таблица 1.2

№ п/п	Число Маха М	Изменен. площади канала dS	Геометрическая форма канала	Изменение знаков в уравн. Гюгонио	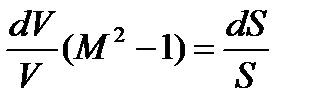Изменение скорости dV
	М<1 (дозвуковой поток)	dS<0	Сужается		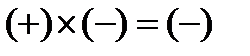dV>0 (скорость увеличив.)
2	М<1 (дозвуковой поток)	dS>0	Расширяется		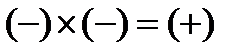dV<0 (скорость уменьш.)
	М>1 (сверхзвук. поток)	dS>0	Расширяется		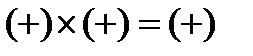dV>0 (скорость увеличив.)
	М>1 (сверхзвук. поток)	dS<0	Сужается		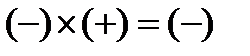dV<0 (скорость уменьш.)

Анализ уравнения Гюгонио и данных таблицы 1.2 свидетельствует, что необходимость увеличения скорости газа до сверхзвуковой требует использования сложной сужающе­-расширяющейся формы канала. Такой канал получил название сопла Лаваля (рис. 1.9).

Рассмотрим, каковы условия реализации сверхзвукового режима в сужающе–расширяющемся сопле (режима сопла Лаваля).

В таком сопле возможны четыре функциональных режима работы, что показано на рис. 1.9.

При скорости 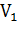на входе в сопло (1-й режима течения) не удается достичь скорости звука в области минимального сечения сопла. Тогда, согласно уравнению Гюгонио в расширяющейся части сопла Лаваля скорость дозвукового потока будет уменьшаться до скорости 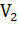.Такой режим течения используется для измерения расхода и получил название режима трубы Вентури.

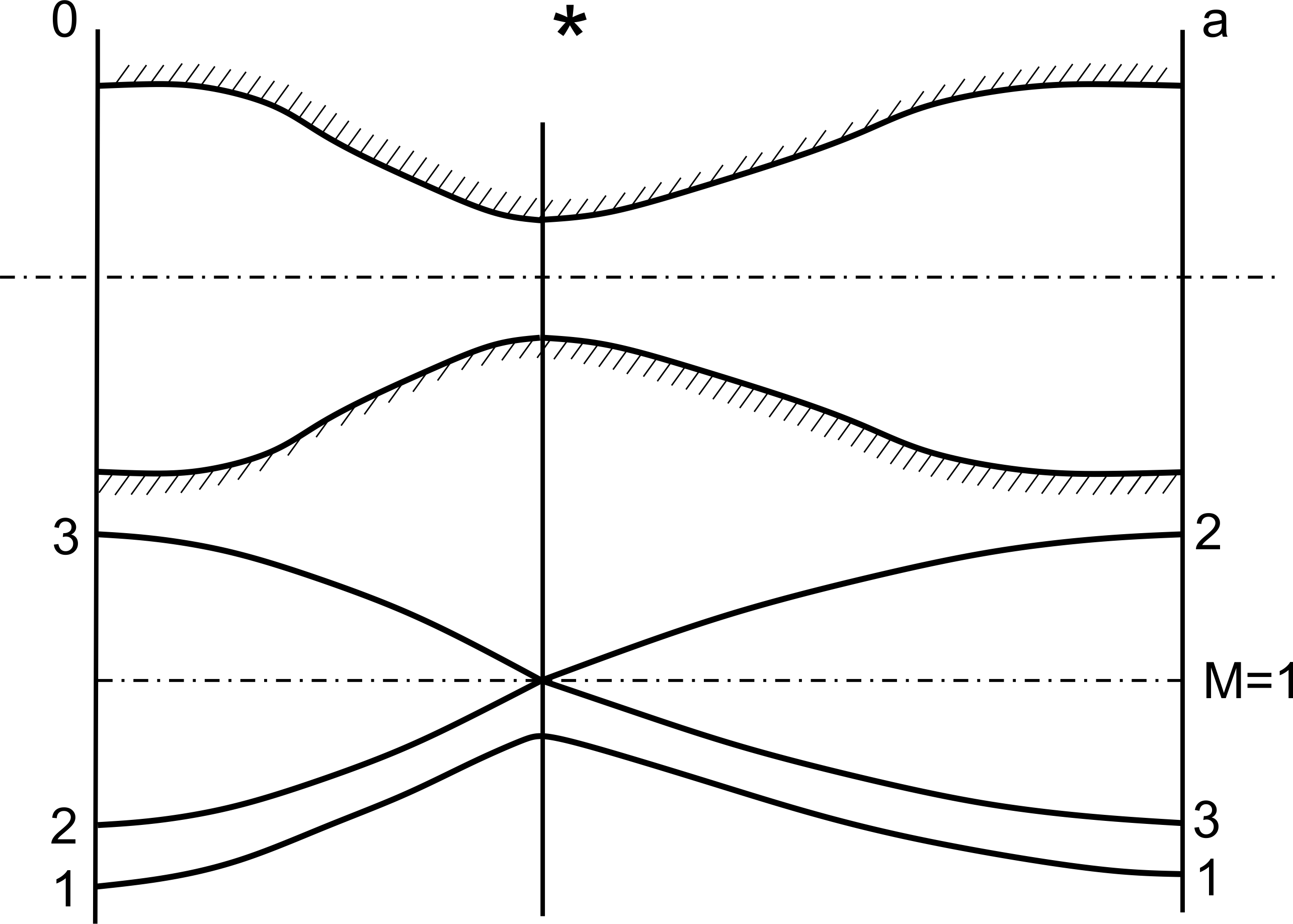
Рис.1.9 Изменение скорости по длине сопла Лаваля (4 режима течения)

В том случае, когда давление в области минимального сечения 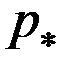определяется в соответствии с формулой

,

где e - степень расширения давления до минимального сечения сопла Лаваля, а 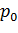– давление торможения на входе в сопло, реализуется режим сопла Лаваля. При этом скорость газа во всех сечениях возрастает, а за минимальным сечением уже превышает звуковую, т.е. становится сверхзвуковой. Это второй, основной режим течения, получивший название режима сверхзвукового истечения или режима сопла Лаваля.

Третий режим – когда на входе в сопло скорость сверхзвуковая, а в области минимального сечения она (скорость) не достигает звуковой, специального названия не имеет.

Четвертый режим, при котором в области минимального сечения сверхзвуковая скорость потока переходит в дозвуковую, носит название режима сверхзвукового диффузора и используется во входных устройствах сверхзвуковых самолетов для того, чтобы повысить давление газа на входе в компрессор двигателя.

Таким образом, принцип работы сопла Лаваля заключается в использовании сужающе-расширяющегося сопла для ускорения потока до сверхзвуковых скоростей на срезе такого сопла.

Такое сопло широко применяется в реактивных двигателях сверхзвуковых самолетов, ракетных двигателях, а также в качестве расходомерного устройства.