Принцип возможных перемещений при равновесии материальной системы. Общее уравнение статики
Пусть материальная система находится в равновесии. Силы, действующие на каждую ее точку, уравновешиваются. Если 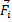 – равнодействующая всех активных сил, приложенных к i-той точке, а
– равнодействующая всех активных сил, приложенных к i-той точке, а  – реакция связей этой точки, то (рис.3)
– реакция связей этой точки, то (рис.3)
Рис.3
Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения 
Затем вычислим работу всех сил на этих перемещениях.
Так как силы, приложенные к каждой точке уравновешиваются и 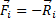 , то сумма работ этих сил на перемещении
, то сумма работ этих сил на перемещении 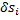 будет равна нулю:
будет равна нулю: 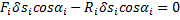 . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю
. Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю
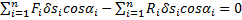 .
.
Если связи идеальные, то вторая сумма всегда равна нулю. Значит,
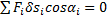 (1)
(1)
Этот результат, уравнение работ, называют общим уравнением статики.
При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю.
Конечно, если у системы есть неидеальные связи, например, с трением, или упругие, вроде пружины, то в уравнение работ надо добавить возможную работу реакций этих связей.
Принцип возможных перемещений можно записать в другой форме.
Если возможные перемещения точек определить с помощью возможных скоростей: 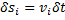 где время
где время 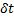 - произвольная бесконечно малая величина, то уравнение работ (1) запишется так
- произвольная бесконечно малая величина, то уравнение работ (1) запишется так 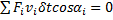 , а, поделив его на
, а, поделив его на 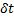 получим
получим
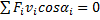 , (2)
, (2)
где 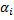 – углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.
– углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.
Равенство (2) можно назвать принципом возможных скоростей, уравнением мощностей. Оно иногда бывает более удобным, так как используются конечные величины скоростей, а не бесконечно малые перемещения.
Этот принцип, общее уравнение статики, позволяет решать задачи на исследование равновесного состояния системы, в частности – находить неизвестные реакции связей. Естественно, при этом возникает вопрос: как же так, ведь реакции идеальных связей не входят в уравнение работ? Выход прост – надо сделать тело свободным, реакции отнести к разряду активных сил и затем назначать такие возможные перемещения, чтобы эти неизвестные силы совершали работу.
Общее уравнение статики – довольно эффективный метод и применять его, конечно, надо для исследования равновесия сложных систем; хотя и при решении обычных задач статики он оказывается тоже выгодным.
Пример 1. Какую силу F надо приложить к желобу с грузом весом Р, чтобы удержать его в равновесии (рис.4)?
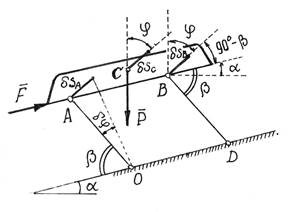
Рис.4
Решение.Эту задачу можно решить известными методами статики, составляя уравнения равновесия. Но при этом придется прежде отыскать усилия в стержнях. Принцип возможных перемещений позволяет найти силу F проще, с помощью общего уравнения статики.
Показываем активные силы 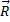 и
и 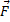 . Даем системе возможное перемещение, повернув стержень АО на угол
. Даем системе возможное перемещение, повернув стержень АО на угол 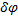 (рис.66). Так как желоб совершит поступательное движение, то перемещения всех его точек будут одинаковы:
(рис.66). Так как желоб совершит поступательное движение, то перемещения всех его точек будут одинаковы:

где a=AO=BD.
Составляем уравнение работ: 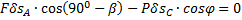 . Угол
. Угол 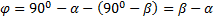 .
.
Поэтому получим 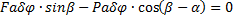 . Отсюда
. Отсюда 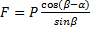 .
.
Пример 2.На рис.5 изображена конструкция, состоящая из четырех одинаковых Т-образных рам, соединенных шарнирами К, М, Q. Опоры А и Е – шарнирно-неподвижные, В и D – шарнирно-подвижные. Определим горизонтальную составляющую 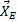 реакции опоры Е, вызванную силой
реакции опоры Е, вызванную силой 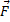 , приложенной к левой раме.
, приложенной к левой раме.
Рис.5
Решение. Методы статики дадут довольно сложное и длинное решение, так как придется рассматривать равновесие четырех рам и решать систему из 12 уравнений с 12-ю неизвестными.
Принцип возможных перемещений дает более простое и короткое решение.
Надо изменить конструкцию опоры Е. Сделаем ее подвижной, а чтобы система осталась в равновесии, приложим к опоре силу  , ту силу, которую нужно определить (рис.5,а).
, ту силу, которую нужно определить (рис.5,а).
Даем затем системе возможное перемещение, повернув левую раму вокруг опоры А на угол  . С помощью мгновенных центров скоростей С1, С2 и С3 каждой рамы, обнаруживаем, что
. С помощью мгновенных центров скоростей С1, С2 и С3 каждой рамы, обнаруживаем, что 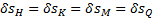 , а
, а 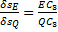 или
или 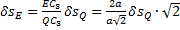 Составляем уравнение работ, общее уравнение статики,
Составляем уравнение работ, общее уравнение статики, 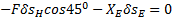 или
или 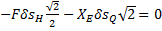 . Отсюда
. Отсюда 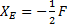 .
.
Чтобы определить вертикальную составляющую 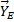 реакции опоры Е, ее надо вновь переделать (рис. 5,б), дать системе соответствующее возможное перемещение и составить уравнение работ.
реакции опоры Е, ее надо вновь переделать (рис. 5,б), дать системе соответствующее возможное перемещение и составить уравнение работ.
