Основные методы численного моделирования

ОГЛАВЛЕНИЕ

Введение...................................................................................................................3

Глава 1 Основные методы и средства моделирования взаимосвязанных электромагнитных и тепловых полей....................................................................4

1.1 Основные методы численного моделирования..........................................4

1.2 Программные средства для численного моделирования электротехнологических процессов и установок................................................7

1.3 Программный пакет FLUX.........................................................................10

1.3.1 Общие сведения о пакете FLUX................................................................10

1.3.2 Запуск программы FLUX............................................................................11

1.3.3 Предупреждения и ошибки........................................................................12

1.3.4 Организация меню.......................................................................................13

Глава 2 Физические основы процессов индукционного нагрева.....................17

2.1 Основные электромагнитные явления в процессе индукционного нагрева……………………………………………………………………..17

2.2 Основные тепловые явления в процессе индукционного нагрева….........18

2.3 Базовая математическая модель.....................................................................19

Глава 3 Задача моделирования процесса периодического индукционного нагрева в программном пакете FLUX.................................................................23

3.1 Постановка задачи...........................................................................................23

3.2 Создание системы «Индуктор - заготовка»..................................................23

3.3 Решение задачи моделирования....................................................................51

3.4 Анализ результатов расчета...........................................................................52

Глава 4 Задания для выполнения лабораторной работы...................................60

Введение

Индукционные нагревательные установки требуют комплексного анализа функциональным требованиям и условиям работы, поэтому компьютерное моделирование и анализ результатов вычислений на персональном компьютере (ПК) становятся неотъемлемой частью современного процесса модернизации установок. Для анализа процесса индукционного нагрева необходим расчёт электромагнитных полей в различных условиях, после этого осуществляется анализ функционирования устройства.

………….Метод конечных элементов является перспективным для компьютерного моделирования автомобильных датчиков, так как он является универсальным и позволяет анализировать любые включения материалов в рабочей зоне, в том числе нелинейные ферромагнитные. На современном уровне вычислительной техники может быть достигнута высокая точность моделирования.

Основные этапы конечноэлементного анализа можно представить в такой последовательности:

● построение или импорт геометрической модели (препроцессор);

● генерация сетки;

● задание физических свойств;

● процесс решения;

● обработка результатов (постпроцессор).

Среди специализированных пакетов для расчётов магнитных полей встречаются 2D и 3D конфигурации. Конфигурация 2D может использоваться в качестве демонстрационных, для выполнения более точных расчётов и объёмной визуализации геометрической модели разработчикам интересны именно трёхмерные CAD/CAE пакеты программ, причём с максимально дружественным пользовательским интерфейсом, позволяющим оператору полностью сконцентрироваться на решении задачи.

Одним из таких специализированных пакетов является FLUX, разработанный французской компанией Cedrat. Пакет предназначен для многопараметрического электромагнитного, теплового и электромеханического анализа 2D и 3D конфигураций моделей устройств.

……..

Данное методическое указание направленно на подготовку магистрантов для получения базовых знаний и навыков моделирования в программном пакете Flux.

В первой главе пособия изложены основные методы и средства численного моделирования, а также краткая информация о пакете Flux

Во второй главе кратко изложены физические основы процесса индукционного нагрева.

В третьей главе очень широко изложен алгоритм моделирования системы «Индуктор-заготовка», а также проведен анализ полученных результатов моделирования.

Глава 1 Основные методы и средства моделирования взаимосвязанных электромагнитных и тепловых полей

Основные методы численного моделирования

В последнее время упрощенным аналитическим приближениям с множеством ограничений и относительно низкой точностью все более часто приходят на смену высокоэффективные численные методы. Эти методы широко и успешно используются для решения задач электромагнитного, теплового и прочностного и других типов анализа. Каждый из этих методов имеет определенные преимущества и может использоваться один или совместно с другими.

К наиболее распространенным численным методам, прежде всего, следует отнести метод конечных разностей (МКР), метод конечных элементов (МКЭ), метод граничных элементов (МГЭ), гибридный метод.

Метод конечных разностей или, как часто его называют, метод сеток – наиболее старый и относительно простой метод, поскольку требует минимальной математической работы. МКР довольно успешно применялся и применяется в настоящее время для решения широкого круга расчета электромагнитных и тепловых полей. Идея метода конечных разностей (метода сеток) известна давно, с соответствующих трудов Эйлера. Однако практическое применение этого метода было тогда весьма ограничено из-за огромного объема ручных вычислений, связанных с размерностью получаемых систем алгебраических уравнений, на решение которых требовались годы. В настоящее время, с появлением быстродействующих компьютеров, ситуация в корне изменилась. Этот метод стал удобен для практического использования и является одним из наиболее эффективных при решении различных задач математической физики.

Основная идея метода конечных разностей (метода сеток) для приближенного численного решения краевой задачи для двумерного дифференциального уравнения в частных производных состоит в следующем:

1) на плоскости в области А, в которой ищется решение, строится сеточная область Аs (рис.2.1), состоящая из одинаковых ячеек размером s ( s – шаг сетки) и являющаяся приближением данной области А;

2) заданное дифференциальное уравнение в частных производных заменяется в узлах сетки Аs соответствующим конечно-разностным уравнением;

3) с учетом граничных условий устанавливаются значения искомого решения в граничных узлах области Аs.

Решая полученную систему конечно-разностных алгебраических уравнений, получим значения искомой функции в узлах сетки Аs , т.е. приближенное численное решение краевой задачи. Выбор сеточной области Аs зависит от конкретной задачи, но всегда надо стремиться к тому, чтобы контур сеточной области Аs наилучшим образом аппроксимировал контур области А.

Недостатками метода являются необходимость применения специальных методов хранения слабо заполненных матриц (методы, основанные на приведении матрицы к ленточному виду, методы факторизации и др.), а также сложность описания криволинейных поверхностей тел из-за применения прямоугольной конечно-разностной сетки.

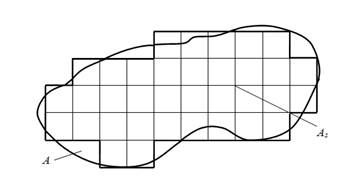
Рис. 1 – Построение сеточной области

Изначально возникновение метода конечных элементов (МКЭ) связано с решением задач космических исследований в 1950-х годах. Сама идея МКЭ была разработана в СССР ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году. Популярность МКЭ обусловлена приемлемой точностью решения, возможностью описания криволинейных границ области любой сложности, лёгкостью учета граничных условий различных типов.

Идея метода заключается в следующем: в методе взвешенных невязок воспользоваться простыми пробными и весовыми функциями, но не во всей области S, а в её отдельных подобластях (конечных элементах), а точность решения задачи обеспечить использованием большого числа конечных элементов (КЭ), при этом КЭ могут быть простой формы и вычисление интегралов по ним не должно вызывать особых затруднений. Математически переход от метода взвешенных невязок к МКЭ осуществляется с использованием специальных пробных функций, которые также называются глобальными базисными функциями, обладающих следующими свойствами:

1) в узле аппроксимации функции имеют значение равное единице;

2) отличны от нуля только в КЭ, содержащих этот узел аппроксимации, во всей остальной области равны нулю.

Этапы решения задач с общих позиций:

Таким образом, основными этапами применения МКЭ являются следующие:

Дискретизация задачи, т.е. представление области определения в виде совокупности конечных элементов, взаимосвязанных в узловых точках. При этом границы внешних элементов аппроксимируют в совокупности границу области в целом;

Получение матриц и векторов нагрузки элементов;

Формирование глобальных матриц и глобального вектора нагрузки для всей области определения;

Решение системы уравнений для узловых значений2

Расчет любой другой функции, зависящей от узловых неизвестных.

Реализация в рамках МКЭ представления области определения совокупностью конечных элементов обусловливает следующие важные преимущества МКЭ, обеспечивающие его широкое применение для решения задач теории поля:

Свойства материала каждого элемента могут быть индивидуальными и к тому же анизотропными;

Обеспечивается широкая вариация задания граничных условий на отдельных границах области;

Криволинейные границы области могут быть аппроксимированы с помощью прямолинейных элементов;

Размеры элементов могут быть переменными, как и форма самих элементов;

Обеспечивается возможность повышения точности решения задачи путем увеличения количества элементов, ограничиваемого лишь мощностью, используемой ЭВМ;

Вследствие наличия общих узловых точек, глобальные матрицы являются ленточными, т.е. содержат большое количество нулей, независимых в памяти ЭВМ.

Сравнение МКР и МКЭ

МКР и МКЭ являются сеточными методами. С точки зрения теоретических оценок точности МКР и МКЭ обладают примерно равными возможностями. Методы конечных элементов и конечных разностей имеют ряд существенных отличий. Прежде всего, методы различны в том, что в МКР аппроксимируются производные искомых функций, а МКЭ – само решение, т.е. зависимость искомых функций от пространственных координат и времени. В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в пограничных узлах. Таким образом МКР применяется для задач с простой геометрией. В МКЭ разбиение на элементы производится с учетом геометрических особенностей области, процесс разбиения начинается от границы с целью наилучшей аппроксимации её геометрии. Общей проблемой методов является высокая размерность результирующей системы алгебраических уравнений, которая частично решается путем использования высокопроизводительных ЭВМ.

Метод граничных элементов (МГЭ) – это метод решения краевых задач для дифференциальных уравнений в частных производных, появившийся в результате сочетания идей теории потенциала с методами современной теории аппроксимации. МГЭ, с точки зрения теории аппроксимации, имеет много общих черт с широко известным методом конечных элементов, но отличается от него существенным преимуществом: дискретизация осуществляется, как правило, не внутри области, в которой ищется решение, а на ее границе. Такое упрощение достигается путем точного удовлетворения исходным дифференциальным уравнениям с помощью представления решения в виде, характерном для теории потенциала. Указанные представления могут быть использованы в рамках МГЭ лишь в случае, когда известны в явном виде фундаментальные решения (или функции Грина) для рассматриваемых дифференциальных уравнений и исследованы граничные свойства соответствующих потенциалов. Путем предельного перехода на границу в формулах представления решения получаются граничные интегральные уравнения (ГИУ), которые являются основным объектом аппроксимации в МГ.