Краткая теория исследуемого явления. Если частица с массой m, обладающая зарядом q, движется в пространстве, где имеется электрическое поле с напряженностью

Если частица с массой m, обладающая зарядом q, движется в пространстве, где имеется электрическое поле с напряженностью 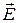, и магнитное поле с индукцией 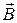, то согласно второму закону Ньютона, уравнение движения частицы имеет вид

.

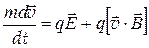Решая это уравнение при известных начальных условиях, можно найти траекторию частицы. Вид траектории зависит от 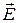, , 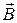а также от величины q/m, называемой удельным зарядом частицы. Зная удельный заряд, можно получить ценные сведения о природе частиц и о тех процессах, в которых они возникают.

Воздействуя на потоки электронов и ионов электрическими и магнитными полями, можно управлять этими потоками, то есть изменять их силу и направление; это лежит в основе действия многих устройств (осциллографов, телевизионных трубок, электронных микроскопов, ускорителей заряженных частиц, масс-спектрографов и т.д.).

Одним из методов определения удельного заряда электрона является «метод магнетрона». Название «метод магнетрона» связано с тем, что применяемые в ра­боте конфигурации электрического и магнитного полей по­добны конфигурации этих полей в магнетронах-генерато­рах электромагнитных колебаний в области сверхвысоких частот, применяемых в передающих устройствах радиолока­ционных станций (РЛС).

Магнетрон представляет собой двухэлектродную лампу с коаксиальными цилиндрическим анодом А и накаливаемым катодом К очень малого диаметра, помещенную внутрь соленоида, магнитное поле 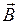которого параллельно оси лампы (рис. 1).

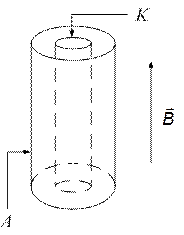
Рис. 1

При отсут­ствии электрического тока в соленоиде (при 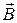=0) электроны, испускаемые раскаленным катодом вследствие электронной эмиссии, под действием электрического поля, которое возникает благодаря приложенной положительной разности потенциалов 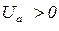между анодом (А) и катодом (К), движутся к аноду по радиусу (рис. 2, а).

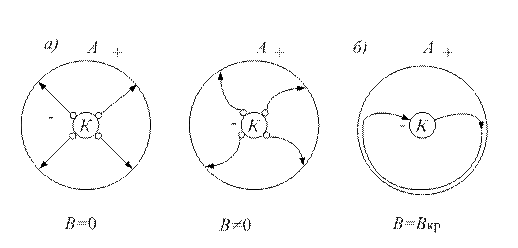
Рис. 2

Кинетическая энергия, приобретённая при этом, определяется работой сил электрического поля

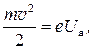(1)

где U_а – разность потенциалов; т – масса электрона; е – заряд электрона; 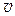– скорость его движения.

При наличии тока в соленоиде на движущиеся электроны, кроме электрической силы, со стороны магнитного поля начинает действовать сила Лоренца:

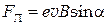(2)

где 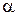– угол между векторам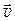и и .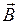

Если скорость электронов направлена перпендикулярно магнитному полю, как это имеет место в магнетроне, то фор­мула (2) принимает вид

F _Л = e 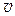B. (3)

Так как сила Лоренца перпендикулярна скорости движе­ния электрона, то под действием этой силы численное значе­ние скорости электрона не меняется, а меняется только направ­ление его движения. Траектория электрона искривляется (рис. 2, б). В случае, когда скорость электронов постоянна, а магнитное поле однородно, траектория электронов будет окружностью, а сила Лоренца – центростремительной силой:

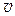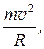e B= (4)

где R — радиус окружности.

Из совместного решения уравнений (1) и (4) можно получить формулу для расчета удельного заряда электрона:

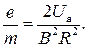(5)

В формуле (5) разность потенциалов U_а между анодом А и ка­тодом К и индукция В магнитного поля определяются из дан­ных опыта.

Радиус кривизны R траектории электрона можно опреде­лить, исходя из нижеследующих рассуждений.

При усилении магнитного поля на движущиеся электроны действует все большая сила Лоренца и траектория электронов будет все больше искривляться. При достижении некоторого «кри­тического» значения индукции магнитного поля B_кр элек­троны перестанут достигать анода лампы и по замкнутым тра­екториям будут возвращаться на катод (рис. 2, в). Анодный ток при этом должен прекратиться.