Геометриялық ықтималдық.
Оқиғаның ықтималдығын есептеу үшін, ықтималдықтың классикалық анықтамасын пайдаланып, m және n сандарын анықтау қиындыққа түседі, сондықтан оқиғаның ықтималдығын есептеу үшін, мына формуланы
қолданбайды.
Осындай жағдайларда геометриялық ықтималдық ұғымын енгізеді, нүктенің берілген облысына (кесінді, жарты жазықтық, дененің бөлігіне) түсу ықтималдығын қарастырады.
Мысалы.
l кесіндісі L кесіндісінің бөлігін құрайды. Кездейсоқ L кесіндісіне нүкте лақтырылған. Нүктенің l кесіндісіне түсуінің ықтималдығы осы кесіндінің ұзындығына тәуелді және оның осы L кесіндісі арқылы орналасуына тәуелсіз болса, онда нүктенің l кесіндісіне түсуінің ықтималдығы мына теңдікпен анықталады.
.
g жазық фигурасы G жазық фигурасының бөлігін құрайды. G фигурасына кездейсоқ нүкте лақтырылған. Нүктенің g фигурасына түсуінің ықтималдығы осы фигураның ауданына тәуелді және оның осы G фигурасы арқылы орналасуына және g фигурасының түріне тәуелсіз болса, онда нүктенің g фигурасына түсуінің ықтималдығы мына теңдікпен анықталады.
Кеңістіктегі v денесі V денесінің бөлігін құрайтын болса, нүктенің түсу ықтималдығы осылай анықталады.
.
Мысалы.
Ұзындығы 20 см кесіндінің ішіне ұзындығы 10 см кіші кесінді орналастырылған. Үлкен кесіндіге кездейсоқ қойылған нүкте кіші кесіндіге түсетінің ықтималдығын тап. Нүктенің кесіндіге түсетінінің ықтималдығы кесіндінің ұзындығына пропорционал және оның орналасуына тәуелді емес.
Шешуі:
Формулаға сәйкес
.
Дәріс №2.
Тақырыбы: «Ықтималдықтарды қосу және көбейту теоремалары. Толық ықтималдық формуласы. Бейес формуласы».
A және B оқиғалардың қосындысы немесе бірігуі деп A оқиғаның көрінуінен немесе B оқиғаның көрінуінен немесе екі оқиғаның көрінуінен тұратын оқиғаны айтады.
Оны
деп белгілейді,
немесе
С= {барлық боялған бөлігі}
Мысалы.
Қарудан екі оқ атылған. A – бірінші атқандағы оқ тию, B- екінші атқандағы оқ тию. Онда A+B – бірінші атқандағы, екінші атқандағы немесе екі атқандағы оқ тию. Егер A және B – үйлесімсіз оқиғалар болса, онда A+B осы оқиғалардың біреуінің көрінуі, қайсысының екені бәрібір.
Ықтималдықтарды қосу теоремасы. Екі үйлесімсіз оқиғаның біреуінің көріну ықтималдығы осы оқиғалардың ықтималдықтарының қосындысына тең.
.
Бірнеше үйлесімсіз оқиғалар үшін ықтималдықтарды қосу теоремасы:
.
Оқиғалардың толық тобы.
Салдар 1.
Егер A, B, C оқиғалары толық тобын құрайтын болса, онда олардың ықтималдықтарының қосындысы 1-ге тең.
Қарама - қарсыдеп толық топ құрайтын тек қана екі мүмкін оқиғалар аталады.
Белгіленуі: A және 
.
Қарама-қарсы оқиғаның ықтималдығы мынаған тең:
.
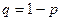Салдар 2.
A және екі қарама-қарсы оқиғаның ықтималдықтарының қосындысы 1-ге тең.
Мысал.
Жәшікте 30 шарлар бар: 10 қызыл, 5 көк және 15 ақ. Кездейсоқ алынған шар боялған болатынының ықтималдығын табыңыз.
Шешуі:
Боялған шардың пайда болуы, не қызыл, не көк түсті шардың пайда болғанын білдіреді.
А оқиғасы арқылы – қызыл түсті шардың, ал В оқиғасы арқылы – көк түсті шардың пайда болуын белгілейміз. Сонда:
;
.
А және В оқиғалары үйлесімсіз (бір түсті шардың пайда болуы, басқа түсті шардың пайда болуын жоққа шығарады), сондықтан бұл жағдайда қосу теоремасы қолданбалы:
.