Тема 6. РЯДЫ ДИНАМИКИ И ПРОГНОЗИРОВАНИЕ

Методические указания

Понятие о рядах динамики

Ряд динамики (динамический ряд) − ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение социально-экономических явлений и процессов во времени.

Динамический ряд состоит из двух основных элементов – времени (периоды или конкретные даты) и значения показателя (уровень ряда), характеризующего изучаемый объект за эти периоды или на эти даты. Уровни ряда могут быть абсолютными, относительными или средними величинами.

Ряды динамики бывают:

1) моментные – уровни такого ряда характеризуют состояние явления на конкретную дату (момент времени). Так как в каждом последующем уровне полностью или частично содержится значение предыдущего уровня, то суммировать уровни такого ряда нельзя, это приводит к повторному счёту (например, списочная численность работников предприятия на начало месяца).

2) интервальные (периодические) – уровни такого ряда характеризуют размер явления за конкретный период времени (день, месяц, год). В последующих периодах не содержатся значения признака предыдущего периода. Поэтому уровни интервального ряда можно суммировать, что позволяет получать ряды динамики укрупнённых периодов (от месячных перейти к квартальным годовым). Такой ряд можно представить как ряд с нарастающим итогом.

По расстоянию между уровнями различают ряды динамики:

1) с равностоящими уровнями – уровни, такого ряда расположены через равные следующие друг за другом интервалы времени;

2) с неравностоящими уровнями – уровни такого ряда расположены через неравные по своей продолжительности интервалы времени.

Важным моментом анализа изменений во времени является сопоставимость уровней ряда динамики.

Показатели ряда динамики

Для изучения интенсивности изменения уровней ряда во времени исчисляют следующие показатели динамики: абсолютные приросты, коэффициенты роста, темпы роста, темпы прироста, абсолютное значение одного процента прироста.

Перечисленные показатели динамики можно определять с переменной и постоянной базой сравнения. Если производится сравнение с предыдущим уровнем ряда, то получаемые показатели называются цепными (с переменной базой сравнения). Если каждый уровень сравнивается с начальным уровнем или с уровнем, принятым за базу сравнения, то получаются базисные показатели динамики (показатели динамики с постоянной базой сравнения).

Методы расчёта показателей динамики представлены в следующей таблице:

Наименование показателя	Метод расчёта
с переменной базой (цепные)	с постоянной базой (базисные)
1 Абсолютный прирост (∆y)	= yi − yi-1	= yi − y1
2 Коэффициент роста (Kр)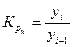
3 Темп роста (Tp), %
4 Темп прироста ( ), %
5 Абсолютное значение 1% прироста (А)	;	;

где y_i − уровень текущего периода (кроме первого);

y_i-1 − уровень периода, предшествующего текущему;

− уровень, принятый за постоянную базу сравнения (обычно первый уровень ряда).

Если в качестве базы сравнения используется отдалённый период, то для характеристики динамики явлений применяется такой показатель, как процентные пункты роста. Пункты роста (Пр) представляют собой разность темпов роста с постоянной базой сравнения двух смежных периодов.

Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики:

Показатель	Метод расчёта
1. Средний уровень ряда : а) интервального
б) моментного с равными интервалами
в) моментного с неравными интервалами
2. Средний абсолютный прирост	или
3. Средний коэффициент роста	;
4. Средний темп роста ( %)
5. Средний темп прироста (%)	или
6. Средняя величина абсолютного значения 1% прироста ( )

где – уровни последовательных периодов (дат);

n – число уровней ряда;

t – продолжительность периода, в течение которого уровень не изменялся.

В статистическом анализе при сопоставлении стохастически взаимосвязанных рядов динамики, характеризующих различные социально-экономические явления, рассчитывают коэффициент опережения (замедления). Он показывает во сколько раз один ряд динамики растёт (уменьшается) быстрее другого и определяется сопоставлением коэффициентов роста (темпов прироста) двух рядов:

или

где К_р (>)– больший коэффициент роста;

К_р(<) – меньший коэффициент роста;

Т_пр (>) – больший темп прироста;

Т_пр (<) – меньший темп прироста.