Линейная зависимость векторов

Пусть задано множество векторов в линейном пространстве L

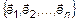(1)

и некоторый ненулевой (если хотя бы одна из 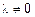) набор чисел

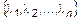. (2)

Определение 1.

Вектор 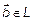называется линейной комбинацией векторов системы (1), если он равен сумме попарных произведений векторов системы (1) с соответствующим числом набора (2).

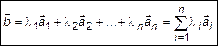(3)

ПРИМЕР 1.

.

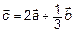Определение 2

Система векторов (1) называется линейно-зависимой, если существует ненулевой набор чисел (2), такой, что линейная комбинация векторов (1) равна нуль-вектору.

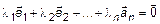. (4)

Если же равенство (4) выполняется только при всех 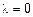, то система векторов (1) называется линейно-независимой.

ПРИМЕР 2.

Для векторов 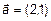, , 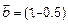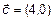запишем: 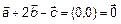, , 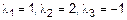следовательно векторы 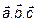- линейно-зависимы.

Замечание !!!

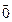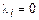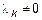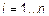Если среди векторов системы (1) есть хотя бы один , система линейно-зависима. Пусть , для и 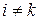. Пусть 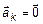по условию. Тогда 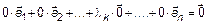, следовательно, система (1) линейно-зависима.

Теорема 1 (критерий линейной зависимости векторов).

Для того чтобы система векторов была линейно-зависима, необходимо и достаточно, чтобы какой-нибудь вектор системы можно было представить в виде линейной комбинации других векторов системы.

Доказательство.

Необходимость. Дана линейно-зависимая система (1). Требуется доказать, что 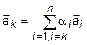. Из определения 2 следует, что

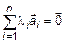(5)

при ненулевом наборе 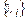. Пусть 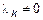. Из (5) можно найти :

.

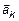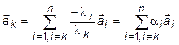Достаточность. Дано

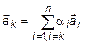. (6)

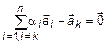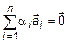Требуется доказать, что система (1) линейно-зависима. Из (6) следует, что , , а так как 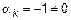, то набор (2) ненулевой, а система (1) линейно-зависима.

Следствие!!!

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарные, т. е. 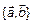– линейно-зависимы 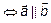, т. к. по условию коллинеарности следует, что 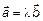, откуда по теореме 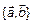– линейно-зависимы.

2. Условия линейной зависимости векторов

Теорема 2.

Три вектора линейно-зависимы тогда и только тогда, когда они компланарны, т. е. 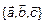– линейно-зависимы .

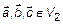Доказательство.

Необходимость. Дано 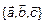– линейно-зависимы. Доказать: 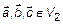. Из теоремы 1 следует, что 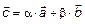, где 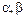– числа. По определению 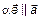, , 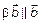следовательно, 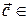пл. ( ), .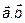

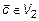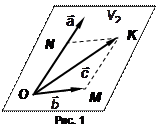
Достаточность. Дано: 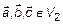. Доказать, что 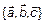– линейно-зависимы. Представим три вектора в одной плоскости (рис.1). На основаниях векторов 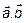построим параллелограмм так, чтобы вектор 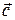был диагональю этого параллелограмма ONKM. Тогда 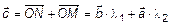, следовательно, по теореме 1 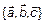– линейно-зависимы.

Теорема 3

Любые четыре вектора в 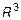линейно-зависимы.

Доказательство.

Изобразим произвольно 4 вектора 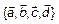в пространстве. По рис. 2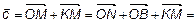 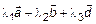. Следовательно, по теореме 1, 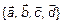– линейно-зависимы.

3. Базис пространств

Дана система векторов в L 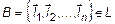. (7)

Определение 3.

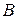Система B называется полной, если ее объединение с любым вектором этого пространства образует линейно-зависимую систему. – полная, если 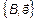– линейно-зависимы, , .

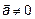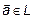Определение 4.

Полная, линейно независимая система векторов в пространстве называется базисом этого пространства.

ПРИМЕР 3.

Есл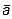и и 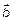не коллинеарные, то в 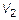они образуют базис. По определению они линейно-независимые. Это полная система потому, что присоединение 3-го вектора приведет к образованию трех компланарных векторов в 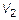, а следовательно, согласно теореме 2 они линейно-зависимы.

Следствие !!!

Из теоремы 1 и определения 4 следует, что любой вектор 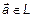можно представить в виде линейной комбинации базисных векторов:

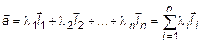. (8)

Выражение (8) называется разложением вектора в данном базисе, а числа 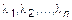– координатами 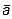в базисе B: 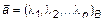. В чаще всего принимают базис, векторы которого ортогональны.

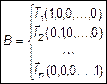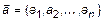, . (9)

Теорема 4 (единственности разложения вектора в базисе).

Разложение вектора в данном базисе единственно.

Доказательство (от противного).

Предположим, что верно (8) и верно

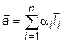, (10)

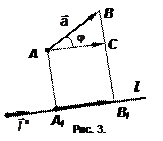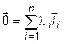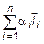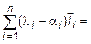
где хотя бы для одного i. Вычтем из (8) равенство (10) - = 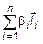. Следовательно, система B линейно-зависима, а это противоречит тому, что система B – базис. Предположение не верно, т. е. 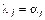для любых i, значит, разложение единственное.

Определение 5.

Число векторов базиса называется размерностью пространства.

Следствие!!!

Из теоремы 2 следует, что 3 некомпланарных вектора образуют базис (трехмерное пространство).

4. Элементы теории проекций

Определение 6.

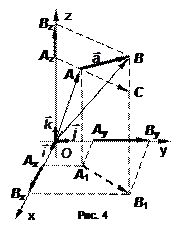Проекцией вектора 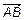на ось l ,если он сонаправлен с вектором 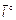, называется число, равное длине вектора 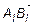, и противоположное число, если направление противоположно 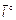( 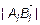, есл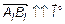и , и - 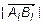, если ).

= ,

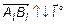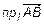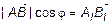где .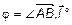

Теорема 5. .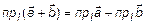

Теорема 6. .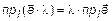

5. Декартов базис

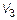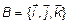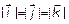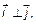
В за базис примем , где ; 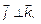, 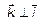– декартов базис. Тогда любой вектор 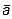можно разложить в этом базисе (рис. 4).

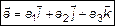, (11)

где 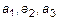– координаты 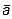в базисе.

Теорема 7.

Координаты вектора равны проекциям на соответствующие оси.

Из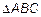

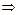
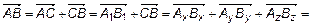
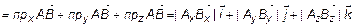. (12)

Согласно теореме 4 данное разложение (12) единственное. Из 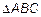по определению нормы в 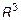следует, что 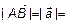, , 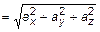где , , .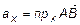

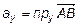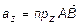Определение 7.

Радиус-вектором точки называется вектор, соединяющий начало координат с этой точкой. Обозначается для точки 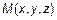как ; .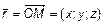

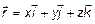Пусть даны точк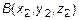и и 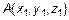. Их соответствующие радиус-векторы равны 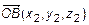и 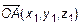(рис. 4). Из 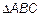получим 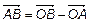. Для проекции на Ox имеем

.

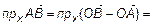
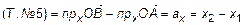Аналогичные рассуждения можно провести для остальных проекций. Тогда получим:

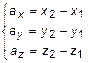(13)

Теорема 8.

Координаты вектора равны разности координат конца и начала вектор:

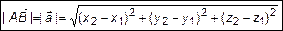. (14)

6. Полярная система координат

В полярной системе координат вектор задается следующим образом. Задается его длина 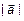и угол 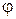поворота, отложенный от положительного направления оси 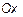. Положительный угол считается при повороте против часовой стрелки. Задать вектор в полярных координатах означает задать его норму и угол (рис. 5). То есть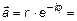 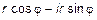– формула Эйлера, где i= 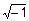– мнимая единица. Данные вопросы относятся к теории комплексных чисел и будут изучаться позже. В соответствии с рис. 5 можно привести формулы, связывающие декартову и полярные системы координат: 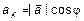, 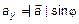. Окончательно получим

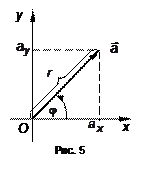
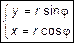. (15)

Заключение

В лекции векторная алгебра освящена на более высоком уровне. Декартова система координат представлена на основе теории проекций. Это дает более глубокое понимание вектора в трехмерном пространстве. Введено фундаментальное понятие «базис». Отметим следующее:

- размерность пространства определяется его базисом;

- линейная зависимость означает возможность представить один вектор в виде линейной комбинации других векторов;

- базис может быть и не ортогональным;

- разложение в данном базисе единственное;

- существуют другие системы координат.

Литература

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.

3. Шнейдер В.Е. и др. Краткий курс высшей математики. – М.: Высшая школа, 1998.

4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

5. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.

6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, – 659 с.

7. Фихтенгольц Г.М. Основы математического анализа. Часть 1. – М.: Лань, 2002, – 440 с.

Лекция 7

Эвклидово пространство

1. Понятие «эвклидово пространство»