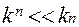Резонатор круглого сечения
Другой тип объемного резонатора – это резонатор круглого сечения, который получается из отрезка круглого волновода, стенки которого тоже закорочены.
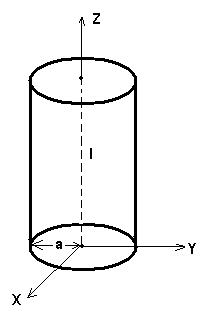
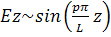
Собственные частоты объемного резонатора круглого сечения: 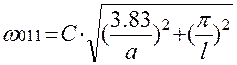
4.3 Элементы общей теории объёмных резонаторов
Общая теория объемных резонаторов строится на основе однородной системы уравнений Максвелла:
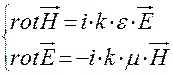
Из общей теории резонаторов следуют следующие свойства:1) собственные частоты резонатора действительные, в случае если стенки, идеально проводящие и если выполняется граничное условие 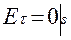 (
( 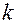 и
и 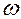 действительны числа) 2)собственные колебания для различных наборов
действительны числа) 2)собственные колебания для различных наборов 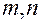 и
и 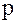 ортогональны, математически это означает:
ортогональны, математически это означает: 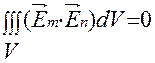 , если
, если 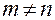
Если 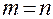 , то получим:
, то получим: 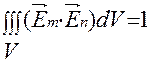
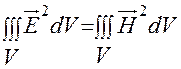
Колебания 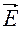 сдвинуты относительно
сдвинуты относительно 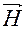 на
на 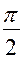
Получить эти свойства можно путем использования соотношения: 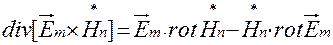
Используя это соотношения, и уравнения Максвелла мы сможем получить все эти свойства.
Если поверхность волновода не идеально проводящая, то волновые числа собственных колебаний являются комплексными величинами 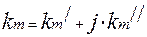 . Мнимая часть определяет потери. Добротность будет функцией
. Мнимая часть определяет потери. Добротность будет функцией 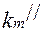 . Чем больше
. Чем больше 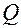 , тем меньше
, тем меньше 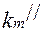 .
.
5. Возбуждение объёмных резонаторов
Основными элементами для возбуждения объемных резонаторов являются диполь, который размещается в точке где есть пучность напряженности электрического поля того типа колебания, которое необходимо возбудить.
Петля – магнитный диполь, размещающийся в пучностях напряженности магнитного поля, того типа колебания, которое необходимо возбудить.
Щель – отверстие на стенке объемного резонатора, она должна прорезаться таким образом, чтобы она пересекала поверхностный ток того типа колебания, которое необходимо возбудить.
Теория возбуждения объемных резонаторов основана на решении неоднородной системы уравнений Максвелла (система, содержащая сторонние токи возбуждения).
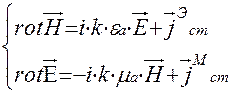
Основным путем решения системы уравнений Максвелла является представление искомого решения вынужденных колебаний объемного резонатора в виде бесконечной суммы, определяющее разложение искомого решения по собственным колебаниям объемного резонатора. Это возможно, потому что функции, описывающие собственные колебания объемного резонатора составляют полную ортонормированную систему функций:
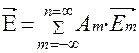
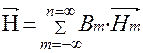
Если умножить все члены ряда 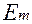 скалярно, то все члены ряда обратятся в
скалярно, то все члены ряда обратятся в 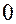 , кроме
, кроме 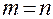 , это и есть амплитуда вынужденного колебания, которое возбуждается сторонним током.
, это и есть амплитуда вынужденного колебания, которое возбуждается сторонним током.
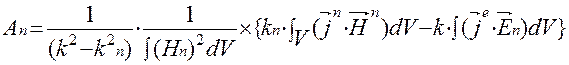
Замечание: Если стенки объемного резонатора имеют конечную проводимость, то собственные волновые числа колебаний в объемном резонаторе не являются действительными числами, а именно являются комплексными.
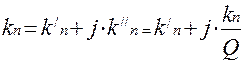
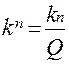 ,
,