Краткая теория. Исследование цепей постоянного тока с помощью правил Кирхгофа
Исследование цепей постоянного тока с помощью правил Кирхгофа
Методические указания к лабораторной работе №5
Ростов-на-Дону
Составители: ст. преп., к.т.н. А.Г. Краснобаев
доц., к.т.н. Р.И. Смирнова
УДК 537 (076.5)
Исследование цепей постоянного тока с помощью правил Кирхгофа: Метод. указания / Издательский центр ДГТУ.
Ростов-на-Дону. 2007. 11 с
Методические указания предназначены для организации самостоятельной работы студентов при подготовке к лабораторному практикуму и рейтинговому контролю
Печатается по решению методической комиссии факультета «Автоматизация и информатика»
Научный редактор: проф., д.т.н. В.С. Кунаков
© Издательский центр ДГТУ, 2007
Исследование цепей постоянного тока с помощью правил Кирхгофа
1. Цель работы: 1) Ознакомиться с основными характеристиками
электрического тока; 2) проверить правила
Кирхгофа.
2. Приборы и оборудование: два источника постоянного тока,
набор резисторов, вольтметр.
Краткая теория.
Электрическим током называется упорядоченное (направленное) движение электрических зарядов. Различают два вида электрических токов: токи проводимости и конвекционные токи.
Электрическим током проводимости называется упорядоченное движение в среде под действием электрического поля свободных заряженных частиц – носителей тока (например, токи в металлах, электролитах, ионизированных газах, полупроводниках, пучки электронов или ионов в вакууме).
Конвекционный ток – электрический ток, обусловленный движением в пространстве заряженных макроскопических тел (например, движущихся заряженных капель дождя, движущаяся заряженная лента электростатического генератора, изготовленная из диэлектрического материала).
Для осуществления в среде тока проводимости необходимо выполнение следующих двух условий: во-первых, в среде должны быть носители тока и, во-вторых, в ней должно существовать электрическое поле.
Носителями тока в металлах являются электроны проводимости. Если в цепи на носители тока действуют только силы электростатического поля, то это всегда приводит к такому перераспределению свободных зарядов в проводнике, при котором потенциалы во всех его точках выравниваются, и электрическое поле в проводнике исчезает. Таким образом, электростатическое поле не может поддерживать в провод-нике постоянный электрический ток. Для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счёт работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Источниками тока могут быть гальванические элементы, аккумуляторы, электрические генераторы и т.п.
Рассмотрим характеристики электрического тока. Количественной мерой электрического тока является сила тока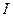 
– скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: = 
.
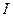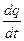Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Для характеристики направления электрического тока в разных точках рассматриваемой поверхности и распределения силы тока по этой поверхности вводится понятие вектора плотности тока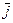 
. Вектор 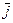направлен вдоль тока и численно равен силе тока, проходящего через единицу площади поперечного сечения проводника, перпендику-лярного направлению тока: 
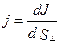, (1)
где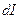 
- сила тока, проходящего через элементарную площадку 
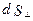, расположенную перпендикулярно к направлению вектора .
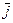Согласно закону Ома в дифференциальной (локальной) форме, плотность тока в проводнике пропорциональна напряжённости электрического поля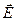 
: 
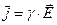, (2) 
где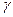 
- удельная проводимость (величина, обратная удельному сопротивлению 
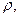т.е.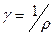 
).
|
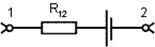
Рис .1
Под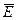 
в общем случае следует понимать напряжённость результи-рующего электрического поля, равную векторной сумме напряжённости поля кулоновских сил 
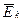и напряжённости поля сторонних сил 
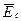, т.е.
.
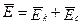Подставим данное выражение в формулу (2), получим
.
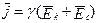Заменяем плотность тока 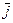через силу тока I по формуле (1), полученное уравнение интегрируем по длине участка цепи 1 – 2 (между сечениями цепи 1 – 2) с учётом того, что сила тока во всех сечениях цепи одинакова
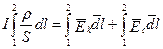, (3)
где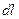 
- элемент длины проводника.
Рассмотрим физический смысл всех членов, входящих в уравнение (3). Первый интеграл, стоящий в правой части уравнения, численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда вдоль участка цепи 1 – 2 , следовательно, равен разности потенциалов (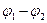 
), где 
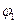и 
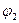- потенциалы в сечениях 1 и 2.
Второе слагаемое в формуле (3) численно равно работе, совершаемой сторонними силами при перемещении единичного положительного заряда по участку цепи 1 – 2. Эта работа производится за счёт энергии, затрачиваемой в источнике тока. Её называют электродвижущей силой источника тока (ЭДС), включённого на участке цепи 1 – 2
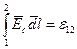, где
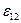- ЭДС источника тока.
Напряжением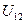 
на участке цепи 1 – 2 называется физическая величина, численно равная суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку цепи 1 - 2 единичного положительного заряда:
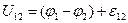. (4)
Интеграл в левой части формулы (3) называется электрическим сопротивлением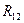 
участка 1 – 2. Для однородного проводника постоянного сечения ( 
, 
)
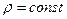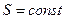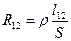, (5)
где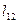 
- длина проводника между сечениями 1 – 2.
Из соотношений (3) – (5) следует, что
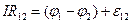, (6)
откуда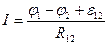 
. (7)
Формула (6) или (7) является математическим выражением обобщённого закона Ома для участка цепи электрического тока.
Если на данном участке цепи сторонние силы не действуют ( 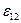=0), то из (7) приходим к закону Ома для однородного участка 
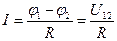. (8)
Итак, при отсутствии сторонних сил напряжение на концах участка цепи равно разности потенциалов.
Обобщённый закон Ома позволяет рассчитать практически любую сложную цепь. Однако непосредственный расчёт разветвлённых цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.), довольно сложен. Решение задачи значительно облегчается, если воспользоваться двумя правилами, сформулированными Кирхгофом.
Первое правило Кирхгофа : алгебраическая сумма токов, сходящихся в узле, равна нулю.
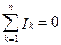, (9)
где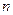 
- число проводников, сходящихся в узле;
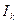- сила тока в 
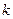-м проводнике, причём токи, подходящие к узлу, считаются положительными, а токи, отходящие от него, - отрицательными.
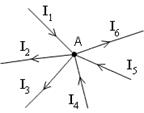Узлом называется любая точка разветвления цепи, в которой сходится не менее трёх проводников с током.
|
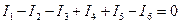
Следует отметить, что первое правило Кирхгофа вытекает из закона сохранения электрического заряда.
Второе правило Кирхгофа : в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма произведений сил токов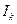 
на сопротивления 
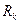соответствующих участков этого контура равна алгебраической сумме ЭДС 
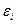, встречающихся в этом контуре:
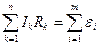, (10)
где 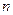- число участков, на которые контур разбивается узлами.
При составлении уравнений по второму правилу Кирхгофа необходимо условиться о направлении обхода контура (по часовой стрелке или против неё). Выбор этого направления совершенно произволен. Произведение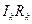 
входит в уравнение со знаком «плюс», если направление тока на данном участке совпадает с выбран-ным направлением обхода контура; в противном случае произведение 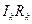берётся со знаком «минус».
ЭДС 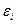источников тока, включённых на различных участках контура, считаются положительными, если они повышают потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от (-) к (+) внутри источника. В противном случае ЭДС входит в уравнение со знаком «минус».
4. Схема лабораторной установки, её описание.
Схема установки приведена на рис. 3. Она состоит из двух источников тока и набора резисторов, составляющих разветвлённую цепь. Величины сопротивлений указаны на лабораторном стенде.
|
|
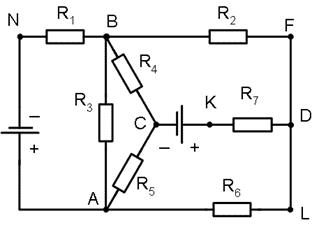
Рис. 3
Напряжение на каждом резисторе можно измерить вольтметром, к которому присоединяются проводники со щупами на концах.