Постановка задачи оптимального управления

Рассмотрим задачу оптимального управления:

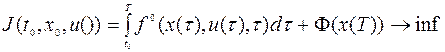, (9.1.1)

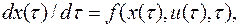
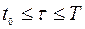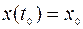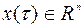, , , (9.1.2)

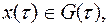
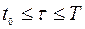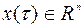, (9.1.3)

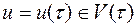, (9.1.4)

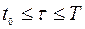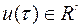, – кусочно–непрерывна

Моменты времени 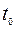, 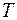будем считать заданными. Дифференциальные уравнения в (9.1.2) описывают движение некоторого управляемого объекта (течение управляемого процесса, изменения управляемой системы) в зависимости от времени t. Предполагается, что вектор 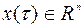(фазовые координаты) характеризует движение объекта (например, координаты объекта), а вектор 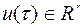характеризует управление объектом (например, «положения рулей» объекта) в момент времени t. Согласно (9.1.2), начальное состояние объекта определено 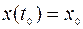. Если управление определено, то фазовые координаты объекта определяются как решение задачи Коши

, , .

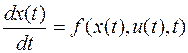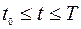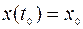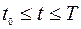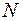Для приближенного решения задачи разобьем отрезок на частей точками 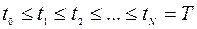и приняв эти точки в качестве узловых, заменим интеграл в (9.1.1) квадратурной формулой прямоугольников, уравнения (9.1.2) – разностными формулами с помощью явной схемы Эйлера. В результате придем к дискретной задаче оптимального управления:

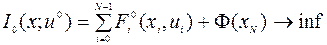, (9.1.5)

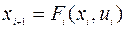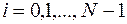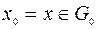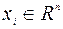, , , , (9.1.6)

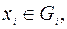
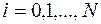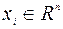, , (9.1.7)

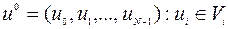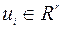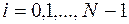, , , (9.1.8)

где 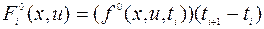, , 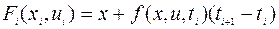, 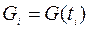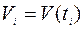. Задача (9.1.5)– (9.1.8) имеет самостоятельный интерес и возникает при описании управляемых дискретных систем, в которых сигналы управления поступают в дискретные моменты времени, фазовые координаты также меняются дискретно.

Система (9.1.6) с некоторым дискретным управлением 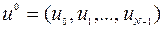однозначно определяет соответствующую дискретную траекторию 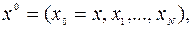обозначим ее 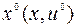. Зафиксируем некоторое 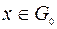и через 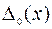обозначим множество управлений 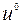таких, что 1) выполнены условия (9.1.8); 2) дискретная траектория , соответствующая управлению 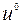и выбранному начальному условию 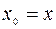, удовлетворяет ограничениям (9.1.7). Следовательно:

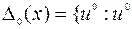удовлетворяет (9.1.8); траектория 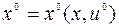удовлетворяет (9.1.7)}.

Пару (u⁰ , х⁰), состоящую из управления и траектории, будем называть допустимой для задачи (9.1.5)–(9.1.8), если эта пара удовлетворяет всем условиям (9.1.6)–( 9.1.8) или, иначе говоря, 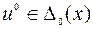. Если 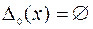при всех 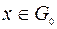, то условия (9.1.6)–

(9.1.8) несовместны и функция (9.1.5) будет определена на пустом множестве.

Обозначим

.

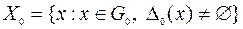Задача (9.1.5)–(9.1.8) формулируется кратко:

минимизировать 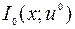при .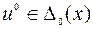

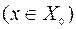Допустимую пару 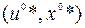назовем решением задачи (9.1.5)–(9.1.8), если

.

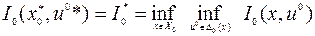Будем называть 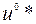– оптимальным управлением, 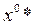– оптимальной траекторией задачи (9.1.5)–(9.1.8).

Задача (9.1.5)–(9.1.8) является задачей минимизации функции 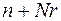переменных и для ее решения, в принципе, могут быть использованы методы нелинейного программирования (НЛП). Отмеченная размерность в практических задачах может быть очень высокой, а множества 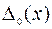, 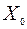заданы неявно, что сильно усложняет задачу НЛП.