Складання і дослідження канонічних рівнянь кривих другого порядку

Задача 43.1.Скласти рівняння еліпса, фокуси якого розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:

1) 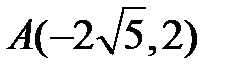–точка на еліпсі та 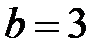– мала піввісь;

2) 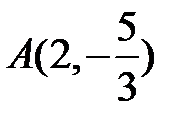– точка на еліпсі, 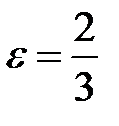– ексцентриситет.

Розв’язання.

1) Підставимо в канонічне рівняння еліпса замість 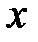та 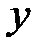координати точки А, а також дане значення 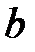. Одержимо рівняння: .

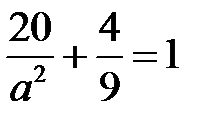Розв’яжемо його:

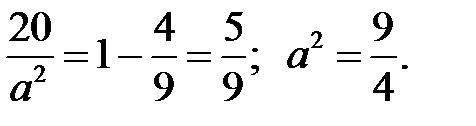
Отже, відповідь:

.

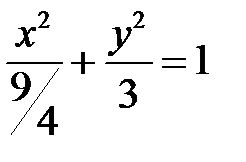1) З умови задачі маємо:

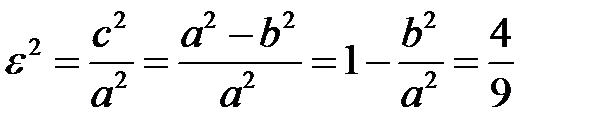, отже, .

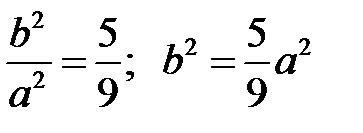З другого боку, підставимо у канонічне рівняння координати точки А. Одержимо систему рівнянь:

.

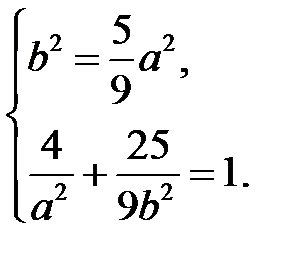Звідси

,

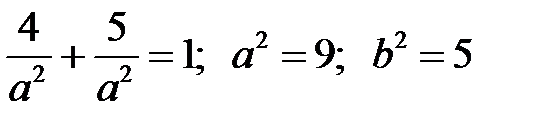отже шукане рівняння має вигляд:

.

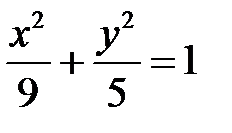Задача 43.2. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:

1) 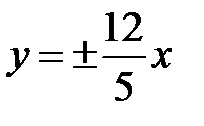– рівняння асимптот, 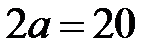– відстань між вершинами;

2) 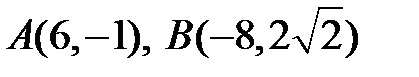– точки на гіперболі.