Интегральная формула уравнений Максвелла
На опыте измеряются величины, содержащиеся в интегральных характеристиках электромагнитного поля. Поэтому при решении некоторых задач удобнее перейти к интегральной формуле уравнений Максвелла.
Рассмотрим уравнение (2б) предыдущего параграфа. Проинтегрируем его по объему 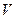
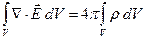 .
.
Учитывая, что 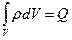 - суммарный заряд, сосредоточенный в объеме
- суммарный заряд, сосредоточенный в объеме 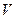 , и применяя теорему Гаусса к левой части, приходим к интегральной форме уравнения (2б):
, и применяя теорему Гаусса к левой части, приходим к интегральной форме уравнения (2б):
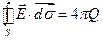 . (1) Здесь S - замкнутая поверхность, ограничивающая объём V. Поток вектора
. (1) Здесь S - замкнутая поверхность, ограничивающая объём V. Поток вектора 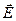 через некоторую поверхность S, не обязательно замкнутую, обозначают обычно
через некоторую поверхность S, не обязательно замкнутую, обозначают обычно 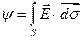 .
.
Соотношение (1) в теории электричества называется теоремой Гаусса.
Аналогичные выкладки применительно к уравнению (2б) предыдущего параграфа дают
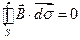 . (2)
. (2)
Поток вектора 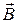 через некоторую поверхность
через некоторую поверхность 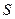 принято обозначать буквой
принято обозначать буквой 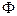 :
:
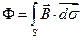 .
.
Пусть L - некоторый замкнутый контур, стягиваемый поверхностью S. Вычислим интеграл по поверхности S от левой и правой части (1а) предыдущего параграфа:
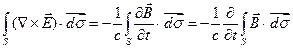 .
.
Применяя теорему Стокса к левой части этого соотношения, получим:
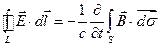 , (3)
, (3)
или
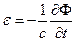 , (3а)
, (3а)
где через 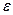 обозначена работа электрических сил, производимая полем над единичным точечным зарядом при перемещении его по конечному замкнутому контуру L. Величину
обозначена работа электрических сил, производимая полем над единичным точечным зарядом при перемещении его по конечному замкнутому контуру L. Величину 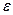 называют циркуляцией вектора
называют циркуляцией вектора 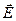 .
.
Уравнение (2а) предыдущего параграфа приводит к соотношению:
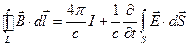 ,
,
где 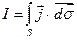 - полный ток через поверхность
- полный ток через поверхность 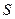 .
.
Т.о. система уравнений Максвелла для поля в вакууме в интегральной форме имеет вид:
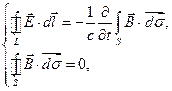 (5)
(5)
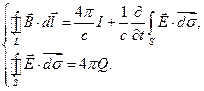 (6)
(6)
