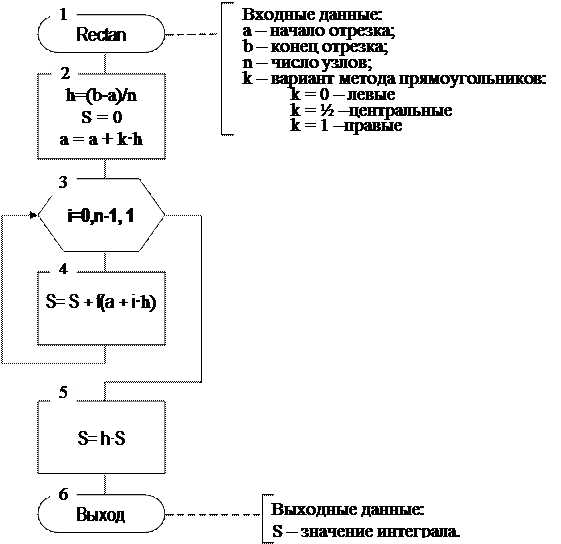
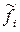Алгоритм решения ОДУ 1-го порядка методом Эйлера.

25.)

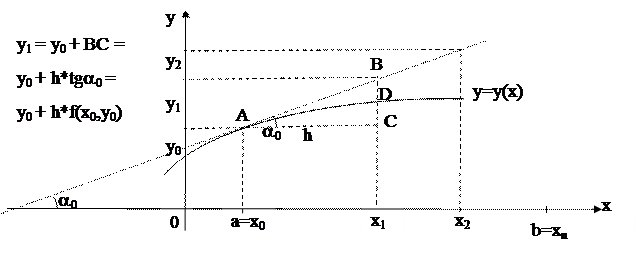Из геометрической иллюстрации следует, что:

1. На каждом шаге есть погрешность (на рисунке это отрезок BD). Погрешность тем больше, чем больше шаг.

2. Ошибка может накапливаться.

Формула Эйлера 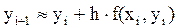имеет погрешность метода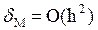

Для практического выбора h с целью обеспечения заданной точности решения задачи e применяется следующий прием.

Выполняются 2 расчета: с n и 2n узлами. Если полученные значения функции в во всех узлах отличаются не более чем на e, задача считается решенной. Если нет, число узлов вновь удваивают и опять сравнивают полученные значения функций.

Таким образом, расчет продолжается до достижения условия

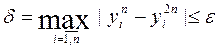
Порядок оценки погрешности метода Эйлера на одном шаге:

1)Записать разложение точного решения задачи Коши в точке 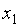по формуле Тейлора с остаточным членом в форме Лагранжа:

, .

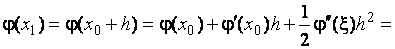
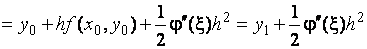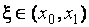2)Погрешность метода на одном шаге имеет порядок 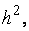так как

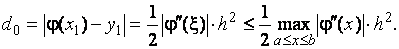
3)После 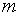шагов погрешность вычисления значения 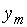в конечной точке отрезка возрастёт не более чем в 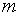раз. Погрешность метода Эйлера можно оценить неравенством

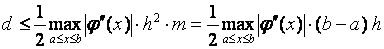
или представить в виде

,

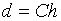где .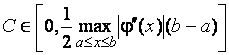

Метод Рунге-Кутта 4 порядка.

Метод Рунге-Кутта 4-го порядка- усреднение проводится по трём точкам, формула Эйлера на каждом отрезке используется 4 раза: в начале отрезка, дважды в его середине и в конце отрезка.

Расчетные формулы метода для дифференциального уравнения y^’ = f(x,y) имеют вид:

,

где i = 0, 1, …., n-1 - номер узла;

x_i = a + i×h - координата узла;

у₀ = у(х₀) - начальное условие.

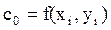
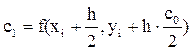
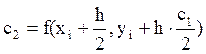
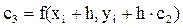
Погрешность метода d_М = О(h⁵).

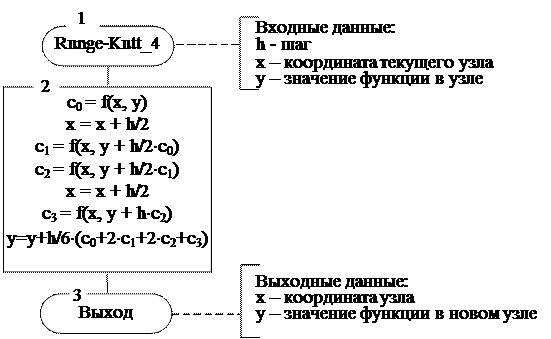
Схема алгоритма расчета новой точки методом Рунге-Кутта 4-го порядка.

26.)

Решение систем обыкновенных дифференциальных уравнений.

Системой дифференциальных уравнений называется система вида

где x - независимый аргумент, , где n – размерность системы.

y_i - зависимая функция, ,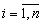

y_i|_x=x0 =y_i0 - начальные условия.

Функции y_i(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.

Решение системы дифференциальных уравнений методом Эйлера:

y_ij+1=y_ij+hf_i(x_i,y_1j y_2j..y_nj)

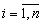
j - номер шага.

x_j+1=x_j+h

Модифицированный метод Эйлера.

k_i1=h*f_i(x_j,y_1j..y_nj)

k_i1=h*f_i(x_j+h,y_1j+k_i1..y_nj+k_i2)

y_ij+1=y_ij+(k_i1+k_i2)/2

x_j+1=x_j+h

Пусть задана система уравнений 1-го порядка:

y′ = f(x, y, z)

z′ = g(x, y, z)

с начальными условиями

y(x₀) = y₀ , z(x₀) = z₀ .

Приближенное решение системы определяется по формулам:

y_i+1 = y_i +∆y_i ,

z_i+1 = z_i + ∆z_i ,

где приращения ∆y_i и ∆z_i вычисляются в этом случае параллельно:

∆y_i = hf(x_i , y_i , z_i)

∆z_i = hg(x_i , y_i , z_i)

Формулы Эйлера-Коши для системы двух уравнений имеют следующий вид:

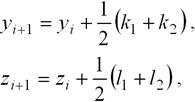
где

k₁ = hf(x_i , y_i , z_i),

l₁ = hg(x_i , y_i , z_i),

k₂ = hf(x_i+h, y_i+k₁ , z_i+l₁),

l₂ = hg(x_i+h, y_i+k₁ , z_i+l₁).

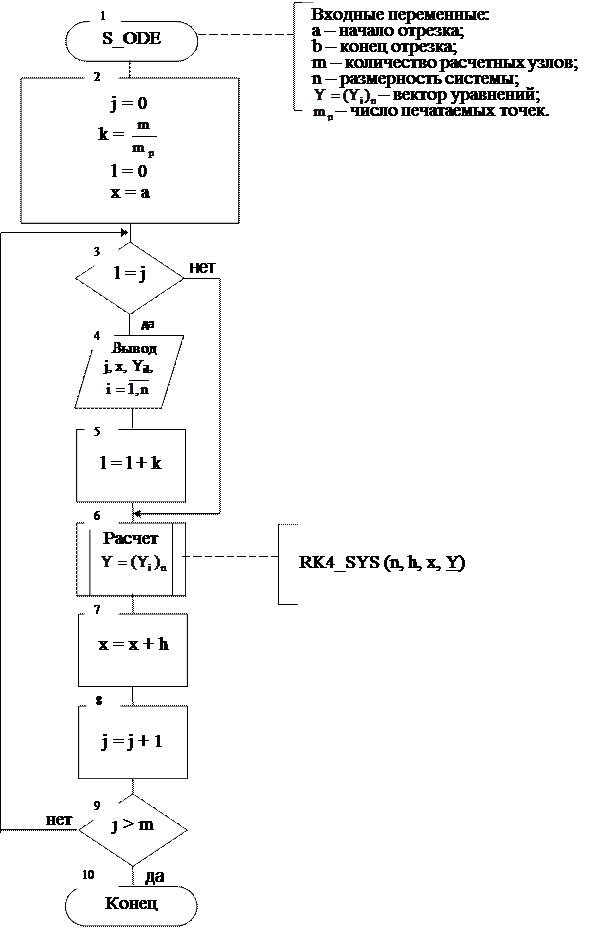
Алгоритм решения системы ОДУ.

27.)

Численное интегрирование — вычисление значения определённого интеграла.

Численное интегрирование применяется, когда:

1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .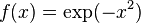

Если функция непрерывна на отрезке [a, b] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:

.

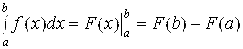Алгоритм получения определенного интеграла:

1)Сначала вычисляют значения функции f(x_i) = y_i в некоторых узлах x_i Î[a, b].

2)Затем выбирается интерполяционный многочлен P(x), проходящий через полученные точки (x_i, y_i), который используется при вычислении приближенного значения интеграла :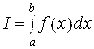

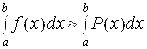
При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:

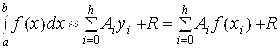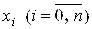,где - узлы интерполирования, A_i – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы.(квадратурная формула)

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b

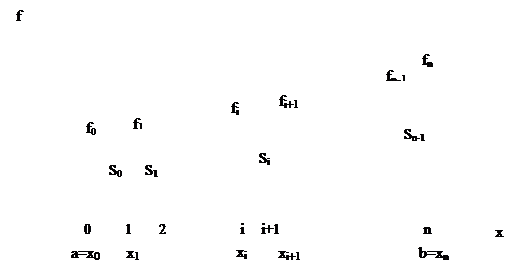
Отрезок [a, b] делят на n необязательно равных частей – элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x₀, x₁,…, x_n – узлами сетки.

Если сетка равномерная, то 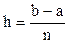– шаг сетки, при интегрировании – шаг интегрирования, а координата i-го узла вычисляется по формуле:

,

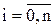
Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

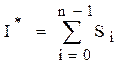
Квадратурные формулы отличаются друг от друга способом оценки значения S_i – площади элементарной криволинейной трапеции.

28.) Численное интегрирование — вычисление значения определённого интеграла.

Численное интегрирование применяется, когда:

1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .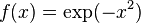

Если функция непрерывна на отрезке [a, b] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:

.

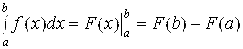Алгоритм получения определенного интеграла:

1)Сначала вычисляют значения функции f(x_i) = y_i в некоторых узлах x_i Î[a, b].

2)Затем выбирается интерполяционный многочлен P(x), проходящий через полученные точки (x_i, y_i), который используется при вычислении приближенного значения интеграла :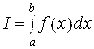

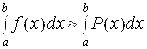
При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:

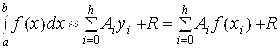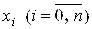,где - узлы интерполирования, A_i – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы.(квадратурная формула)

Метод прямоугольников.

Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами 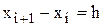и f_i. Тогда 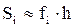и значение интеграла:

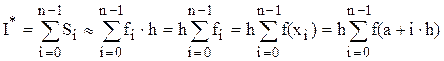
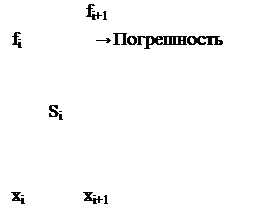
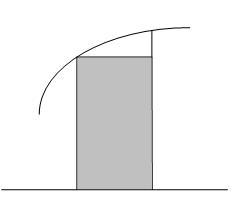
Оценка элементарной площади S_i левым прямоугольником.

Полученная формула называется формулой левых прямоугольников, т.к. для оценки площади использовалось левое основание элементарной криволинейной трапеции.

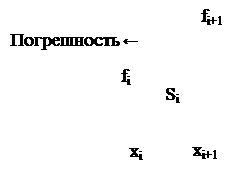Формула правых прямоугольников:

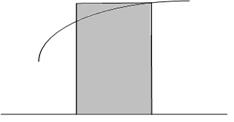
Оценка элементарной площади S_i правым прямоугольником.

Для данного случая 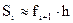и тогда значение интеграла:

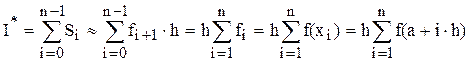
Эти формулы имеют большую погрешность, пропорциональную величине шага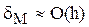

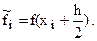
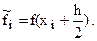
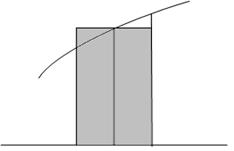
Для повышения точности площадь S_i можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка

Для повышения точности площадь S_i можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка

Оценка элементарной площади S_i центральным прямоугольником.

Для данного случая 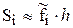и формула центральных прямоугольников имеет вид:

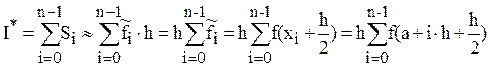
Погрешность в оценке площади S_i в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ₁ и δ₂).

Погрешность метода пропорциональная квадрату величины шага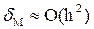

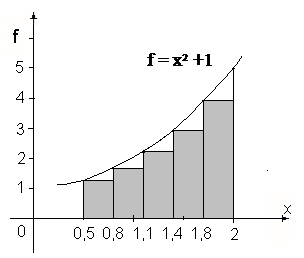Суммарная площадь

прямоугольников заметно

меньше площади

криволинейной трапеции.

Геометрическая иллюстрация вычисления значения определённого интеграла по формуле левых прямоугольников.