Уравнения Эйнштейна для внешнего фотоэффекта
Корпускулярные свойства света
Фотон
В природе существуют процессы, которые волновая оптика объяснить не может. При рассмотрении излучения черного тела Планку достаточно было предположить, что излучение происходит порциями (квантами). Однако, возникает вопрос: если излучение световых волн квантовано, то как же происходит поглощение и распространение света? Альберт Эйнштейн (1879-1955) предположил, что свет не только излучается, но и распространяется порциями. Причем каждая порция (квант) ведет себя как дискретная частица. Такие частицы были названы фотонами.
Непосредственное подтверждение гипотезы Эйнштейна дал опыт Вальтера Боте (1891–1957). Тонкая фольга помещалась между двумя регистрирующими устройствами. Фольга облучалась слабым пучком рентгеновских лучей. От регистрирующих устройств импульс передавался на особый механизм, делавший отметки на движущейся ленте. Если бы энергия распространялась по всем направлениям равномерно, то оба счетчика срабатывали бы одновременно. Однако, отметки на ленте были не одна против другой, а располагались беспорядочно.
В основе квантовой теории света лежит формула, связывающая энергию фотона и частоту колебаний световой волны
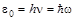 . (8.1.1)
. (8.1.1)
Эта формула, с учетом соотношения между энергией и массой 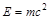 , позволяет определить массу фотона
, позволяет определить массу фотона
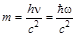 . (8.1.2)
. (8.1.2)
Принято говорить, что фотон не имеет массы покоя, а обладает только массой движения. Такое понимание массы фотона, вообще говоря, лишено всякого смысла, поскольку фотонов без поступательного движения вообще не существует. Наличие у фотона массы позволяет сделать предположение о том, что фотон можно, как и другие частицы, характеризовать импульсом. В соответствии с общими представлениями об импульсе можно записать
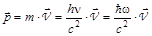 , (8.1.3)
, (8.1.3)
где 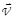 – скорость фотона. Учитывая модуль скорости света
– скорость фотона. Учитывая модуль скорости света 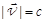 , получим следующее выражение для модуля импульса фотона
, получим следующее выражение для модуля импульса фотона
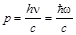 . (8.1.4)
. (8.1.4)
Используя выражение для волнового вектора 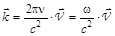 , выражение для импульса фотона принимает вид
, выражение для импульса фотона принимает вид
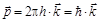 . (8.1.5)
. (8.1.5)
Все приведенные величины связаны с волновыми характеристиками излучения – частотой, длиной волны и волновым вектором. Поэтому возникает естественный вопрос: существует ли величина, характеризующая фотон и не зависящая от волновых характеристик. Такой величиной является собственный момент импульса или спин. Он находится из сравнения момента вращения, создаваемого световой волной, с суммарным моментом количества движения фотонов, содержащихся в световом потоке. Единичная площадка поверхности тела получит от волны за одну секунду энергию, равную модулю вектора Умова-Пойтинга 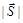 . Тогда,
. Тогда,
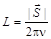 .
.
С другой стороны, 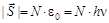 , где N – количество фотонов в потоке. Следовательно,
, где N – количество фотонов в потоке. Следовательно,
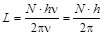 .
.
Суммарный момент количества движения потока фотонов складывается из спинов всех фотонов, то есть L = N×l, где l – спин одного фотона. Таким образом
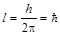 . (8.1.6)
. (8.1.6)
Остается выяснить, имеет ли фотон заряд. В этом легко убедиться. Рассматривая свет как поток заряженных частиц и используя закон сохранения заряда, мы приходим к выводу, что любая поверхность зарядилась бы в результате падения на него света. Однако, опыт убеждает нас в обратном. Опыт также показывает, что фотоны не имеют электрического дипольного момента, магнитного момента, а время жизни фотона без взаимодействия с веществом следует считать бесконечным.
Внешний фотоэффект
Одним из явлений, подтверждающих гипотезу о существовании фотонов, является фотоэлектрический эффект (коротко фотоэффект). Впервые фотоэффект наблюдал Генрих Герц (1857-1894). Он обнаружил, что при освещении ультрафиолетовым светом отрицательного электрода, находящегося под напряжением, наблюдается проскакивание искры между электродами. Сущность явления, обнаруженного Герцем, состоит в том, что при освещении ультрафиолетовыми лучами отрицательно заряженного металлического тела, оно теряет отрицательный заряд (фотоэлектронная эмиссия или внешний фотоэффект). При освещении такими же лучами положительно заряженного тела, потеря заряда не наблюдается, из чего следует вывод, что теряются электроны.
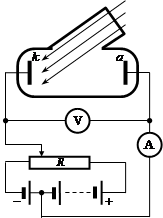 Внешний фотоэффект, открытый Герцем, состоит в вырывании электронов из поверхностного слоя вещества. Внешний фотоэффект сильно зависит от состояния поверхности вещества. Кроме того, чтобы получить однозначные результаты при исследовании фотоэффекта, опыты лучше производить в хорошем вакууме. Электроны, вырванные под действием света, называются фотоэлектронами. Фотоэлектрическими свойствами обладают как металлы, так и диэлектрики, полупроводники и электролиты. Первым систематически исследовал фотоэффект Александр Григорьевич Столетов (1839—1896). Принципиальная схема экспериментов для изучения фотоэффекта состоит из вакуумной двухэлектродной лампы, источника постоянного тока, переменного сопротивления, амперметра и вольтметра. На основе проведенных исследований Столетов пришел к следующим выводам:
Внешний фотоэффект, открытый Герцем, состоит в вырывании электронов из поверхностного слоя вещества. Внешний фотоэффект сильно зависит от состояния поверхности вещества. Кроме того, чтобы получить однозначные результаты при исследовании фотоэффекта, опыты лучше производить в хорошем вакууме. Электроны, вырванные под действием света, называются фотоэлектронами. Фотоэлектрическими свойствами обладают как металлы, так и диэлектрики, полупроводники и электролиты. Первым систематически исследовал фотоэффект Александр Григорьевич Столетов (1839—1896). Принципиальная схема экспериментов для изучения фотоэффекта состоит из вакуумной двухэлектродной лампы, источника постоянного тока, переменного сопротивления, амперметра и вольтметра. На основе проведенных исследований Столетов пришел к следующим выводам:
- наибольшее действие оказывают ультрафиолетовые лучи;
- сила тока на амперметре возрастает с увеличением освещенности пластины;
- испускаемые под действием света заряды имеют отрицательный знак.
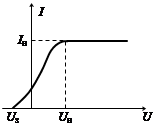 Если при постоянной интенсивности света и частоте падающего света увеличивать напряжение между анодом и катодом, то сила фототока перестает расти после некоторого значения напряжения Uн. Значение Iн, соответствующее Uн, называют током насыщения. Насыщение достигается тогда, когда все электроны, вырванные в единицу времени с поверхности катода, достигают анода за единицу времени. При некотором значении напряжения Uз, фототок совсем исчезает. При этом значении разности потенциалов энергии, сообщенной электронам, не хватает, чтобы покинуть катод и долететь до анода. Uз – называют задерживающим напряжением.
Если при постоянной интенсивности света и частоте падающего света увеличивать напряжение между анодом и катодом, то сила фототока перестает расти после некоторого значения напряжения Uн. Значение Iн, соответствующее Uн, называют током насыщения. Насыщение достигается тогда, когда все электроны, вырванные в единицу времени с поверхности катода, достигают анода за единицу времени. При некотором значении напряжения Uз, фототок совсем исчезает. При этом значении разности потенциалов энергии, сообщенной электронам, не хватает, чтобы покинуть катод и долететь до анода. Uз – называют задерживающим напряжением.
Уравнения Эйнштейна для внешнего фотоэффекта
Можно было бы попытаться дать качественное объяснение фотоэффекта с волновой точки зрения. Свободные электроны, имеющиеся в металле, удерживаются в нем задерживающим полем атомов. Работа, которую нужно совершить, чтобы вывести электрон из металла, составляет несколько электрон-вольт. В электромагнитном поле световой волны электрон приходит в колебательное движение. Когда энергия колебаний сделается достаточно большой, электрон может преодолеть задерживающее поле и покинуть металл. Если же электрон связан, то все будет происходить аналогично.
Однако, такое объяснение не согласуется с опытом. Во-первых, кинетическая энергия электрона должна быть тем больше, чем больше интенсивность падающего света. Но опыты показали, что максимальная скорость фотоэлектронов определяется только частотой падающего света. Во-вторых, по классической волновой теории фотоэффект должен происходить с запаздыванием, так как для накопления энергии колебаний требуется определенное время. Но опыт показывает, что фототок появляется одновременно с появлением света.
Корпускулярная теория света устраняет трудности при описании фотоэффекта. Согласно ей при столкновении фотона и электрона фотон отдает всю энергию электрону и прекращает свое существование. Другими словами, электрон приобретает энергию в результате единичного акта столкновения. Энергия, полученная электроном, может расходоваться на отрыв электрона от атома и выход электрона из вещества. Если при этом электрон был свободным, а при вылете не сталкивался с другими частицами вещества и не расходовал энергию на тепло, то энергия электрона тратилась только на преодоление задерживающих сил. Минимальную энергию, которая требуется электрону для выхода из металла, называют работой выхода. Из закона сохранения энергии следует
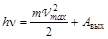 . (8.3.1)
. (8.3.1)
где Авых – работа выхода, а первое слагаемое в правой части равенства характеризует кинетическую энергию электрона, которая в данном случае будем максимальной. Эта формула носит название формулы Эйнштейна.
Из формулы Эйнштейна вытекает несколько следствий, находящихся в строгом согласии с опытом и названных законами внешнего фотоэффекта или законами Столетова:
- максимальная кинетическая энергия электронов зависит от частоты падающего света и не зависит от его интенсивности;
- интенсивность света оказывает влияние только на количество вырванных электронов, но не влияет на максимальную кинетическую энергию фотоэлектрона;
- существует минимальная частота падающего света, при которой фотоэффект еще наблюдается (красная граница фотоэффекта).
Первые два следствия элементарно объясняются корпускулярной теорией света. Так как фотон поглощается электроном в результате единичного акта столкновения, и вероятность столкновения одного и того же электрона с другим фотоном мала, то энергия, полученная электроном, зависит от энергии падающих на катод фотонов, то есть от их частоты. По той же самой причине количество выбитых фотоэлектронов пропорционально плотности фотонного потока, то есть интенсивности света. Что касается третьего следствия, то достаточно предположить, что существует такая частота n0, при которой энергия падающих фотонов равняется энергии выхода электронов из катода 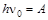 . Если
. Если 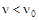 , то
, то 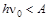 , то есть энергии, полученной электроном от фотона, недостаточно, для того чтобы преодолеть притяжение ионного остова катода.
, то есть энергии, полученной электроном от фотона, недостаточно, для того чтобы преодолеть притяжение ионного остова катода.
Фотоэффект нашел свое применение в технике. Одно из них состоит в получении рентгеновских лучей при обратном фотоэффекте. Для рентгеновских лучей энергия светового кванта hn велика по сравнению с работой выхода A. В этом случае величиной A в формуле Эйнштейна можно пренебречь
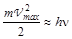 . (8.3.2)
. (8.3.2)
Практически процесс получения рентгеновских лучей таков: между электродами вакуумной лампы создают разность потенциалов U. В результате термоэлектронной эмиссии электроны покидают катод и направляются к аноду. При попадании на анод электроны тормозятся полем материала анода и излучают энергию в виде квантов. Энергия фотонов, а, следовательно, и частота рентгеновских лучей пропорциональна разгоняющей разности потенциалов
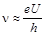 . (8.3.3)
. (8.3.3)
Внутренний фотоэффект
Во внешнем фотоэффекте энергия фотона передается свободным электронам, после чего они покидают поверхность проводника. Однако, существует вероятность столкновения фотонов с валентными электронами вещества. Если энергии фотона достаточно для преодоления электроном запрещенной зоны, то он становится электроном проводимости. Увеличение количества свободных электронов внутри твердого тела приводит к увеличению его проводимости. Это явление получило название внутренний фотоэффект.
Внутренний фотоэффект широко используется в различных регистрирующих устройствах. Обычно в таких устройствах используются, так называемые, светодиодные пары. Светодиодная пара состоит из излучателя и приемника (фотодиода). Излучатель посылает световой сигнал к фотодиоду, включенному в электрическую цепь сигнального устройства. При изменении освещенности фотодиодного датчика изменяется и его сопротивление, что, в свою очередь, приводит к изменению тока в цепи сигнального устройства.
Перераспределение электронов по энергетическим уровням приводит к изменению внутреннего электрического поля в кристалле. Это ведет к появлению ЭДС на границе двух различных полупроводников или полупроводника и металла. Данное явление получило название вентильного фотоэффекта. По сути, механизм вентильного фотоэффекта ничем не отличается от внутреннего. Как известно, причина односторонней проводимости p-n-перехода заключается в существовании двойного запирающего слоя на границе контакта двух полупроводников. В процессе облучения этого запирающего слоя количество электронов в нем увеличивается, что приводит к возникновению контактной разности потенциалов. Для того чтобы фотоны могли достигнуть запирающего слоя, на поверхность полупроводника n-типа наносят тонкий слой полупроводника p-типа и через эту тонкую пленку облучают p-n-переход.
 8.5 Комптоновское рассеяние
8.5 Комптоновское рассеяние
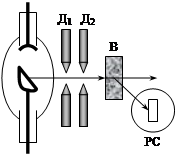 В 1922 году Артур Комптон (1892-1962) открыл явление, которое, как и фотоэффект, связано с корпускулярными свойствами света. Комптон изучал рассеяние жесткого рентгеновского излучения на телах, состоящих из легких атомов. При этом он обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны l, содержатся также лучи большей длины волны l¢. Разность длин волн Dl=l¢-l оказалась зависящей только от угла рассеяния. Изменение длины волны получило название комптоновского смещения, а само явление – эффект Комптона. Схема опытов Комптона представлена на рисунке. Узкий пучок рентгеновских лучей, выделяемый диафрагмами Д1 и Д2, рассеивается веществом (В) с легкими атомами (углерод, парафин и т.д.). Рассеянный свет изучается на рентгеновском спектрографе (РС).
В 1922 году Артур Комптон (1892-1962) открыл явление, которое, как и фотоэффект, связано с корпускулярными свойствами света. Комптон изучал рассеяние жесткого рентгеновского излучения на телах, состоящих из легких атомов. При этом он обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны l, содержатся также лучи большей длины волны l¢. Разность длин волн Dl=l¢-l оказалась зависящей только от угла рассеяния. Изменение длины волны получило название комптоновского смещения, а само явление – эффект Комптона. Схема опытов Комптона представлена на рисунке. Узкий пучок рентгеновских лучей, выделяемый диафрагмами Д1 и Д2, рассеивается веществом (В) с легкими атомами (углерод, парафин и т.д.). Рассеянный свет изучается на рентгеновском спектрографе (РС).
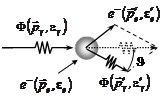 С точки зрения волновой теории, возникновение излучения с длиной волны l¢ невозможно. Однако, такое изменение не вызывает непонимания, если рассматривать его с корпускулярной точки зрения. Рассмотрим упругое столкновение свободного электрона
С точки зрения волновой теории, возникновение излучения с длиной волны l¢ невозможно. Однако, такое изменение не вызывает непонимания, если рассматривать его с корпускулярной точки зрения. Рассмотрим упругое столкновение свободного электрона 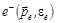 с рентгеновским фотоном
с рентгеновским фотоном 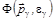 . При этом будем предполагать, что электрон покоится. Такое предположение обосновано тем, что скорость движения электронов в веществе мала по сравнению со скоростью света. Энергия и импульс фотона до и после столкновения имеют вид:
. При этом будем предполагать, что электрон покоится. Такое предположение обосновано тем, что скорость движения электронов в веществе мала по сравнению со скоростью света. Энергия и импульс фотона до и после столкновения имеют вид: 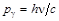 ,
, 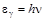 и
и 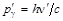 ,
, 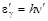 . Энергия и импульс электрона до и после столкновения соответственно:
. Энергия и импульс электрона до и после столкновения соответственно: 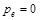 ,
, 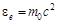 и
и 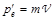 ,
, 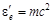 . Согласно законам сохранения энергии и импульса
. Согласно законам сохранения энергии и импульса
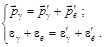 или
или 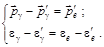 (8.5.1)
(8.5.1)
В законе сохранения импульса необходимо избавиться от векторов. Из рисунка (стр. 114) видно, что 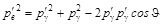 . Тогда система уравнений примет вид
. Тогда система уравнений примет вид
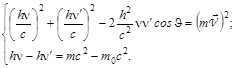 (8.5.2)
(8.5.2)
Возведем второе уравнение системы (8.5.2) в квадрат и поделим на с2
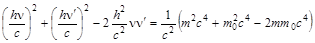 . (8.5.3)
. (8.5.3)
Вычтем из полученного уравнения (8.5.3) первое уравнение системы (8.5.2)
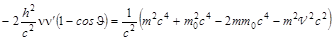 .
.
Воспользуемся преобразованиями специальной теории относительности, из которой следует, что 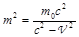 . Тогда,
. Тогда,
 ,
,
следовательно,
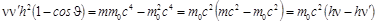 .
.
Поделив это уравнение на h, получим
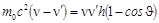 .
.
Таким образом, полученное выражение определяет зависимость изменения частоты световой волны при рассеянии на электронах. Однако, удобнее выражать изменение не частоты, а длины волны (  ,
, 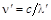 )
)
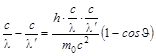 или
или 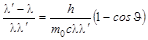 ;
;
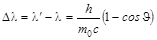 . (8.5.4)
. (8.5.4)
Величину 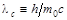 называют комптоновской длиной волны, а уравнение (8.5.4) принимает вид
называют комптоновской длиной волны, а уравнение (8.5.4) принимает вид
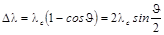 . (8.5.5)
. (8.5.5)
Формула (8.5.5) показывает, что рассеяние фотонов на неподвижных свободных электронах должно всегда сопровождаться увеличением длины волны. Однако, кроме этого происходит рассеяние без изменения длины волны. Это происходит, когда фотон рассеивается на связанных электронах. В этом случае импульс и энергия передаются всему атому. Вследствие того, что масса атома велика, lс будет мала, а с ней и Dl будет очень маленькой.
Чем больше энергия налетающего фотона, тем в меньшей степени проявляется связь электрона с ядром. Вот почему для эффекта Комптона необходимо использовать жесткие рентгеновские лучи. Однако, когда 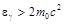 , при взаимодействии его с веществом начинается процесс образования электрон-позитронных пар. Отметим также, что рассеяние фотонов на атомах когерентно, а на свободных электронах некогерентно. Это очевидно, поскольку свободные электроны и их движения независимы, а связанные согласованы между собой.
, при взаимодействии его с веществом начинается процесс образования электрон-позитронных пар. Отметим также, что рассеяние фотонов на атомах когерентно, а на свободных электронах некогерентно. Это очевидно, поскольку свободные электроны и их движения независимы, а связанные согласованы между собой.
Давление света
Как любая частица, фотон при взаимодействии с некоторой поверхностью должен обмениваться с ней не только энергией, но и импульсом, то есть оказывать на нее давление. Световое давление было впервые обнаружено экспериментально и измерено Петром Николаевичем Лебедевым (1866-1912). Прибор Лебедева состоял из легкого подвеса на тонкой нити, по краям которого были прикреплены тонкие и легкие лепестки. Один из них был зачернен, а другой оставлен блестящим. Подвес помещался в сосуд, из которого откачивали воздух. Таким образом, получались очень чувствительные крутильные весы. Свет от дуговой лампы с помощью системы линз и зеркал концентрировался на одном из лепестков и вызывал закручивание подвеса. О давлении света можно было судить по величине закручивания подвеса.
Главными трудностями в опытах Лебедева являлись действие конвекционных потоков и наличие радиометрического действия. Данные помехи могут в сотни раз превосходить действие света. Конвекционные потоки закручивают подвес, если лепестки расположены не вертикально, а несколько наклонены. Так как действие конвекционных потоков не зависит от направления падающего света, то Лебедев исключал его с помощью изменения направления освещенности. Радиометрическое действие возникает в разреженном газе вследствие разности температур освещенной и неосвещенной сторон лепестка. Молекулы газа отражаются от более теплой стороны с большей скоростью, и крутильные весы поворачиваются в том же направлении, что и под действием светового давления. Радиометрическое действие можно уменьшить, используя очень тонкие металлические лепестки, а также создавая более высокий вакуум. Когда свет направлен на блестящий лепесток, то он вызывает большее закручивание подвеса. Радиометрическое действие наоборот, больше при освещении зачерненного лепестка, так как происходит больший нагрев облучаемой поверхности.
В рамках фотонной теории давление света можно интерпретировать как результат передачи импульса фотонов освещенной поверхности. Если поток монохроматического света, падающий на единицу поверхности тела в единицу времени, несет энергию равную W и содержит N фотонов, то
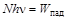 . (8.6.1)
. (8.6.1)
Если коэффициент отражения поверхности равен R, то 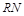 фотонов отражается, а
фотонов отражается, а 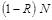 фотонов поглощается. При поглощении фотона поверхность приобретает энергию, равную энергии фотона и его импульс. Нормальная составляющая переданного импульса равна
фотонов поглощается. При поглощении фотона поверхность приобретает энергию, равную энергии фотона и его импульс. Нормальная составляющая переданного импульса равна 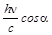 , где a – угол между направлением движения фотона и нормалью к поверхности. В случае, когда налетающий фотон испытывает упругое столкновении с поверхностью, он передает ей вдвое больший импульс. Тогда, полный импульс, переданный единице поверхности в единицу времени, равен
, где a – угол между направлением движения фотона и нормалью к поверхности. В случае, когда налетающий фотон испытывает упругое столкновении с поверхностью, он передает ей вдвое больший импульс. Тогда, полный импульс, переданный единице поверхности в единицу времени, равен
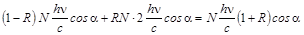 .
.
Так как импульс, переданный единице поверхности в единицу времени, не что иное, как давление, оказываемое на поверхность, то, с учетом соотношения (8.6.1), получим
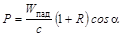 . (8.6.2)
. (8.6.2)
В случае нормального падения света ( 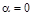 ), выражение для давления принимает наиболее простой вид
), выражение для давления принимает наиболее простой вид
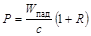 . (8.6.3)
. (8.6.3)
Такое же выражение для давления света было получено Максвеллом в рамках волновой теории. Рассуждения Максвелла сводились к следующему. Так как свет есть электромагнитная волна, то, падая на поверхность проводника, электрический вектор, лежащий в плоскости освещенной поверхности, вызывает электрический ток. Этот ток направлен так же, как и вектор напряженности электрического поля. Магнитное поле действует на данный ток по закону Ампера. При этом направление действия данной силы совпадает с направлением распространения волны. Такое действие и вызывает давление на поверхность. Сила давления зависит от интенсивности света. Для случая, когда лучи образуют параллельный пучок, падающий на абсолютно черное тело, давление равняется плотности световой энергии, то есть энергии в единице объема.
