Применение дифференциала к приближенным вычислениям

1 В приближенных вычислениях встречаются понятия абсолютной и относительной погрешностей.

Абсолютной погрешностью приближенной величины 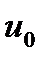называется абсолютная величина разности между точным значением 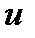этой величины и ее приближением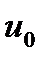

.

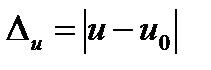Чаще 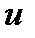и, следовательно, 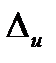неизвестны. Вводят понятие.

Границей абсолютной погрешности приближенной величины 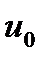называется любое число 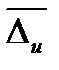, не меньшее абсолютной погрешности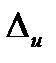

,

.

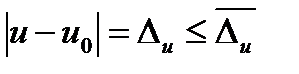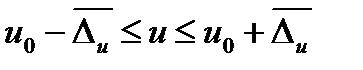Чем меньше 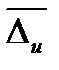, тем точнее найдена 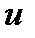. Зная границу погрешности, еще нельзя судить о качестве приближения.

Относительной погрешностью называется отношение 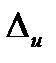и модуля приближенного значения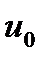

.

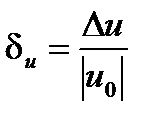Границей относительной погрешности 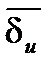называется

.

Относительная погрешность 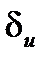и ее граница 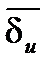выражаются в процентах.

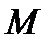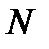Пример. Расстояние от точки до известно с точностью до 1 км, 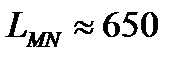км. Длина человека известна с точностью до 10 см, 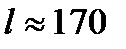см. Определить границы относительной погрешности этих измерений.

Решение.

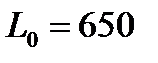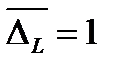км, км,

;

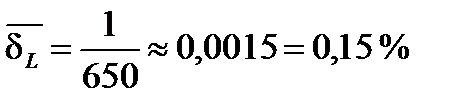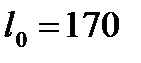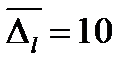см, см,

.

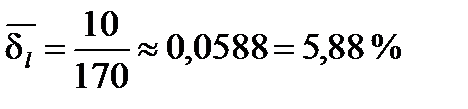Таким образом, измерение 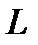точнее, чем .

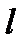2 Пусть известно значение 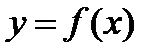и ее производная в точке 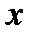. Покажем, как найти 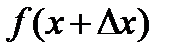в некоторой близкой точке .

,

,

,

,

.

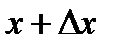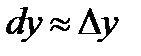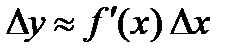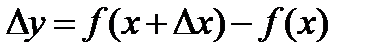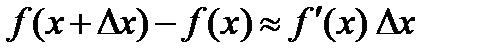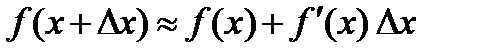Абсолютная погрешность не превышает ,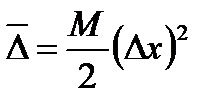

где 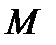– наибольшее значение 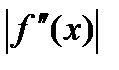на .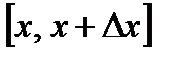

Пример. Найти .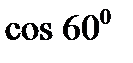

Решение.

,

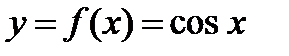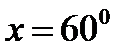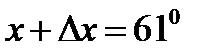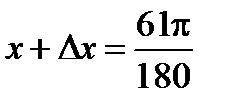, , (в радианах), ;

,

,

.

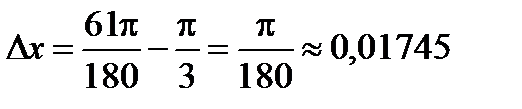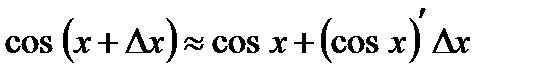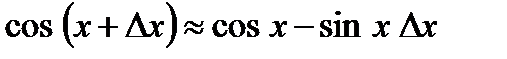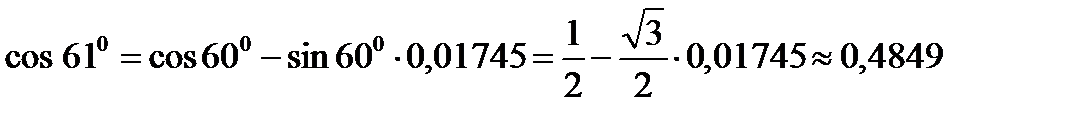3 Дифференциалы применяются при оценке погрешности.

Пусть величины 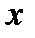и 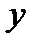связаны функцией 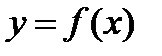и известно приближенное значение 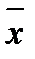величины 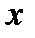с предельной абсолютной погрешностью 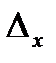. Следовательно, в качестве приближенного значения получим 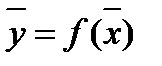. Для подсчета предельной абсолютной погрешности 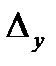заметим, что

, ,

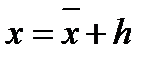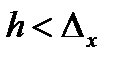следовательно, если 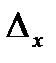мало, то 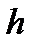мало и

,

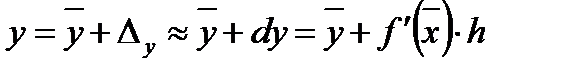то есть

,

.
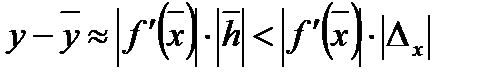
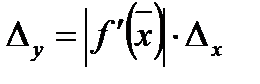