Запис додатних раціональних чисел у вигляді десяткових дробів
Означення. Десятковим дробом називається дріб, знаменником якого є 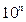 , де п Є N, і який записано в позиційній десятковій системі числення так: записано чисельник і в ньому справа наліво відділено п цифр (десяткових знаків).
, де п Є N, і який записано в позиційній десятковій системі числення так: записано чисельник і в ньому справа наліво відділено п цифр (десяткових знаків).
Наприклад. 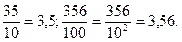
Якщо число цифр чисельника не більше від показника п (тобто не більше, ніж кількість нулів у степені десяти, що є знаменником), то зліва дописують необхідну кількість нулів.
Наприклад. 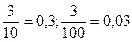 і т. д.
і т. д.
Зазвичай, десяткові дроби значно більше застосовують при обчисленні, ніж звичайні. Це пояснюється ще й тим, що в основу метричної системи мір також взято число 10, а тому при практичних вимірюваннях здебільшого дістаємо десяткові дроби. Через те тепер у школі після першого ознайомлення із звичайними дробами спочатку вивчають дії над десятковими дробами, а потім над звичайними.
Основна властивість десяткового дробу:
дописування нулів справа дробової частини запису десяткового дробу не змінює його значення.
Наприклад, 0,3 = 0,30 = 0,300 = ..., що випливає з основної властивості звичайних дробів:
Будь-яке натуральне число атат-1... 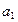 можна подати у вигляді десяткового дробу атат-1...
можна подати у вигляді десяткового дробу атат-1... 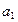 , 0 ...0.
, 0 ...0.
При перенесенні у десятковому дробові коми на і цифр праворуч значення дробу збільшується в 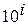 разів, а ліворуч — зменшується в
разів, а ліворуч — зменшується в 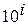 разів. Це випливає з самого означення десяткового дробу.
разів. Це випливає з самого означення десяткового дробу.
Правило. Щоб даний десятковий дріб помножити або поділити на 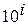 , треба перенести кому на і цифр відповідно вправо або вліво.
, треба перенести кому на і цифр відповідно вправо або вліво.
Оскільки у дробовій частині запису десяткових дробів можна справа дописувати нулі, від чого значення дробу не змінюється, то в загальному вигляді два десяткових дроби можна записати так, що вони матимуть однакову кількість цифр після коми, тобто будуть зведені до спільного знаменника.
Наприклад, щоб порівняти десяткові дроби 12,34 і 6,36472, перший дріб можна записати так: 12,34000, і тоді порівняння десяткових дробів можна звести до порівняння їх чисельників. Проте практично для порівняння десяткових дробів дописувати нулі немає потреби. Досить порівняти цілі частини; той дріб виражає більше число, у якого ціла частина більша. Якщо цілі частини рівні, той дріб виражає більше число, у якого більше десятих часток, і т. д.
Правило. Десяткові дроби слід додавати, як натуральні числа, не звертаючи уваги на коми, тільки всі розряди слід підписувати під відповідними їм розрядами, і в одержаній сумі відокремити справа стільки десяткових знаків, скільки їх має доданок з найбільшою кількістю десяткових знаків.
Примітка. Тут сказано «з найбільшою кількістю десяткових знаків», а не «стільки десяткових знаків, скільки їх має кожний доданок» тому, що практично нулі у десятковій частині не дописують, а просто їх мають на увазі.
Наприклад. + 23,516
982,8
1006,316
Закони додавання, доведені для звичайних дробів, мають місце і для десяткових дробів, оскільки десяткові дроби є окремим випадком звичайних.
Віднімання виконується аналогічно:
Наприклад. 415,634
¯ 12,78
402,854
Правило.Десяткові дроби слід перемножати, як натуральні числа, не звертаючи уваги на коми, а потім відокремити в добутку стільки десяткових знаків, скільки їх у множеному і множнику разом.
Наприклад. 12,36
Х 1,214
+ 4944
1236____
15,00504
Для десяткових дробів зберігаються перевірені уже для звичайних дробів закони множення.
Як показано вище, в результаті виконання дій додавання, віднімання і множення над десятковими дробами завжди дістаємо десяткові дроби.
Розглянемо ділення десяткового дробу на десятковий дріб.
Наприклад,
1) 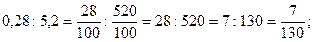
2) 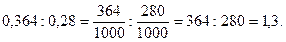
Як уже зазначалось, будь-яке ціле число можна записати у вигляді десяткового дробу, з нулями після коми.
Наприклад, 5 = 5,000...
Виникає запитання: чи будь-яке дробове число можна зобразити у вигляді десяткового дробу? Щоб дати відповідь на це запитання, проаналізуємо, за якою ознакою приклади записано у правій і у лівій колонках?
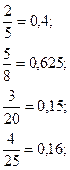
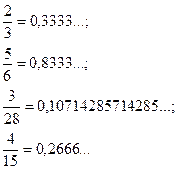
Відповідні дробові числа правої і лівої колонок мають однакові чисельники, проте залежно від знаменників або процес ділення чисельника на знаменник закінчується і в результаті дістаємо скінченний десятковий дріб (зліва), або не закінчується і дістаємо нескінченний десятковий дріб (справа), причому обов’язково періодичний — у ньому одна або кілька цифр періодично повторюються. При уважному аналізі можна помітити, чим відрізняються знаменники дробів правої і лівої колонок.
Теорема 1. Для того щоб звичайний нескоротний дріб можна було перетворити у десятковий, необхідно й достатньо, щоб канонічний розклад його знаменника не містив жодних простих множників, крім 2 і 5.
Наслідок. Будь-який нескоротний дріб, канонічний розклад знаменника якого не містить ніяких множників, крім 2 і 5, можна подати у вигляді десяткового дробу, причому двома способами:
1) діленням його чисельника на знаменник;
2) домноженням чисельника і знаменника дробу на відповідний степінь 2 або 5.
Приклади.
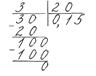 1)
1) 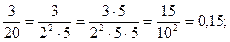 або
або
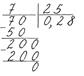 2)
2) 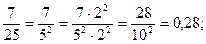 або
або
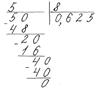 3)
3) 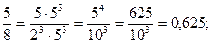 або
або
Теорема 2. Якщо нескоротний дріб — не перетворюється у скінченний десятковий, то його можна записати у вигляді нескінченного десяткового періодичного дробу (такий десятковий запис дробу, у якому, починаючи з деякого місця, одна і та сама цифра або сукупність цифр без кінця повторюються в певному порядку).
Сукупність цифр, які повторюються, називається періодом. У періоді буде не більше ніж п — 1 цифра. Наприклад,
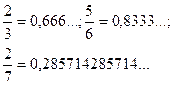
Розрізняють чисті і мішані періодичні десяткові дроби.
Чистим періодичним десятковим дробом називається періодичний десятковий дріб, у якого період починається безпосередньо після коми: 0,333..., 0,232323...
Мішаним періодичним десятковим дробом називається періодичний десятковий дріб, у якого період починається не відразу після коми: 0,08333..., 17,12777... При цьому число, що стоїть між комою і початком періоду, називається доперіодичною частиною.
Періодичні десяткові дроби записують компактніше, беручи період у дужки:
0,232323…= 0,(23) – нуль цілих і 23 в періоді;
0,08333… = 0,08(3) – нуль цілих, нуль вісім до періоду і 3 в періоді.
Чистий періодичний десятковий дріб дорівнює звичайному дробові, чисельник якого є число, що стоїть у періоді, а знаменник число, записане стількома дев’ятками, скільки цифр у періоді.
Приклади. 1) 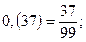 2)
2) 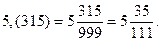
Мішаний періодичний десятковий дріб дорівнює звичайному дробові, чисельником якого є різниця між числом, що стоїть до періоду і в періоді, і числом, що стоїть до періоду, а знаменником — число, записане стількома дев’ятками, скільки цифр у періоді, і з стількома нулями на кінці, скільки цифр між комою і періодом.
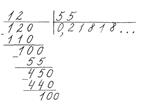 Приклади. 1.
Приклади. 1. 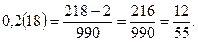
Перевірка.
2. 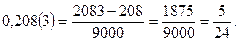
Практично досить часто використовують десяткові дроби із сталим знаменником 100. Такі дроби легко порівнювати між собою, бо не треба попередньо зводити їх до спільного знаменника. Ці дроби, як відомо, називають процентами.
Процент — одна сота частина числа або одиниці (назва походить від двох латинських слів «рrо сеntum» — «від ста» — застаріла назва «відсоток»).
