Синтаксичний аналіз в мовних процесорах

Для визначення синтаксичної компоненти мови програмування використовують контекстно-вільні граматики (КС-граматики). На відміну від скінчено-автоматних граматик потужність класу КС-граматик достатня, щоб визначити майже всі так звані синтаксичні властивості мов програмування. Якщо цього недостатньо, то розглядають деякі спрощення у граматиках типу 2 або параметричні КС-граматики.

Звичайно, із синтаксичною компонентою мови програмування пов'язана семантична компонента. Тоді, якщо ми говоримо про семантику мови програмування, ми вимагаємо семантичної однозначності для кожної вірно написаної програми. За аналогією з семантикою, при описі синтаксичної компоненти мови програмування необхідно користуватися однозначними граматиками.

Означення. Граматика G називається неоднозначною, якщо існує декілька варіантів виводу 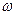в G ( ).

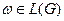Приклад. Розглянемо таку граматику 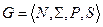зі схемою Р.

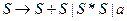
Покажемо, що для ланцюжка 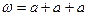існує щонайменше два варіанти виводу:

1.

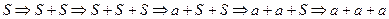
2.

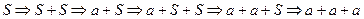
В теорії граматик розглядається декілька стратегій виведення ланцюжка 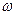в G. Визначимо дві стратегії, які будуть використані в подальшому.

Лівостороння стратегія виводу ланцюжка 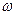в G — це послідовність кроків безпосереднього виводу, при якій на кожному кроку до уваги береться перший зліва направо нетермінал. Правостороння стратегія виводу 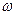в G протилежна лівосторонній стратегії. З виводом 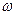в G пов'язане синтаксичне дерево, яке визначає синтаксичну структуру програми.

Означення. Синтаксичне дерево виводу 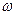в G — це впорядковане дерево, корінь котрого позначено аксіомою, в проміжних вершинах знаходяться нетермінали, а на кроні — елементи з 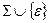. Побудова синтаксичного дерева виведення 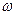в G виконується покроково з урахуванням стратегії виводу 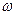в G.

Алгоритм. Побудова синтаксичного дерева ланцюжка 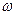в граматиці G з урахуванням лівосторонньої стратегії виводу:

П₁. Будуємо корінь дерева та позначимо його аксіомою S.

П₂. В схемі P граматики G візьмемо правило виду 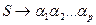, де 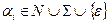. Та побудуємо дерево висоти 1 (Мал. 1).

П_і. На кроні дерева, побудованого на попередньому кроку, візьмемо перший зліва направо нетермінал. Нехай це буде 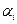. Тоді в схемі P виберемо правило виду 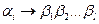, де 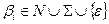та побудуємо наступне дерево (Мал. 2).

S

… …..

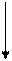
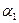
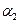
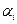
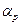Мал. 1.

Пункт П_і виконувати доти, доки на кроні дерева будуть елементи з .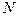

Відмітимо очевидні факти, що випливають з побудови синтаксичного дерева:

- крона дерева, зображеного на мал. 2 наступна 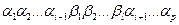. Ланцюжок з крони 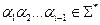- це термінальний ланцюжок.

- для однозначної граматики G існує лише одне синтаксичне дерево виводу 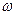в G.

S

… …..

……….

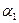
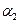
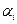
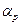
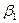
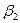
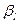
Мал. 2.

Означення. Будемо говорити, що ланцюжок 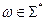, побудований на основі граматики 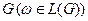проаналізований, якщо відоме одне з його дерев виводу. Зафіксуємо послідовність номерів правил, які були використані під час побудови синтаксичного дерева виводу 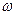в G з урахуванням стратегії виводу.

Означення. Лівостороннім аналізом 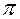ланцюжка 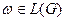будемо називати послідовність номерів правил, які були використані при лівосторонньому виводі 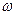в G.

Приклад: Для граматики 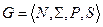зі схемою Р

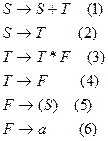
для ланцюжка 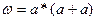побудуємо лівосторонній аналіз :

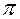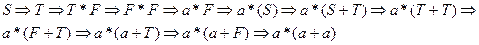
З наведеного вище виводу ланцюжка 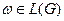лівосторонній аналіз 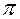буде: 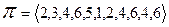, а синтаксичне дерево виводу 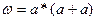зображено на Мал. 4.

Нехай 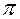лівосторонній аналіз ланцюжка 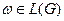. Знаючи 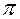досить легко побудувати (відтворити) синтаксичне дерево. Відтворення (синтез) синтаксичного дерева можна виконати, скориставшись однією з стратегій синтаксичного аналізу:

- стратегія "зверху донизу";

- стратегія "знизу вгору".

S

T

T * F

F ( S )

a S + T

T F

F a

a

Мал. 4

Стратегія синтаксичного аналізу "зверху донизу" – це побудова синтаксичного дерева крок за кроком починаючи від кореня до крони.

Алгоритм 2. Синтез синтаксичного дерева на основі лівостороннього аналізу 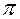ланцюжка .

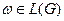П₀: Побудуємо корінь дерева та позначимо його аксіомою S. Тоді, якщ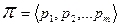о , то

П₁: Побудуємо дерево висоти один, взявши зі схеми Р правило з номером р₁ виду 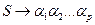(Мал. 5):

S

… …..

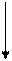
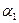
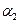
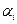
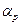
Мал. 5.

П_і: На кроні дерева, отриманого на попередньому кроку, візьмемо перший зліва направо нетермінал (нехай це буде нетермінал 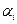) та правило з номером 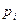виду: 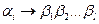та побудуємо нове дерево. Даний пункт виконувати доти, доки не переглянемо всі елементи з .

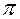Сформулюємо декілька проблем для стратегії аналізу "зверху донизу":

- у загальному випадку у класі КС-граматик існує проблема неоднозначності (недетермінізму) виводу 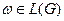. Як приклад можемо розглянути граматику з "циклами". Це така граматика, у якої в схемі 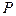існує така послідовність правил за участю нетермінала 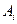, що:

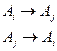, де 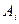— будь-який нетермінал граматики .

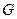- як наслідок з попереднього пункту, граматики з ліворекурсивним нетерміналом для стратегії аналізу "зверху донизу" недопустимі.

- існують підкласи класу КС-граматик, які природно забезпечують стратегію аналізу "зверху донизу". Один з таких підкласів — це LL(k)-граматики, які забезпечують синтаксичний аналіз ланцюжка 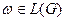за час 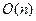, де 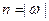, та при цьому є однозначним.

Магазинні автомати

Означення. Магазинний автомат 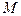— це сімка ,

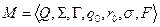де: 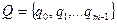— множина станів магазинного автомату;

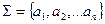— основний алфавіт;

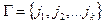— допоміжний алфавіт (алфавіт магазина);

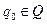— початковий стан магазинного автомату;

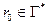— початковий вміст магазину;

;

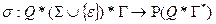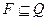— множина заключних станів автомата .

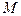Поточний стан магазинного автомата 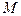описується конфігурацією. Конфігурація магазинного автомата 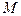— це трійка 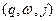, де 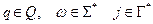. Серед конфігурацій магазинного автомата 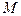виділимо дві:

- початкова конфігурація 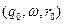, де 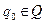, 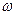— вхідне слово ( ),

;

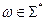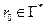- заключна конфігурація 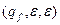, 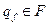. В загальній теорії магазинних автоматів іноді як заключну конфігурацію розглядають 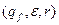, де 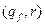- фіксована пара. Легко довести, що визначення заключної конфігурації виду 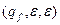не зменшує потужності класу магазинних автоматів.

Такт роботи (позначається ╞═ ) магазинного автомата 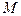— це перехід від однієї конфігурації до іншої, а точніше:

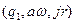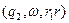╞═ при умові, що .

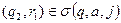Робота магазинного автомата 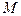(позначається ╞═^*) — це послідовність тактів роботи, а точніше: 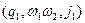╞═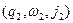^* тоді і тільки тоді, коли ╞═ , ╞═ ,…, ╞═ .

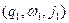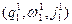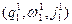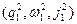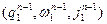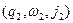Операції ╞═ та ╞═^* можна трактувати як бінарні відношення на відповідних кортежах. Тоді робота магазинного автомата 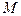— це рефлексивно-транзитивне замикання бінарного відношення ╞═.

Означення. Мова, яку розпізнає магазинний автомат 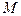(позначається 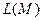) - це множина ланцюжків, які задовольняють умові:

╞═^* .

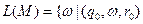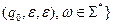Зафіксуємо наступні результати теорії магазинних автоматів:

1. Не існує алгоритму перетворення недетермінованого магазинного автомата у еквівалентний йому детермінований магазинний автомат.

2. Існує алгоритм, який вирішує проблему порожньої множини 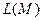для конкретного магазинного автомата.

3. Існує алгоритм, який за час, пропорційний 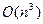перевіряє, чи належить 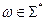мові, яку розпізнає магазинний автомат .

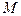4. Клас мов, які розпізнаються магазинними автоматами, співпадає з класом мов, що породжуються КС-граматиками.

На основі сформульованих вище результатів для лівосторонньої стратегії виводу 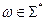в 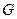запропонуємо наступне твердження: для довільної КС-граматики 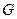можна побудувати магазинний автомат 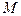такий, що 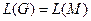. При цьому автомат буде моделювати лівосторонню стратегію виводу 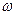в .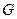

Нехай 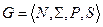— КС-граматика. Побудуємо відповідний МП-автомат :

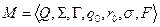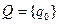- — множину станів автомата складає один стан ;

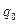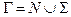- — допоміжний алфавіт;

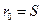- — початковий вміст магазина.

- функцію визначимо так:

- якщо належить 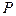, то

.

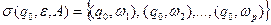- також поповнимо множину значень функції наступними значеннями:

.

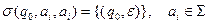Для ланцюжка 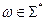, 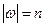покажемо, якщо ми за 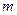кроків безпосереднього виводу 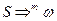, то відповідний автомат за 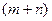кроків допустить 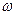. Зробимо перший крок безпосереднього виведення 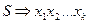тоді МП-автомат з початкової конфігурації 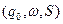перейде в наступну конфігурацію 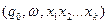. Далі розглянемо наступні ситуації:

- коли 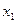— термінал 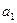(тобто 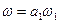), тоді МП-автомат виконає наступний такт: ╞═ ;

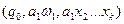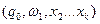- коли 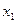— нетермінал, тоді в схемі 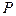граматики 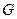виберемо правило виду 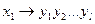, зробимо наступний крок безпосереднього виведення : 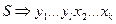. При таких умовах автомат перейде в наступну конфігурацію: ╞═ .

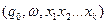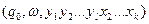Очевидно, якщо ланцюжок 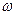виводиться за 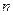кроків, то МП-автомат зробить 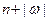кроків та розпізнає 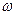. Таким чином, .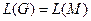