Уточнення кореня методом дотичних (Ньютона)
Якщо метод хорд лінеаризував функцію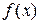 
хордою, метод Ньютона лінеарізує її дотичною в точці a або b (рисунок 24).
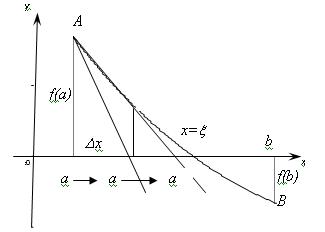
Рисунок 24 – Графічне представлення методу дотичних
При використанні цього методу дуже важливо правильно вибрати точку (a або b) його застосування. Як видно із рисунка 24 дотична з точки А буде наближати точку а до кореня, чого зовсім не можна сказати про дотичну в точці В. Точкою цього процесу потрібно вибрати ту із них, для якої знак функції та знак другої її похідної співпадають: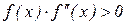 
.
Для виведення ітераційної формули для цього методу розкладено в ряд Тейлора функцію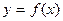 
в точці кореня:
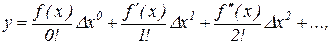де 
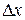– величина на осі ОХ, що наближає початкову точку (a або b) до кореня 
.
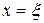Враховуючи ітераційний процес, залишимо в ряду лише два перші члени: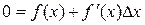 
. Нуль в лівій частині рівності записаний тому, що в точці кореня 
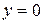. Звідси 
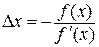. А нове наближення кореня 
.
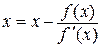Враховуючи знак другої похідної в точках a або b, вибираємо для інтерполяційного процесу по цьому методу одну з формул:
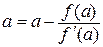або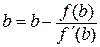 
.
Далі наводимо застосування метода:
