Пример решения контрольной работы №3
Определить вероятность безотказной работы роликоподшипника 2207, нагруженного случайной радиальной силой.
Таблица 1.7 - Исходные данные
| № п/п | Наименование | Значение |
| Коэффициент вариации силы | 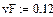 | |
| Частота вращения внутреннего кольца подшипника, об/мин | 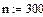 | |
| Требуемый ресурс, ч | 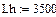 | |
| Среднее значение эквивалентной нагрузки, Н | 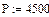 |
Решение:
По каталогу-справочнику [17] определяем 90%-ную динамическую грузоподъемность, Н:
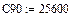
Показатель степени для роликоподшипников
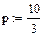
Вычисляем заданный ресурс в миллионах оборотов
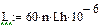
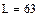
Среднее значение динамической грузоподъемности, Н
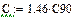
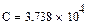
Коэффициент запаса по средним
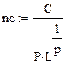
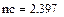
Коэффициент вариации эквивалентной нагрузки принимаем равным коэффициенту вариации внешней нагрузки
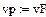
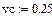
Квантиль нормированного нормального распределения
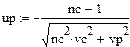
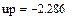
По таблицам нормального распределения (таблица 1.8) в зависимости от полученного значения квантили находим, что вероятность безотказной работы рассчитываемого подшипника равна PL=0.989.
Таблица 1.8 – Нормальное распределение
| Нормальное распределение | Распределение Вейбулла | |||||||
Квантиль 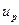 | Вероят- ность безот- ной работы 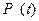 | Квантиль 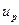 | Вероят- ность безот- ной работы 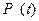 | Параметр формы 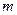 | 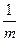 | 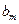 | 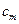 | Коэффи- циент вариации 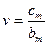 |
| 0,000 | 0,5000 | -2,054 | 0,98 | 0,400 | 2,5 | 3,32 | 10,4 | 3,14 |
| -0,1 | 0,5398 | -2,1 | 0,9821 | 0,417 | 2,4 | 2,98 | 8,74 | 2,93 |
| -0,126 | 0,55 | -2,170 | 0,985 | 0,435 | 2,3 | 2,68 | 7,38 | 2,75 |
| -0,2 | 0,5793 | -2,2 | 0,9861 | 0,455 | 2,2 | 2,42 | 6,22 | 2,57 |
| -0,253 | 0,60 | -2,3 | 0,9893 | 0,476 | 2,1 | 2,20 | 5,27 | 2,40 |
| -0,3 | 0,6179 | -2,326 | 0,99 | 0,500 | 2,0 | 2,00 | 4,47 | 2,24 |
| -0,385 | 0,65 | -2,4 | 0,9918 | 0,526 | 1,9 | 1,83 | 3,81 | 2,08 |
| -0,4 | 0,6554 | -2,409 | 0,992 | 0,556 | 1,8 | 1,68 | 3,26 | 1,94 |
| -0,5 | 0,6915 | -2,5 | 0,9938 | 0,588 | 1,7 | 1,54 | 2,78 | 1,80 |
| -0,524 | 0,70 | -2,576 | 0,995 | 0,625 | 1,6 | 1,43 | 2,39 | 1,67 |
| -0,6 | 0,7257 | -2,6 | 0,9953 | 0,667 | 1,5 | 1,33 | 2,06 | 1,55 |
| -0,674 | 0,75 | -2,652 | 0,996 | 0,714 | 1,4 | 1,24 | 1,78 | 1,43 |
| -0,7 | 0,7580 | -2,7 | 0,9965 | 0,769 | 1,3 | 1,17 | 1,54 | 1,32 |
| -0,8 | 0,7881 | -2,748 | 0,997 | 0,833 | 1,2 | 1,10 | 1,33 | 1,21 |
| -0,842 | 0,80 | -2,8 | 0,9974 | 0,909 | 1,1 | 1,05 | 1,15 | 1,10 |
| -0,9 | 0,8159 | -2,878 | 0,998 | 1,0 | 1,0 | 1,00 | 1,00 | 1,00 |
| -1,0 | 0,8413 | -2,9 | 0,9981 | 1,1 | 0,909 | 0,965 | 0,878 | 0,910 |
| -1,036 | 0,85 | -3,0 | 0,9986 | 1,2 | 0,833 | 0,941 | ||
| -1,1 | 0,8643 | 3,090 | 0,999 | 1,3 | 0,769 | 0,924 | 0,716 | 0,775 |
| -1,2 | 0,8849 | -3,291 | 0,9995 | 1,4 | 0,714 | 0,911 | 0,659 | 0,723 |
| -1,282 | 0,90 | -3,5 | 0,9998 | 1,5 | 0,667 | 0,903 | 0,615 | 0,681 |
| -1,3 | 0,9032 | -3,719 | 0,9999 | 1,6 | 0,625 | 0,897 | 0,574 | 0,640 |
| -1,4 | 0,9192 | 1,7 | 0,588 | 0,892 | 0,540 | 0,605 | ||
| -1,5 | 0,9332 | 1,8 | 0,556 | 0,889 | 0,512 | 0,575 | ||
| -1,6 | 0,9452 | 1,9 | 0,526 | 0,887 | 0,485 | 0,547 | ||
| -1,645 | 0,95 | 2,0 | 0,500 | 0,886 | 0,463 | 0,523 | ||
| -1,7 | 0,9554 | 2,1 | 0,476 | 0,886 | 0,439 | 0,496 | ||
| -1,751 | 0,6 | 2,2 | 0,455 | 0,886 | 0,425 | 0,480 | ||
| -1,8 | 0,9641 | 2,3 | 0,435 | 0,886 | 0,409 | 0,461 | ||
| -1,881 | 0,97 | 2,4 | 0,417 | 0,887 | 0,394 | 0,444 | ||
| -2,0 | 0,9772 | 2,5 | 0,400 | 0,887 | 0,380 | 0,428 |
Примечания:
1. Под t понимается время или другие случайные величины.
2. Для логарифмически нормального распределения