Оценки случайных величин

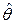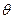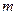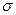Различают точечные и интервальные оценки. Точечная оценка некоторого параметра определяется по результатам выборки одним числом. Для того, чтобы точечная оценка была «хорошей» необходимо, чтобы она была состоятельной, несмещенной, эффективной. Задача оценивания параметров и сводится к нахождению таких функций от выборк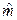и и 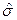, которые могут быть использованы для приближенного определения параметров 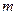и 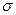. В качестве точечных оценок для 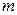и 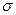нормально распределенной СВ 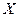( 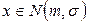) принимаются:

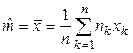(1.2)

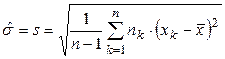(1.3)

Точечные оценки не указывают величины ошибки, которая совершается при замене 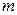и 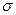их приближенными значениям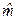и и 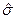. Поэтому иногда выгоднее пользоваться интервальной оценкой, которая определяется двумя числам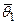и и 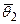– концами интервала, накрывающего оцениваемый параметр 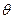с заданной вероятностью (надежностью).

Пусть 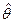– точечная оценка параметра 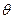. Она тем лучше, чем меньше разность 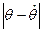. Тогда в качестве характеристики точности оценки можно взять некоторое 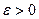такое, что .

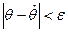Доверительной вероятностью оценки называется вероятность 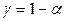выполнения неравенства 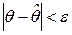. Доверительный интервал – это интервал, который накрывает неизвестный параметр 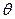с заданной надежностью 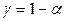. Чем меньше длина доверительного интервала, тем точнее оценка.

При неизвестном 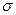доверительный интервал для математического ожидания 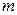СВ 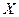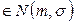имеет вид:

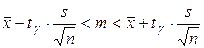, (1.4)

где величина 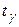определяется по таблицам по заданному уровню значимости 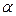(либо надежности 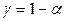) и объему выборки .

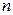Доверительный интервал для 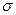задается неравенствами

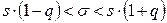, если 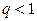, (1.5)

либо

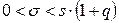, если 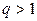. (1.6)

Величина 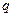определяется по таблице доверительных интервалов для 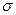по доверительной вероятности 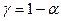и объему выборки .

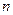Медианой 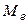называется вариант, который приходится на середину ряда распределения. При вычислении медианы дискретного ряда рассматриваются два случая: объем совокупности четный и нечетный. В первом случае применяется формула 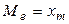, если 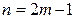( 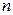– объем совокупности). Если 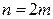, то медиана: .

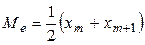Модой 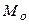называется вариант, который наиболее часто встречается. Мода – это вариант, которому соответствует наибольшая частота или частоты.

Эмпирической функцией распределения СВ 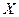называют функцию

,

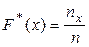где 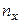– число значений 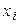меньших, чем ;

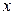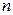– объем выборки.

Эмпирическая функция распределения используется в качестве оценки функции распределения.

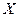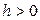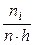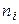Для наглядности данные выборки можно представить графически в виде гистограммы, а также полигона относительных частот. Для построения гистограммы интервал наблюдаемых значений СВ разбивается над подынтервалы равной длины , на каждом из которых строится прямоугольник с высотой , где – число значений СВ 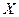из выборки, попадающих в рассматриваемый подынтервал. Ломаная, соединяющая точки пересечения середин подынтервалов с соответствующими высотами 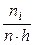, образуют полигон относительных частот.

Если форма гистограммы или полигона относительных частот напоминает кривую Гаусса, то можно выдвинуть гипотезу о нормальном распределении СВ 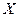. Для проверки того, что СВ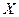 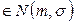можно использовать следующие характеристики: асимметрию 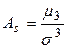и эксцесс 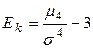, где .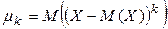

Для нормального распределения 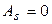, 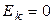. По данным выборки объема 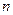можно найти точечные оценк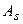и и :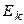

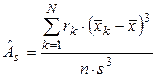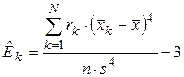, , (1.7)

где 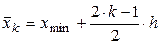, а также средние квадратичные ошибки и их определения

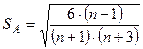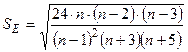; . (1.8)

Гипотеза о нормальности закона распределения СВ 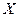выдвигается, есл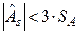и и 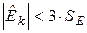. В противном случае она отвергается.

После предварительного выбора закона распределения рекомендуется применять строгие критерии согласия.

1.3. Критерий 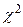-Пирсона

При проверке гипотезы о нормальном распределения СВ 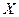с помощью критерия 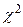-Пирсона поступают следующим образом:

1) вычисляют вероятности 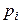попадания СВ 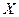в подынтервалы , ;

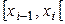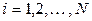2) вычисляют выборочную статистику

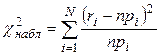; (1.9)

3) сравнивают 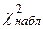с квантилем 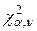, определяемым по таблицам по заданному уровню значимости 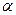и числу степеней свободы 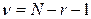, где 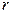– число параметров предполагаемого распределения СВ 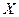. Если 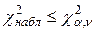, то считают, что нет оснований для отклонения проверяемой гипотезы. В противном случае гипотеза отклоняется.