Способы графического изображения рядов распределения
| Понятие | Характеристика |
| Полигон распределения | Применяется для изображения дискретных рядов распределения. По оси координат по оси абсцисс откладываются варианты (х), по оси ординат – частоты (f). Из точки, соответствующей значению варианты, на оси абсцисс восстанавливается перпендикуляр; на оси ординат из точки соответствующей частоте данной варианты проводится линия параллельная оси абсцисс. На пересечении ее с перпендикуляром отмечается точка, имеющая координаты варианты и частоты. Полученные точки соединяются отрезками прямой. |
| Гистограмма распределения | Интервальный вариационный ряд изображается в виде прямоугольников, построенных на оси (х). Ширина прямоугольников равна интервалу, а высота пропорциональна соответствующей частоте. Если середины верхних сторон прямоугольников соединить прямыми, то получится полигон распределения |
| Кумулята | Строится по накопленным (кумулятивным) частотам, которые наносятся на перпендикулярную ось графика. На оси (у) откладываются либо дискретные значения признака, либо интервалы. В этом случае накопленная частота соотносится с верхней границей интервала. Полученные точки соединяются прямыми, образуя ломаную линию, которая возрастает от нуля до высоты, равной общей сумме частот. |
Темы Средние величины и показатели вариации(задачи 2, 3 и 4)
Виды средних величин
| Вид средней | Показатель степени | Формулы расчета | |
| простая | взвешенная | ||
| Средняя арифметическая | 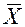 = = 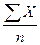 | 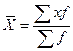 | |
| Средняя гармоническая | -1 | 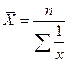  | 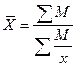 ;где М= x*f ;где М= x*f |
| Средняя геометрическая | 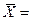 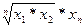 | 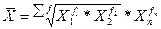 | |
| Средняя квадратическая |  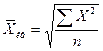 | 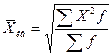 |
Модa и Медиана
.
Мода- значение признака (варианты), наиболее часто встречающегося в данной совокупности, т.е. варианта, имеющая наибольшую частоту.
1. Пример определение Моды дискретного ряда на примере:
| Х | |||||||||
| f |
Для определения Моды необходимо найти варианту имеющую наибольшие частоты
Мо = 15, так как f= 28 = max
2. Определение моды интервального ряда несколько сложнее.
Сначала определяем модальный интервал.
Модальным является интервал, имеющий наибольшую частоту.
Затем значение моды определяется по следующей формуле:
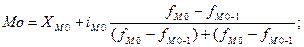
Где: Хмо –нижняя граница модального интервала; iмо- величина модального интервала; fMo , fMo-1, fMo+1 – частототы модального, предмодального и послемодального интервалов.
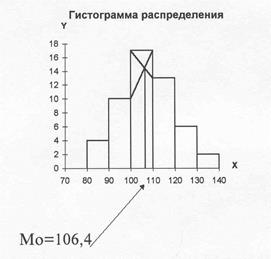
Определение Моды графическим путем. Для этого строят гистограмму распределения и в интервале, имеющим максимальную частоту проводя диагонали. Из точки пересечения диагоналей опускают перпендикуляр на ось Х. Это и будет значение Моды.
Медиана - это значение признака, находящегося в середине ранжированного вариационного ряда.
Определение Медианы дискретного ряда.
Исходные данные
| Х | f | Sf (накопленные частоты) |
1. Для нахождения Ме сначала определяют № медианы по формуле:
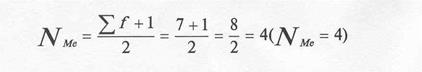
2. После этого определяют накопление частоты.
После определения накопленных частот находят значение Медианы следующим образом:
а) сравниваем номер Me с накопленными частотами. Медианой будет являться значение признака накопления частоты, которого в точности совпадает с номером медианы или является к нему ближайшей большей.
Медиана интервального ряда
| Х | f | Sf |
| 6-12 | ||
| 12-18 | ||
| 18-24 | ||
| 24-30 | ||
| 30-36 | ||
| Sf=30 |
1. Сначала определяется номер Медианы

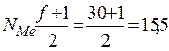
2. Затем рассчитываются накопленные частоты ( гр. 3 в таблице исходных данных)
3. Определяется Медианный интервал :
Медианным - является интервал, накопленная частота которого в точности совпадает с номеров Медианы или является к нему ближайшим большим.
В примере ближайшая большая к номеру медианы накопленная частота соответствует интервалу 18-24.
4. Определяется значение Медианы по формуле:
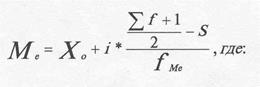

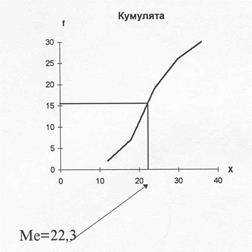
Графически медиану можно определить на основе построения кумуляты распределения.
Показатели вариации
| Показатель вариации | Формула |
| Размах вариации | R 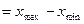 |
| Среднее линейное отклонение | 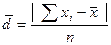 или или 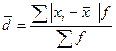  |
| Дисперсия признака | 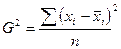 или G или G 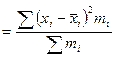 |
| Среднее квадратическое отклонение | 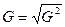 |
| Коэффициент осцилляции | 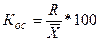 |
| Линейный коэффициент вариации | 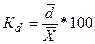 |
| Коэффициент вариации | 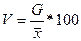 |
Тема: Ряда динамики (задача 6)
