Смешанное произведение векторов и его геометрический смысл

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись 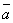, , 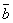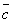означает, что вектор 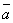считается первым, 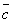- вторым, 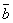- третьим.

Тройка некомпланарных векторов 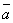, , 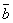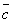называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы 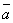, , 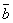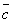расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов 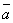, , 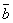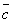называется число, равное векторному произведению 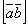, умноженному скалярно на вектор 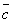, то есть .

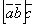Имеет место тождество 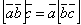, ввиду чего для обозначения смешанного произведения 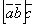употребляется более простой символ 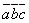. Таким образом,

, .

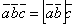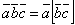Смешанное произведение 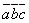равно объему параллелепипеда, построенного на векторах 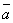, , 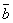, 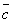взятого со знаком плюс, если тройка 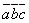правая, и со знаком минус, если эта тройка левая. Если векторы 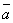, , 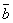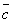компланарны (и только в этом случае), смешанное произведение 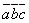равно нулю; иначе говоря, равенство

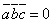
есть необходимое и достаточное условие компланарности векторов , , .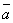

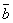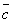Применение смешанного произведения

Применяется для вычисления объемов.

 Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .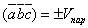

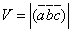Таким образом, и .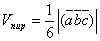

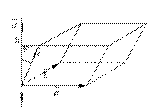
Доказательство. Отложим векторы 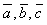от общего начала и построим на них параллелепипед. Обозначим 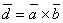и заметим, что 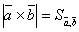. По определению скалярного произведения

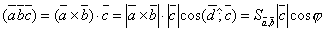. Предполагая, что 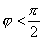и обозначив через h высоту параллелепипеда, находим .

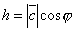Таким образом, при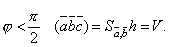

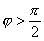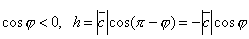Если же , то и 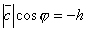. Следовательно, .

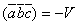Объединяя оба эти случая, получаем 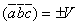или .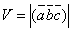

Из доказательства этого свойства в частности следует, что если тройка векторов 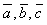правая, то смешанное произведение 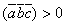, а если 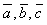– левая, то .

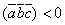 Для любых векторов 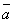, , 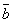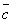справедливо равенство

.

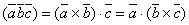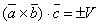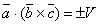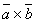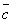Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами и 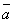и и 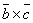одновременно острые или тупые.

 При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение 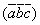, то, например, 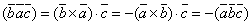или

.

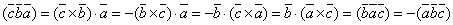Вычисление смешанного произведения в координатах. Признак компланарности трех векторов

Если векторы 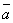, , 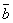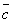заданы своими координатами:

, ,

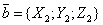
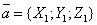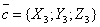
то смешанное произведение 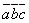определяется формулой

.

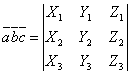Напомним, что система координатных осей предполагается правой (вместе с тем является правой и тройка векторов , , ).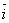

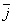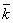Свойства смешанного произведения.

1 Кососимметричность. При перестановке любых двух векторов смешанное произведение меняет знак:

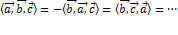
Полилинейность, т.е. линейность по каждому сомножителю:

2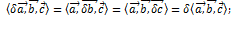

3 ,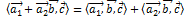

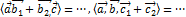
Эти свойства следуют из соответствующих свойств определителя, так как смешанное произведение в координатах выражается в виде определителя.

 Смешанное произведение 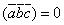тогда и только тогда, когда один из сомножителей равен нулю или векторы 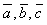– компланарны.

Доказательство.

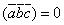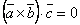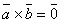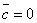1. Предположим, что , т.е. , тогда или или .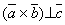

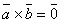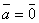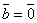Если , то или или 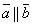. Поэтому 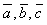– компланарны.

Если 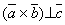, то 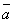, , 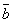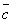- компланарны.

1. Пусть векторы 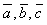– компланарны и α – плоскость, которой они параллельны , т. е. 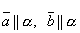и 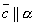. Тогда 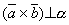, а значит 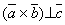, поэтому 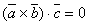или .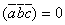

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора 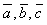образуют базис в пространстве, если .

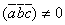Если векторы заданы в координатной форме 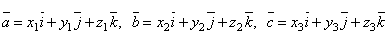, то можно показать, что их смешанное произведение находится по формуле:

.

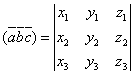Т. о., смешанное произведение 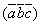равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.