Ауыстыру және алмастыру
 , мұндағы
, мұндағы  , қайтымды бейнелеуі
, қайтымды бейнелеуі 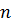 дәрежелі ауыстыру (кейде сондай-ақ алмастыру) деп аталады.
дәрежелі ауыстыру (кейде сондай-ақ алмастыру) деп аталады.  ауыстыруын бегілеу үшін көбінесе
ауыстыруын бегілеу үшін көбінесе

кестесі қолданылады, мұнда  сандары
сандары  сандарының ауыстыруын құрады (бұл
сандарының ауыстыруын құрады (бұл  бейнелеуінің қайтымдылығымен пара-пар).
бейнелеуінің қайтымдылығымен пара-пар).
 ауыстыруының көбейтіндісін
ауыстыруының көбейтіндісін  бейнелеулерінің тізбектей орындалуымен (композициямен) алынатын бейнелеу ретінде анықтайық:
бейнелеулерінің тізбектей орындалуымен (композициямен) алынатын бейнелеу ретінде анықтайық:

Бұл барлық  дәрежелі ауыстырулар жиынындағы алгебралық амал болып табылады, осыған қатысты ол группа құрайды. Ассоциативтілігі айқын (бейнелеудің композициясы бұл қасиетке әрқашанда ие болады). Мұнда бірлік элементтің рөлін
дәрежелі ауыстырулар жиынындағы алгебралық амал болып табылады, осыған қатысты ол группа құрайды. Ассоциативтілігі айқын (бейнелеудің композициясы бұл қасиетке әрқашанда ие болады). Мұнда бірлік элементтің рөлін

теңбе-тең бейнелеуі атқарады, ал 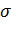 элементіне кері элемент
элементіне кері элемент  кері бейнелеуі болады.
кері бейнелеуі болады.
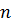 дәрежелі ауыстырулар группасы
дәрежелі ауыстырулар группасы 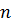 дәрежелі симметриялық группа деп аталады және
дәрежелі симметриялық группа деп аталады және  деп белгіленеді. Бұл ақырлы группалардың (элементтер саны ақырлы болатын группалар; сонымен қатар элементтер саны группаның реті деп аталады) ең маңызды мысалдарының бірі.
деп белгіленеді. Бұл ақырлы группалардың (элементтер саны ақырлы болатын группалар; сонымен қатар элементтер саны группаның реті деп аталады) ең маңызды мысалдарының бірі.  группасының реті
группасының реті  тең болады.
тең болады.
Симметриялық группа түсінігі симметриялық функциялар түсінігінің анықтамасынан шыққан. Симметриялық функция деп өзінің аргументінің кез келген ауыстыруына қатысты инвариантты болатын  функциясын айтады:
функциясын айтады:

Симметриялық функцияға мысалы мынадай (  сандық параметрімен анықталатын) функция жатады:
сандық параметрімен анықталатын) функция жатады:

3.3 Циклдар және транспозициялар (орын ауыстырулар)
Егер
(1) 
(2) 
болатындай  қос-қостан әр түрлі
қос-қостан әр түрлі  нөмірлері бар болса, онда
нөмірлері бар болса, онда  ауыстыруы ұзындығы
ауыстыруы ұзындығы  -ға тең цикл деп аталады.
-ға тең цикл деп аталады.
 циклын
циклын  деп белгілейді. Ұзындығы 2-ге тең цикл транспозиция (орын ауыстыру) деп аталады.
деп белгілейді. Ұзындығы 2-ге тең цикл транспозиция (орын ауыстыру) деп аталады.
 және
және  циклдары тәуелсіз деп аталады, егер
циклдары тәуелсіз деп аталады, егер  болса.
болса.
Қасиеттері.
(1) Кез келген тәуелсіз  циклдары коммутативті:
циклдары коммутативті:  ;
;
(2) Кез келген  ауыстыруы тәуелсіз циклдардың көбейтіндісі түріне көбейткіштердің ретіне дейінгі дәлдікпен бірмәнді келтірімді.
ауыстыруы тәуелсіз циклдардың көбейтіндісі түріне көбейткіштердің ретіне дейінгі дәлдікпен бірмәнді келтірімді.
(3) Ұзындығы 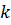 -ға тең кез келген цикл
-ға тең кез келген цикл  транспозиция түріне келтірімді.
транспозиция түріне келтірімді.
(4) Кез келген ауыстыру транспозициялардың көбейтіндісі түріне келтірімді.
Дәлелдеу. (1) тұжырымды дәлелдеу үшін  және
және  тәуелсіз циклдар жағдайында мынаны табамыз:
тәуелсіз циклдар жағдайында мынаны табамыз:
 ,
,  болғанда,
болғанда,
 ,
,  болғанда,
болғанда,
 ,
,  болғанда.
болғанда.
(2)-ні дәлелдеу үшін кез келген 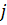 нөмірін алып,
нөмірін алып,  нөмірлер тізбегін қарастырайық. Тек қана
нөмірлер тізбегін қарастырайық. Тек қана 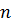 әр түрлі мәндер бар, сондықтан да қандай да бір
әр түрлі мәндер бар, сондықтан да қандай да бір  үшін
үшін  болу керек, бұдан
болу керек, бұдан  аламыз. Айталық,
аламыз. Айталық, 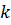 -
-  болатындай ең кіші нөмір болсын. Онда мынадай цикл аламыз:
болатындай ең кіші нөмір болсын. Онда мынадай цикл аламыз:

ал бұған  болғанда
болғанда  болады. Енді
болады. Енді  болсын, онда
болсын, онда

түріндегі түрлендіру орындалатын  циклын құрамыз. Осылай жалғастыра берсек, нәтижесінде мынадай теңбе-тең ауыстыруға келеміз:
циклын құрамыз. Осылай жалғастыра берсек, нәтижесінде мынадай теңбе-тең ауыстыруға келеміз:

бұдан

 циклдары құрылуы бойынша тәуелсіз.
циклдары құрылуы бойынша тәуелсіз.
(3)-ші тұжырым тексеру арқылы дәлелденеді, мысалы
 .
.
(4)-ші тұжырым (2) мен (3)-тен шығады.
