Приведение масс и моментов инерции.

Лекция №15

Исследование движения машинного агрегата.

В общем случае машинный агрегат состоит из двигателя, передаточного механизма (например, редуктор) и исполнительного механизма (рис.15.1).

Рис.15.1

Предполагаются уже известными размеры звеньев исполнительного льного механизма. Проведён геометро- кинематический анализ, известны аналоги скоростей, ускорений звеньев , массы и моменты инерции звеньев, средняя частота вращения ведущего звена исполнительного механизма.

Силы и пары сил, приложенные к машине можно разделить на следующие группы:

1. Движущие силы и моменты. Их направление совпадает с направлением движения звена, к которому они приложены. Они совершают за цикл положительную работу. Их величина определяется в процессе динамического анализа. При этом они могут приниматься постоянными или зависящими от скорости или перемещения.

2. Силы и моменты полезного сопротивления. Их направление противоположно направлению движения звена, к которому приложены. Они совершают за цикл отрицательную работу. Их величина должна быть задана в виде графиков или механических характеристик.

3. Силы трения в кинематических парах. Производят отрицательную работу. Их конечное действие можно учитывать через к.п.д. в кинематических парах.

4. Силы тяжести подвижных звеньев. На отдельных участках движения эти силы могут совершать как положительную, так и отрицательную работу. Однако за полный кинематический цикл работа сил тяжести равна нулю.

Динамическая модель машины.

Рассматривается машина, состоящая из исполнительного механизма ИМ (рис.15.1) и привода, включающего в себя двигатель Д и передачу П. При использовании в приводе электродвигателя ведущему звену 1 исполнительного механизма сообщается вращательное движение. Если механизм жесткозвенный и имеет одну степень свободы, то движение всех звеньев определяется движением одного ведущего звена. Таким образом, в качестве динамической модели машины может быть принято вращающееся звено 1 (рис.15.2), являющееся ведущим звеном исполнительного механизма. Положение его определяется углом поворота φ, а движение – угловой скоростью ω и угловым ускорением ε. При этом все силы, действующие на звенья машины, заменяются приведенным моментом М_пр, а массы и моменты инерции всех звеньев заменяются приведенным моментом инерции J_пр.

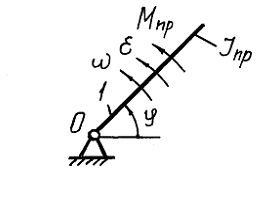Рис.15.2

Приведение сил.

Операция приведения осуществляется для каждой силы F_iили момента M_i , действующих в машине, а затем приведенные моменты М_прi cуммируются. При этом используется условие равенства элементарныхработ или мощностей. Если приводится сила F_i , то

M_{ПР i} ω= F_i V_i соs α_i ,

где V_i – скорость точки приложения силы F_i, a_i - угол между векторами F_i и V_i. Откуда

M_{ПР i} =( F_i V_i соs α_i)/ω = F_i S_i ¢ соs α_i (15.1)

Здесь S _i¢ - аналог скорости точки приложения силы F _i .

Если приводится момент М _i, то М_{ПР i} ω = M _i w _i ,

где w_i – угловая скорость звена, к которому приложен момент М_i. Тогда

М_{ПР i} =( M_i w_i) / w . (15.2)

Общий приведенный момент

М_ПР = 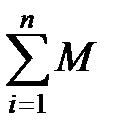_{ПР i}.

В расчет принимаются только внешние силы (движущие, полезного сопротивления, тяжести). Из анализа формул (15.1) и (15.2) следует, что М_ПР,в общем случае, является переменным, зависящим от положения механизма и скорости:

М_пр = М_пр(j, w). (Зависимость от скорости дает движущий момент).

В качестве примера рассмотрим приведение сил, действующих на ползун 3 кривошипно-ползунного механизма (рис.15.3).

Расположение механизма определяется углом β между положительным направлением оси X и вектором силы тяжести (угол отсчитывается от оси X против часовой стрелки). Угол φ отсчитывается от положения ОА₀ кривошипа, в котором ползун занимает крайнее дальнее положение. Отсчёт угла φ, направление угловой скорости ω против часовой стрелки считаются положительными.

Считаем известными длину кривошипа r = ОА, длину шатуна l = АВ, , массу ползуна m₃ (массы кривошипа и шатуна не учитываем), силу полезного сопротивления Р.

Предварительно должен быть выполнен кинематический расчёт и определены аналоги скоростей ползуна S′.

Определим приведённый момент М_с силы сопротивления Р на ползуне ( с учётом его силы тяжести G₃).

Знак силы Р определяется её направлением относительно оси X. Само направление силы сопротивления противоположно скорости ползуна. Используя зависимость (15.1), получим

М_с = (Р + G₃ cos β) ∙ S′. (15.3)

Здесь G₃ = 9,81∙ m₃.

Все значения Р, S′подставляются вформулу (15.3) с учётом знаков. Знак силы G₃ учтён в формуле (15.3), так как сила тяжести всегда направлена вниз.

Рис.15.3

Приведение масс и моментов инерции.

Операция приведения осуществляется для каждого звена, а затем приведенные моменты инерции cсуммируются. При этом используетсяусловие равенства кинетических энергий. Расчетные формулы зависят от вида движения звена (в плоских механизмах три варианта). Если звено совершает поступательное движение, то

= ,

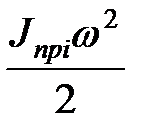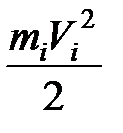где m_i – масса звена, V_i – скорость звена. Откуда

J_{пр i} =m _i ( 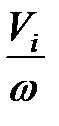)²=m_i(S¢ _i )². (15.4)

Если звено совершает вращательное движение, то

= ,

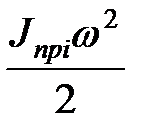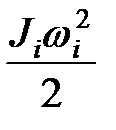где J_i – момент инерции звена относительно оси вращения,

w_i – угловая скорость звена.

Тогда J_{пр i} =J_i ( 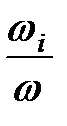)². (15.5)

Если звено совершает сложно-плоское движение, то получим

= + ,

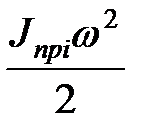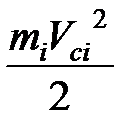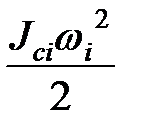где V_ci – скорость центра масс звена, J_ci– момент инерции звена относительно центра масс. Поэтому

J_{пр i} = m_i ( 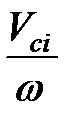)² + J_ci ( 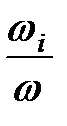)².(15.6)

Общий приведенный момент инерции J_пр = _{ПР i}.

Из анализа формул (15.4), (15.5), (15.6) следует, что J_ПР в общем случае является переменной величиной, зависящей от положения механизма.

Можно записать J_пр = J_c+J_v : (15.7)

здесь J_c – постоянная часть приведённого момента инерции (от звеньев, совершающих вращательное движение);

J_v – переменная часть приведённого момента инерции (от звеньев, совершающих возвратно-поступательное, качательное и сложно-плоское движение ).